O que é uma variável confusa? (definição e #038; exemplo)

Em qualquer experimento, existem duas variáveis principais:

A variável independente: a variável que um experimentador modifica ou controla para poder observar os efeitos na variável dependente.

A variável dependente: a variável medida em um experimento que é “dependente” da variável independente.

Os pesquisadores estão frequentemente interessados em compreender como as mudanças na variável independente afetam a variável dependente.

Porém, às vezes acontece que uma terceira variável não é levada em consideração e pode afetar a relação entre as duas variáveis estudadas.

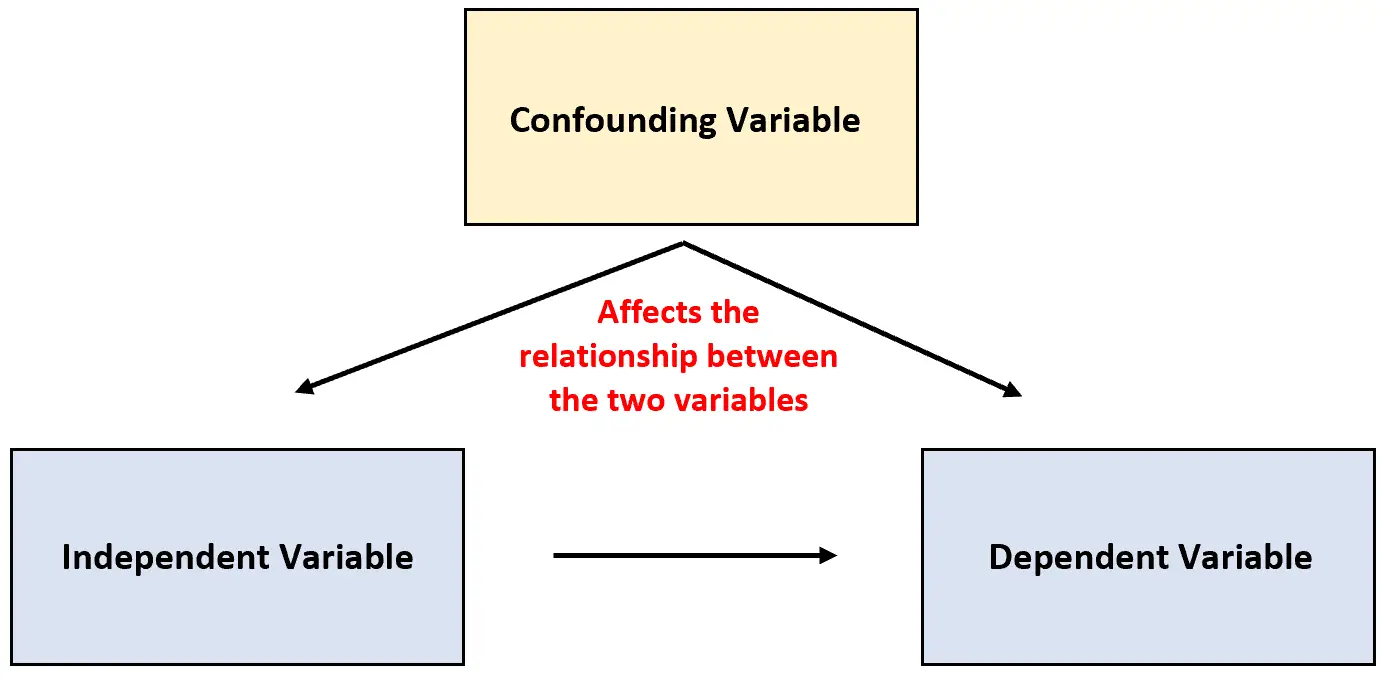
Esse tipo de variável é conhecida como variável de confusão e pode confundir os resultados de um estudo e fazer parecer que existe algum tipo de relação de causa e efeito entre duas variáveis que na verdade não existe.

Variável de confusão: uma variável que não está incluída em um experimento, mas afeta a relação entre as duas variáveis em um experimento.

Este tipo de variável pode confundir os resultados de um experimento e levar a resultados não confiáveis.

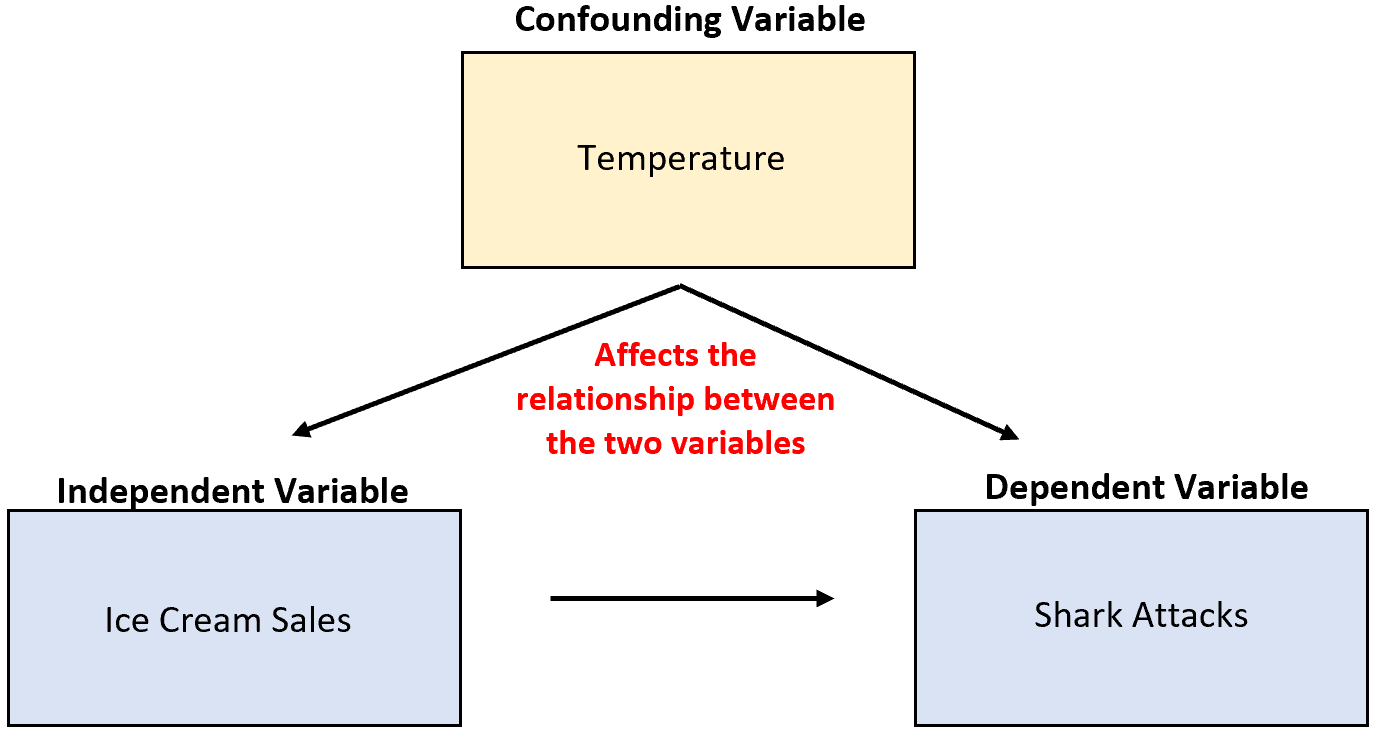
Por exemplo, suponha que um pesquisador colete dados sobre vendas de sorvetes e ataques de tubarões e descubra que as duas variáveis estão altamente correlacionadas. Isso significa que o aumento das vendas de sorvetes está causando mais ataques de tubarões?

É improvável. A causa mais provável é a confusa temperatura variável. Quando está mais quente lá fora, mais pessoas compram sorvete e mais pessoas vão para o mar.

Requisitos para variáveis confusas

Para que uma variável seja uma variável confusa, ela deve atender aos seguintes requisitos:

1. Deve estar correlacionado com a variável independente.

No exemplo anterior, a temperatura foi correlacionada com a variável independente venda de sorvetes. Em particular, temperaturas mais quentes estão associadas a vendas mais elevadas de gelados e temperaturas mais frias a vendas mais baixas.

2. Deve haver relação causal com a variável dependente.

No exemplo anterior, a temperatura teve um efeito causal direto no número de ataques de tubarões. Em particular, as temperaturas mais altas levam mais pessoas ao oceano, o que aumenta diretamente a probabilidade de ataques de tubarões.

Por que as variáveis confusas são problemáticas?

Variáveis confusas são problemáticas por dois motivos:

1. Variáveis confusas podem fazer parecer que existem relações de causa e efeito, quando na verdade não existem.

No nosso exemplo anterior, a variável confusa temperatura fez parecer que havia uma relação causal entre as vendas de gelados e os ataques de tubarões.

Porém, sabemos que a venda de sorvete não provoca ataques de tubarões. A variável confusa da temperatura faz com que pareça assim.

2. Variáveis confusas podem obscurecer a verdadeira relação de causa e efeito entre as variáveis.

Suponha que estejamos estudando a capacidade do exercício de reduzir a pressão arterial. Uma potencial variável de confusão é o peso inicial, que está correlacionado com o exercício e tem um efeito causal direto na pressão arterial.

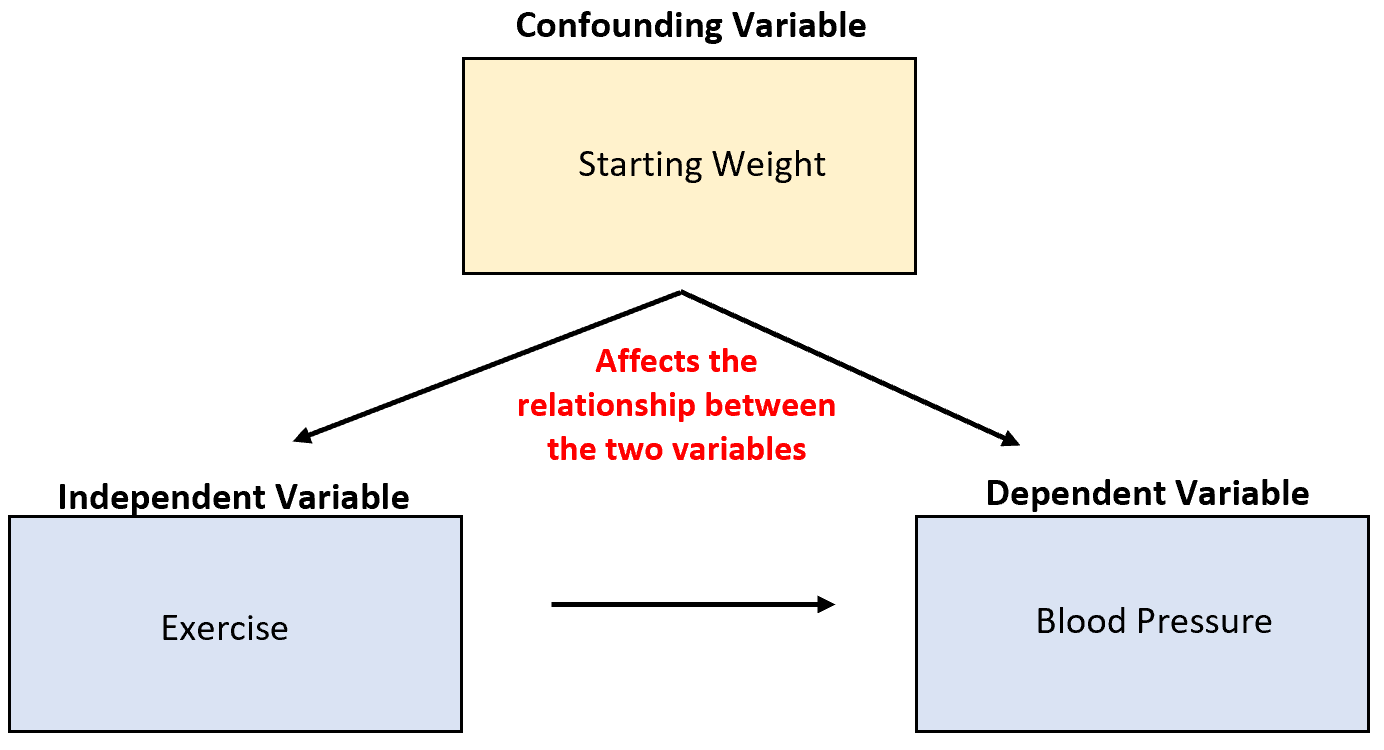
Embora o aumento da atividade física possa levar à redução da pressão arterial, o peso inicial de um indivíduo também tem um grande impacto na relação entre essas duas variáveis.

Variáveis de confusão e validade interna

Em termos técnicos, as variáveis de confusão afetam a validade interna de um estudo, que se refere à validade de atribuir quaisquer alterações na variável dependente a alterações na variável independente.

Quando estão presentes variáveis de confusão, nem sempre podemos dizer com certeza que as alterações que observamos na variável dependente são um resultado direto de alterações na variável independente.

Como reduzir o efeito de variáveis confusas

Existem várias maneiras de reduzir o efeito de variáveis confusas, incluindo os seguintes métodos:

1. Alocação aleatória

A atribuição aleatória refere-se ao processo de atribuição aleatória de indivíduos em um estudo a um grupo de tratamento ou grupo de controle.

Por exemplo, digamos que queremos estudar o efeito de uma nova pílula na pressão arterial. Se recrutarmos 100 pessoas para participarem no estudo, poderíamos usar um gerador de números aleatórios para atribuir aleatoriamente 50 pessoas a um grupo de controle (sem pílula) e 50 pessoas a um grupo de tratamento (nova pílula).

Ao utilizar a atribuição aleatória, aumentamos a probabilidade de os dois grupos terem características aproximadamente semelhantes, o que significa que quaisquer diferenças observadas entre os dois grupos podem ser atribuídas ao tratamento.

Isto significa que o estudo deve ter validade interna : é válido atribuir quaisquer diferenças na pressão arterial entre os grupos à própria pílula, em oposição às diferenças entre os indivíduos dos grupos.

2. Bloqueio

Bloqueio refere-se à prática de dividir os indivíduos de um estudo em “blocos” com base em um determinado valor de uma variável de confusão, a fim de eliminar o efeito da variável de confusão.

Por exemplo, suponha que os pesquisadores queiram compreender o efeito de uma nova dieta na perda de peso. A variável independente é a nova dieta e a variável dependente é a quantidade de perda de peso.

No entanto, uma variável confusa que pode causar variação na perda de peso é o sexo . É provável que o sexo de um indivíduo tenha impacto na quantidade de peso que perde, quer a nova dieta funcione ou não.

Uma maneira de resolver esse problema é colocar os indivíduos em um de dois blocos:

• Macho
• Fêmea

Então, dentro de cada bloco, atribuiríamos aleatoriamente indivíduos a um de dois tratamentos:

• Uma nova dieta
• Uma dieta padrão

Ao fazer isso, a variação dentro de cada bloco seria muito menor do que a variação entre todos os indivíduos e seríamos capazes de entender melhor como a nova dieta afeta a perda de peso e ao mesmo tempo controlar o sexo.

3. Correspondência

Umprojeto de pares combinados é um tipo de projeto experimental no qual “combinamos” indivíduos com base nos valores de possíveis variáveis de confusão.

Por exemplo, suponha que os pesquisadores queiram saber como uma nova dieta afeta a perda de peso em comparação com uma dieta padrão. Duas variáveis potencialmente confusas nesta situação são a idade e o género .

Para dar conta disso, recrute 100 pesquisadores para pesquisadores e agrupe-os em 50 pares com base em idade e sexo. Por exemplo:

• Um homem de 25 anos será comparado com outro homem de 25 anos, uma vez que “combinam” em termos de idade e sexo.
• Uma mulher de 30 anos será combinada com outra mulher de 30 anos, uma vez que também são iguais em termos de idade e sexo, etc.

Então, dentro de cada par, um sujeito será designado aleatoriamente para seguir a nova dieta por 30 dias e o outro sujeito será designado para seguir a dieta padrão por 30 dias.

Ao final dos 30 dias, os pesquisadores medirão a perda de peso total de cada sujeito.

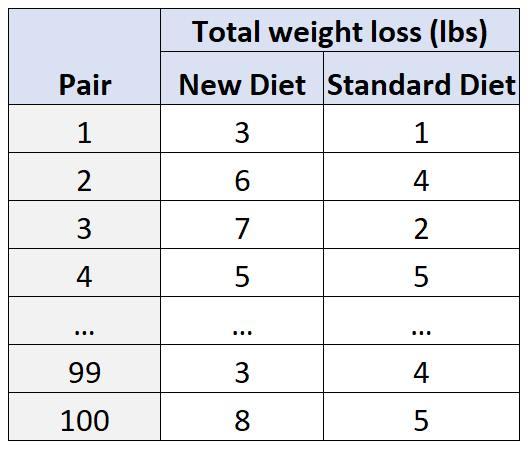
Ao utilizar este tipo de desenho, os investigadores podem ter a certeza de que quaisquer diferenças na perda de peso podem ser atribuídas ao tipo de dieta utilizada e não às variáveis confusas de idade e sexo .

Este tipo de design tem algumas desvantagens, incluindo:

1. Perder duas disciplinas se uma delas desistir. Se um sujeito decidir abandonar o estudo, você perderá dois sujeitos, pois não terá mais um par completo.

2. Leva tempo para encontrar correspondências . Encontrar tópicos que correspondam a determinadas variáveis, como sexo e idade, pode ser demorado.

3. Não é possível combinar os tópicos perfeitamente . Por mais que você tente, sempre haverá variações dentro dos assuntos de cada dupla.

Contudo, se um estudo tiver os recursos disponíveis para implementar este desenho, pode ser muito eficaz na eliminação dos efeitos de variáveis de confusão.