Биномиальное распределение

К бенджамин андерсон 3 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое биномиальное распределение в статистике и для чего оно используется. Таким образом, вы найдете определение биномиального распределения, примеры биномиальных распределений и свойства этого типа распределения вероятностей. Кроме того, вы сможете посчитать любую вероятность биномиального распределения с помощью онлайн-калькулятора.

Что такое биномиальное распределение?

Биномиальное распределение — это распределение вероятностей, которое подсчитывает количество успехов при выполнении серии независимых дихотомических экспериментов с постоянной вероятностью успеха.

Другими словами, биномиальное распределение — это распределение, которое описывает количество успешных результатов последовательности испытаний Бернулли.

Помните, что тест Бернулли — это эксперимент, имеющий два возможных результата: «успех» и «неуспех». Следовательно, если вероятность «успеха» равна p , вероятность «неудачи» равна q=1-p .

В общем, общее количество проведенных экспериментов определяется параметром n , а p — вероятность успеха каждого эксперимента. Таким образом, случайная величина, имеющая биномиальное распределение, записывается следующим образом:

$X\sim\text{Bin}(n,p)$

Обратите внимание, что при биномиальном распределении один и тот же эксперимент повторяется n раз, и эксперименты независимы друг от друга, поэтому вероятность успеха каждого эксперимента одинакова (p) .

Биномиальное распределение также можно назвать биномиальным распределением .

Примеры биномиального распределения

Увидев определение биномиального распределения, мы увидим несколько примеров переменных, которые соответствуют этому типу распределения, чтобы лучше понять эту концепцию.

Сколько раз выпадает решка при подбрасывании монеты 25 раз.
Количество бросков, сделанных баскетболистом при 60 бросках в корзину из одного и того же места.
Сколько раз мы получим число 6, бросив кубик 30 раз.
Число сдавших экзамен из 50 студентов.
Количество бракованных единиц в выборке из 100 изделий.

Формула биномиального распределения

Учитывая параметры x, n, p, функция вероятности биномиального распределения определяется как комбинаторное число n в x раз p ^x раз (1-p) ^nx .

Следовательно, формула расчета вероятности биномиального распределения имеет вид:

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать вероятность переменной, которая соответствует биномиальному распределению.

С другой стороны, кумулятивная вероятность биномиального распределения рассчитывается путем сложения вероятностей количества рассматриваемых случаев успеха и всех предыдущих вероятностей. Итак, формула расчета кумулятивной вероятности биномиального распределения:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Решенное упражнение на биномиальное распределение

Подбросив монету 10 раз, какова вероятность выпадения 6 орлов?

Переменная в этой задаче имеет биномиальное распределение, поскольку все запуски независимы друг от друга и имеют одинаковую вероятность успеха.

Конкретно вероятность успеха составляет 50%, поскольку успешным считается только один из двух возможных результатов.

$p=\cfrac{1}{2}=0,5$

Следовательно, распределение для этого упражнения представляет собой биномиальное число с общим числом 10 экспериментов и вероятностью 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Итак, чтобы определить вероятность выпадения шести орлов, нам нужно применить формулу биномиального распределения.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Итак, вероятность выпадения ровно шести орлов при десятикратном подбрасывании монеты равна 20,51%.

Характеристики биномиального распределения

Биномиальное распределение имеет следующие характеристики:

Биномиальное распределение определяется двумя параметрами: n — общее количество экспериментов Бернулли и, с другой стороны, p — вероятность успеха каждого эксперимента Бернулли.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

Среднее значение биномиального распределения равно произведению общего количества экспериментов, умноженному на вероятность успеха каждого эксперимента. Следовательно, чтобы вычислить среднее значение биномиального распределения, необходимо умножить n на p .

$E[X]=n\cdot p$

Дисперсия биномиального распределения равна общему количеству испытаний, умноженному на вероятность успеха и вероятность неудачи.

$Var(X)=n\cdot p\cdot (1-p)$

Формула функции вероятности биномиального распределения выглядит следующим образом:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Аналогично, формула для кумулятивной функции распределения биномиального распределения имеет вид:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Сумма двух независимых биномиальных распределений с одинаковой вероятностью эквивалентна биномиальному распределению с одинаковым значением вероятности p и n , представляющим собой сумму общего количества испытаний двух распределений.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

Распределение Бернулли представляет собой частный случай биномиального распределения, при котором n=1 , т.е. проводится только один эксперимент.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Если _X 1 , _X ₂ ,…, X _k — независимые случайные величины такие, что

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

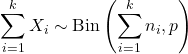
Калькулятор биномиального распределения

Введите значения параметров p, n и x биномиального распределения в следующий калькулятор, чтобы вычислить вероятность. Вам нужно выбрать вероятность, которую вы хотите рассчитать, и ввести числа, используя точку в качестве десятичного разделителя, например 0,1667.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше