Вероятность пересечения событий

В этой статье объясняется, как рассчитать вероятность пересечения событий. Так вы узнаете, какова формула вероятности пересечения событий, а также упражнения, решаемые пошагово.

Каково пересечение событий?

В теории вероятностей пересечение событий — это операция событий, результат которой складывается из элементарных событий, общих для всех событий операции. То есть пересечение событий А и Б образуется всеми событиями, принадлежащими А и Б одновременно.

Пересечение двух событий обозначается символом ⋂. Таким образом, пересечение событий A и B обозначается A⋂B.

Например, в случайном эксперименте с броском игральной кости, если одно событие заключается в том, что выпадает четное число A={2, 4, 6}, а другое событие заключается в том, что выпадает число больше трех B = {4, 5, 6 }, пересечение двух событий равно A⋂B={4, 6}.

Формула вероятности пересечения событий

Вероятность пересечения двух событий равна вероятности наступления одного события, умноженной на условную вероятность наступления другого события с учетом первого события.

Следовательно, формула вероятности пересечения двух событий имеет вид P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).

Золото:

• 

  И

  

  Это два зависимых события.

• 

  — вероятность пересечения события А и события Б.

• 

  вероятность того, что событие А произойдет.

• 

  — условная вероятность того, что событие B произойдет при данном событии A.

• 

  — вероятность того, что событие B произойдет.

• 

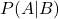
  — условная вероятность того, что событие A произойдет при данном событии B.

Однако если два события независимы, это означает, что вероятность возникновения одного события не зависит от того, произойдет ли другое событие. Следовательно, формула вероятности пересечения двух независимых событий выглядит следующим образом:

Золото:

• 

  И

  

  Это два независимых события.

• 

  — вероятность пересечения события A и события B.

• 

  это вероятность того, что событие А произойдет.

• 

  — вероятность того, что событие B произойдет.

Реальные примеры вероятности пересечения событий

Далее мы оставляем вам два примера, решенных шаг за шагом, чтобы вы могли увидеть, как рассчитывается вероятность пересечения двух событий. Сначала мы увидим пример пересечения двух независимых событий, а затем двух зависимых событий, чтобы вы могли увидеть оба случая.

Вероятность пересечения двух независимых событий

• Розыгрыш проводится три раза подряд. Найдите вероятность того, что при всех трех бросках выпадет решка.

В этом случае события, для которых мы хотим рассчитать совместную вероятность, независимы, поскольку результат розыгрыша не зависит от результата, полученного в предыдущем розыгрыше. Следовательно, чтобы определить вероятность выпадения трех последовательных орлов, мы должны использовать формулу вероятности пересечения независимых событий:

При жеребьевке возможны только два результата: мы можем получить орел или решку. Следовательно, вероятность выпадения орла или решки при подбрасывании монеты равна:

Итак, чтобы найти вероятность выпадения орла при всех трех подбрасываниях монеты, нам нужно умножить вероятность выпадения орла на три:

Короче говоря, вероятность выпадения орла три раза подряд составляет 12,5%.

Вероятность пересечения двух зависимых событий

• В пустую коробку положим 8 синих шаров, 4 оранжевых шара и 2 зеленых шара. Если мы сначала вытянем один шар, а затем другой, не кладя первый вытянутый шар обратно в коробку, какова вероятность того, что первый шар будет синим, а второй — оранжевым?

В данном случае события зависимы, поскольку вероятность подобрать оранжевый шар во втором розыгрыше зависит от цвета шара, выпавшего в первом розыгрыше. Поэтому для расчета вероятности, которую нам задает задача, необходимо воспользоваться формулой вероятности пересечения зависимых событий:

Вероятность получения синего шара в первом розыгрыше легко определить, просто разделив количество синих шаров на общее количество шаров:

С другой стороны, вероятность вытянуть оранжевый шар после взятия синего шара рассчитывается иначе, поскольку количество оранжевых шаров другое и, кроме того, внутри коробки теперь на один шар меньше:

Таким образом, вероятность выпадения сначала синего шара, а затем оранжевого шара рассчитывается путем умножения двух найденных выше вероятностей:

Свойства пересечения событий

В теории вероятностей пересечение событий обладает следующими свойствами:

• Коммутативное свойство: порядок событий пересечения не меняет результат операции.

• Ассоциативное свойство: пересечение трех событий можно вычислять в любом порядке, поскольку результат один и тот же.

• Распределительное свойство: пересечение событий удовлетворяет распределительному свойству при объединении событий.