Как найти вероятность выпадения хотя бы одного орла при броске монеты
Для данного подбрасывания монеты вероятность выпадения орла составляет 1/2 или 0,5.
Чтобы найти вероятность выпадения хотя бы одного орла при определенном количестве подбрасываний монеты, можно использовать следующую формулу:
P(хотя бы одна головка) = 1 – 0,5 n
Золото:
- n : Общее количество разворотов
Например, предположим, что мы подбрасываем монету 2 раза.
Вероятность выпадения хотя бы одной головы за эти 3 броска равна:
- P(хотя бы одна головка) = 1 – 0,5 n
- P(хотя бы одна головка) = 1 – 0,5 3
- P (хотя бы одна голова) = 1 – 0,125
- P(хотя бы одна голова) = 0,875
Этот ответ имеет смысл, если мы перечислим все возможные результаты для двух подбрасываний монеты, где «T» обозначает орел, а «H» — решку:
- ТТТ
- ТТХ
- ТХХ
- ТТТ
- ХХХХ
- ВРД
- ХТХ
- ХТТ
Обратите внимание, что хотя бы одна голова (H) появляется в 7 из 8 возможных исходов, что соответствует 7/8 = 0,875 .
Или предположим, что мы подбрасываем монету 5 раз.
Вероятность выпадения хотя бы одной головы за эти 5 бросков равна:
- P(хотя бы одна головка) = 1 – 0,5 n
- P(хотя бы одна голова) = 1 – 0,5 5
- P(хотя бы одна голова) = 1 – 0,25
- P(хотя бы одна голова) = 0,96875
В следующей таблице показана вероятность выпадения хотя бы одного орла при разном количестве подбрасываний монеты:
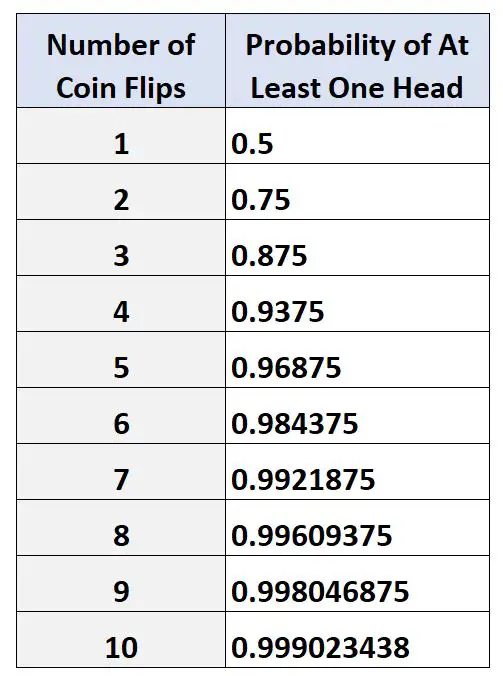
Обратите внимание: чем больше количество подбрасываний монеты, тем выше вероятность выпадения хотя бы одного орла.
Это должно иметь смысл, учитывая, что у нас должна быть более высокая вероятность появления орла, если мы продолжим подбрасывать монету несколько раз.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные вычисления, связанные с вероятностью:
Как найти вероятность «хотя бы одного» успеха
Как найти вероятность «хотя бы двух» успехов
Как найти вероятность событий A и B
Как найти вероятность A или B