Что такое сбивающая с толку переменная? (определение & #038; пример)

В любом эксперименте есть две основные переменные:

Независимая переменная: переменная, которую экспериментатор изменяет или контролирует, чтобы иметь возможность наблюдать влияние на зависимую переменную.

Зависимая переменная: переменная, измеренная в эксперименте, которая «зависит» от независимой переменной.

Исследователей часто интересует понимание того, как изменения независимой переменной влияют на зависимую переменную.

Однако иногда случается, что третья переменная не принимается во внимание и это может повлиять на взаимосвязь между двумя изучаемыми переменными.

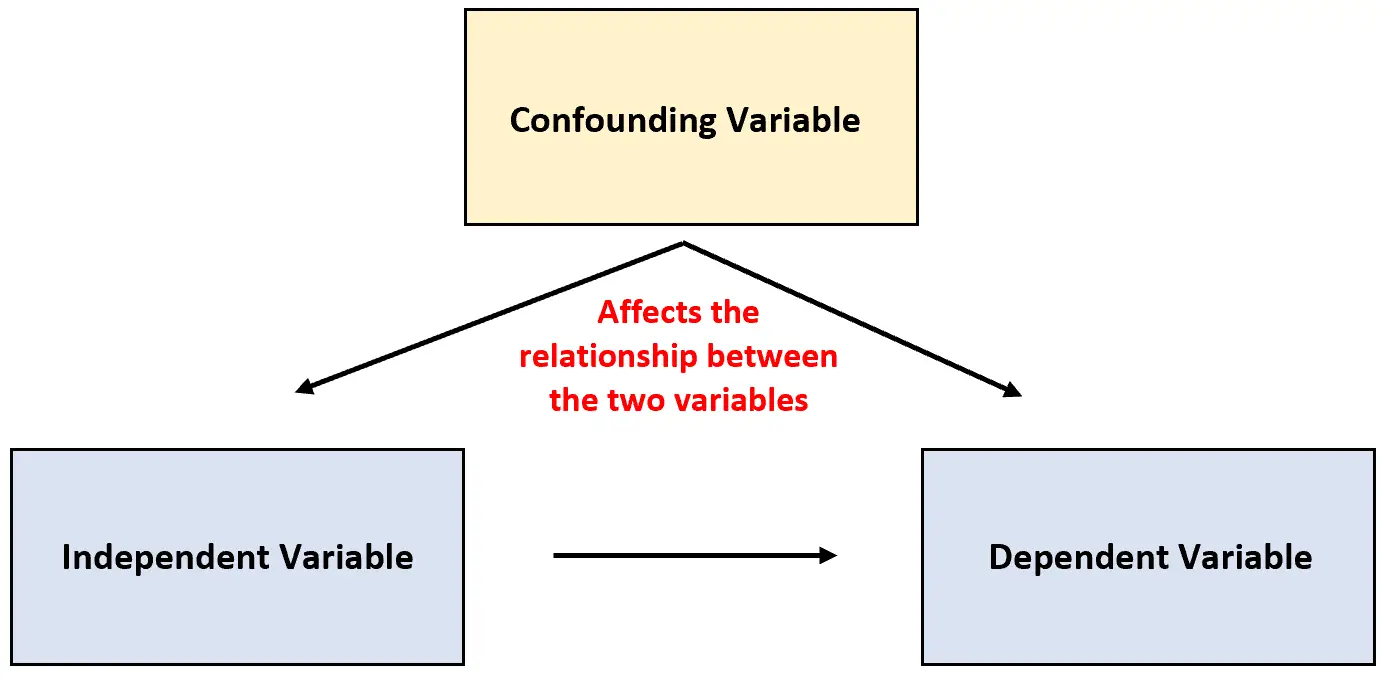
Этот тип переменной известен как мешающая переменная , и он может сбить с толку результаты исследования и создать впечатление, будто между двумя переменными существует какой-то тип причинно-следственной связи, которого на самом деле не существует.

Смешивающая переменная: переменная, которая не включена в эксперимент, но влияет на взаимосвязь между двумя переменными в эксперименте.

Этот тип переменных может исказить результаты эксперимента и привести к ненадежным результатам.

Например, предположим, что исследователь собирает данные о продажах мороженого и нападениях акул и обнаруживает, что эти две переменные тесно связаны. Означает ли это, что увеличение продаж мороженого приводит к увеличению количества нападений акул?

Это маловероятно. Наиболее вероятная причина — сбивающая с толку переменная температура . Когда на улице теплее, больше людей покупают мороженое и больше людей отправляются на океан.

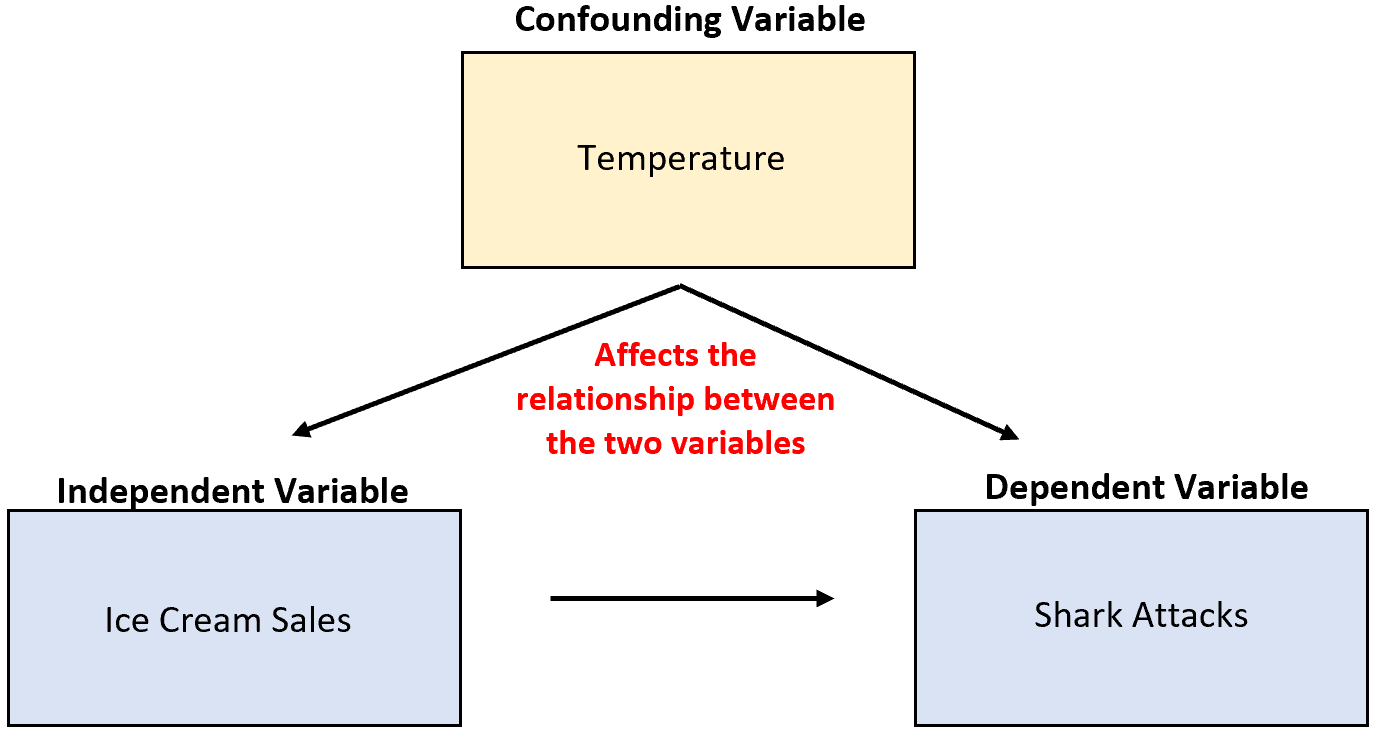
Требования к запутанным переменным

Чтобы переменная была запутанной, она должна отвечать следующим требованиям:

1. Она должна быть коррелирована с независимой переменной.

В предыдущем примере температура коррелировала с независимой переменной продаж мороженого. В частности, более высокие температуры связаны с более высокими продажами мороженого, а более низкие температуры – с более низкими продажами.

2. Должна существовать причинно-следственная связь с зависимой переменной.

В предыдущем примере температура оказала прямое причинное влияние на количество нападений акул. В частности, более высокие температуры загоняют больше людей в океан, что напрямую увеличивает вероятность нападения акул.

Почему путаница переменных проблематична?

Смешивающие переменные проблематичны по двум причинам:

1. Смешивающие переменные могут создать впечатление, что причинно-следственные связи существуют, хотя на самом деле это не так.

В нашем предыдущем примере из-за запутанной переменной температуры создалось впечатление, что между продажей мороженого и нападениями акул существует причинно-следственная связь.

Однако мы знаем, что продажа мороженого не вызывает нападения акул. Из-за запутанной переменной температуры это кажется именно таким.

2. Смешение переменных может скрыть истинную причинно-следственную связь между переменными.

Предположим, мы изучаем способность физических упражнений снижать кровяное давление. Потенциальной мешающей переменной является начальный вес, который коррелирует с физической нагрузкой и оказывает прямое причинное влияние на кровяное давление.

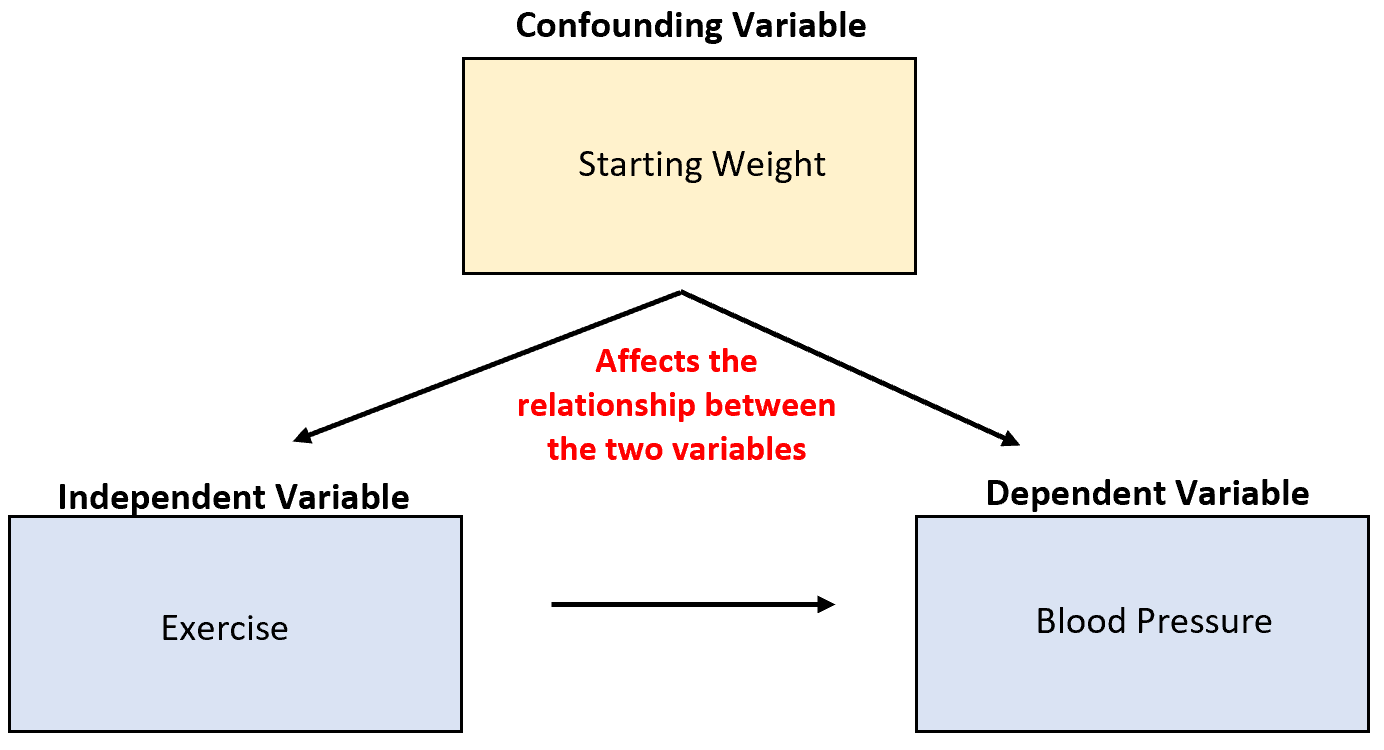
Хотя повышенная физическая активность может привести к снижению артериального давления, стартовый вес человека также оказывает большое влияние на взаимосвязь между этими двумя переменными.

Смешивающие переменные и внутренняя валидность

С технической точки зрения, смешивающие переменные влияют на внутреннюю достоверность исследования, которая относится к достоверности приписывания любых изменений зависимой переменной изменениям независимой переменной.

Когда присутствуют вмешивающиеся переменные, мы не всегда можем с уверенностью сказать, что изменения, которые мы наблюдаем в зависимой переменной, являются прямым результатом изменений независимой переменной.

Как уменьшить эффект путаницы переменных

Существует несколько способов уменьшить эффект путаницы переменных, включая следующие методы:

1. Случайное распределение

Случайное распределение относится к процессу случайного распределения участников исследования в группу лечения или контрольную группу.

Например, предположим, что мы хотим изучить влияние новой таблетки на кровяное давление. Если мы наберем 100 человек для участия в исследовании, мы могли бы использовать генератор случайных чисел, чтобы случайным образом распределить 50 человек в контрольную группу (без таблеток) и 50 человек в группу лечения (новые таблетки).

Используя случайное распределение, мы увеличиваем вероятность того, что обе группы будут иметь примерно схожие характеристики, а это означает, что любые различия, наблюдаемые между двумя группами, можно отнести на счет лечения.

Это означает, что исследование должно иметь внутреннюю валидность : любые различия в кровяном давлении между группами можно связать с самой таблеткой, а не с различиями между людьми в группах.

2. Блокировка

Блокирование относится к практике разделения участников исследования на «блоки» на основе определенного значения искажающей переменной, чтобы устранить влияние искажающей переменной.

Например, предположим, что исследователи хотят понять влияние новой диеты на потерю веса. Независимая переменная — это новая диета, а зависимая переменная — величина потери веса.

Однако есть одна мешающая переменная, которая может вызвать изменения в потере веса, — это пол . Вполне вероятно, что пол человека повлияет на то, сколько веса он потеряет, независимо от того, работает новая диета или нет.

Один из способов решения этой проблемы — поместить индивидуумов в один из двух блоков:

• Мужской
• Женский

Затем в каждом блоке мы случайным образом распределяли людей по одному из двух методов лечения:

• Новая диета
• Стандартная диета

Сделав это, различия внутри каждого блока будут намного ниже, чем различия между всеми людьми, и мы сможем лучше понять, как новая диета влияет на потерю веса, контролируя при этом пол.

3. Переписка

План согласованных пар — это тип экспериментального плана, в котором мы «сопоставляем» людей на основе значений потенциальных искажающих переменных.

Например, предположим, что исследователи хотят знать, как новая диета влияет на потерю веса по сравнению со стандартной диетой. Двумя потенциально запутанными переменными в этой ситуации являются возраст и пол .

Чтобы учесть это, наберите исследователей 100 человек, а затем сгруппируйте их в 50 пар в зависимости от возраста и пола. Например:

• 25-летнему мужчине будет подобран другой 25-летний мужчина, так как они «совпадают» по возрасту и полу.
• 30-летней женщине будет подобрана другая 30-летняя женщина, поскольку они также совпадают по возрасту, полу и т. д.

Затем в каждой паре одному субъекту случайным образом будет назначено соблюдать новую диету в течение 30 дней, а другому субъекту будет назначено соблюдать стандартную диету в течение 30 дней.

По истечении 30 дней исследователи измерят общую потерю веса для каждого испытуемого.

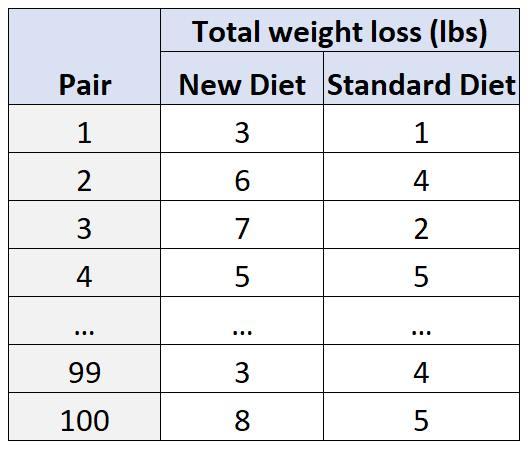
Используя этот тип дизайна, исследователи могут быть уверены, что любые различия в потере веса могут быть связаны с типом используемой диеты, а не с мешающими переменными возраста и пола .

Этот тип конструкции имеет ряд недостатков, среди которых:

1. Потерять два предмета, если один из них выпадет. Если испытуемый решает выйти из исследования, вы фактически теряете двух испытуемых, поскольку у вас больше нет полной пары.

2. Чтобы найти совпадения, нужно время . Поиск тем, соответствующих определенным переменным, таким как пол и возраст, может занять много времени.

3. Не могу идеально согласовать темы . Как бы вы ни старались, в предметах каждой пары всегда будут различия.

Однако, если у исследования есть ресурсы для реализации этого плана, оно может быть очень эффективным в устранении влияния мешающих переменных.