Выборочное среднее значение

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье вы узнаете, что такое выборочное среднее в статистике. Кроме того, вы найдете, как рассчитать среднее значение выборки, решение упражнения и, кроме того, онлайн-калькулятор для расчета среднего значения любой выборки.

Что означает выборка?

В статистике выборочное среднее — это среднее значение выборки. Чтобы вычислить выборочное среднее, все значения в выборке необходимо сложить, а затем разделить на общее количество данных в выборке.

Символ образца означает

$\overline{x}$

В статистическом исследовании, как правило, не все значения совокупности известны, поэтому отбирается выборка совокупности для ее анализа и экстраполяции полученных выводов на всю совокупность. Таким образом, выборочное среднее значение используется для оценки среднего значения генеральной совокупности.

Пример формулы среднего значения

Среднее значение выборки равно сумме всех значений выборки, деленной на размер выборки. То есть для расчета выборочного среднего все значения в выборке складываются, а затем делятся на общее количество данных в выборке.

Таким образом, формула для расчета выборочного среднего выглядит так:

$\displaystyle\overline{x}=\frac{\displaystyle \sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}$

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать выборочное среднее любого набора данных.

Имейте в виду, что выборочное среднее рассчитывается с использованием данных выборки, поэтому значение генерального среднего может отличаться от расчетного значения.

Пример расчета среднего значения

Теперь, когда мы знаем определение выборочного среднего значения и его формулу, давайте посмотрим, как получить выборочное среднее значение из набора данных, решив простой пример.

Хосе хочет переехать в центр города, но у него мало времени, поэтому он не может проанализировать цены на все квартиры, сдаваемые в аренду. Итак, вы решаете посмотреть только на стоимость аренды пяти квартир (показана ниже), чтобы узнать, во сколько вам обойдется жизнь в центре города. Какова средняя цена образца?

600 евро 430 евро 820 евро 575 евро 950 евро

Чтобы найти выборочное среднее, нам нужно сложить все выборочные значения, а затем разделить на общее количество наблюдений, равное 5. Итак, мы применяем формулу выборочного среднего:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+x_3+x_4+x_5}{n}$

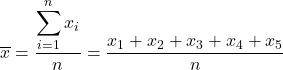
Далее подставляем данные в формулу и вычисляем выборочное среднее:

$\overline{x}=\cfrac{600+430+820+575+950}{5}=675$

Если кратко, то средняя цена отобранных для выборки квартир составляет 675 евро.

Пример расчета среднего значения

Введите данные из любой статистической выборки в следующий калькулятор, чтобы рассчитать ее выборочное среднее значение. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Среднее выборочное и среднее генеральное

Среднее значение населения — это среднее значение статистической совокупности . Таким образом, средний показатель по численности населения представляет собой среднее значение всех элементов, по которым планируется провести статистическое исследование.

Следовательно, разница между средним значением выборки и средним значением генеральной совокупности заключается в том, что среднее выборочное является средним значением выборки, а среднее генеральной совокупности — средним значением значений генеральной совокупности.

Чтобы отличить выборочное среднее от генерального среднего, они представлены разными символами. Символ образца означает

$\overline{x}$

, а символ численности населения означает

$\mu$

$\begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}$

Выборочное среднее используется для оценки значения генерального среднего значения, что можно сделать с помощью точечной или интервальной оценки .

➤ См.: Какова средняя численность населения?

Выборочное распределение выборочных средних

Наконец, давайте посмотрим, что означает выборочное распределение выборки, поскольку это статистическая концепция, которая может сбить с толку.

Во-первых, давайте начнем с определения того, что такое выборочное распределение. Выборочное распределение — это распределение, которое получается в результате учета всех возможных выборок из статистической совокупности.

Следовательно, выборочное распределение выборочного среднего — это распределение, которое получается в результате вычисления среднего значения каждой возможной выборки из совокупности. То есть, если мы изучаем все возможные выборки из совокупности и вычисляем среднее значение каждой из выборок, набор рассчитанных значений представляет собой выборочное распределение выборочного среднего.

В заключение, хотя выборочное среднее и выборочное распределение имеют схожие названия, необходимо знать, как их различать: выборочное среднее — это статистический параметр, который рассчитывается на основе выборки, с другой стороны, выборочное распределение — это распределение. это результат изучения всех выборок, которые можно получить из популяции.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что означает выборка?

Пример формулы среднего значения

Пример расчета среднего значения

Пример расчета среднего значения

Среднее выборочное и среднее генеральное

Выборочное распределение выборочных средних

Об авторе

бенджамин андерсон

Добавить комментарий