Однофакторный дисперсионный анализ: определение, формула и пример
Односторонний дисперсионный анализ («дисперсионный анализ») сравнивает средние значения трех или более независимых групп, чтобы определить, существует ли статистически значимая разница между средними значениями соответствующей совокупности.
В этом руководстве объясняется следующее:
- Мотивация выполнить однофакторный дисперсионный анализ.
- Допущения, которые должны быть выполнены для выполнения одностороннего дисперсионного анализа.
- Процесс выполнения одностороннего дисперсионного анализа.
- Пример того, как выполнить однофакторный дисперсионный анализ.
Односторонний дисперсионный анализ: мотивация
Предположим, мы хотим знать, приводят ли три разные программы подготовки к экзаменам к разным средним баллам на вступительном экзамене в колледж. Поскольку по всей стране миллионы старшеклассников, было бы слишком много времени и денег, чтобы объехать каждого ученика и позволить ему воспользоваться одной из программ подготовки к экзаменам.
Вместо этого мы могли бы выбрать три случайные выборки из 100 студентов из совокупности и позволить каждой выборке использовать одну из трех программ подготовки к экзамену. Тогда мы могли бы записывать баллы каждого студента после сдачи экзамена.
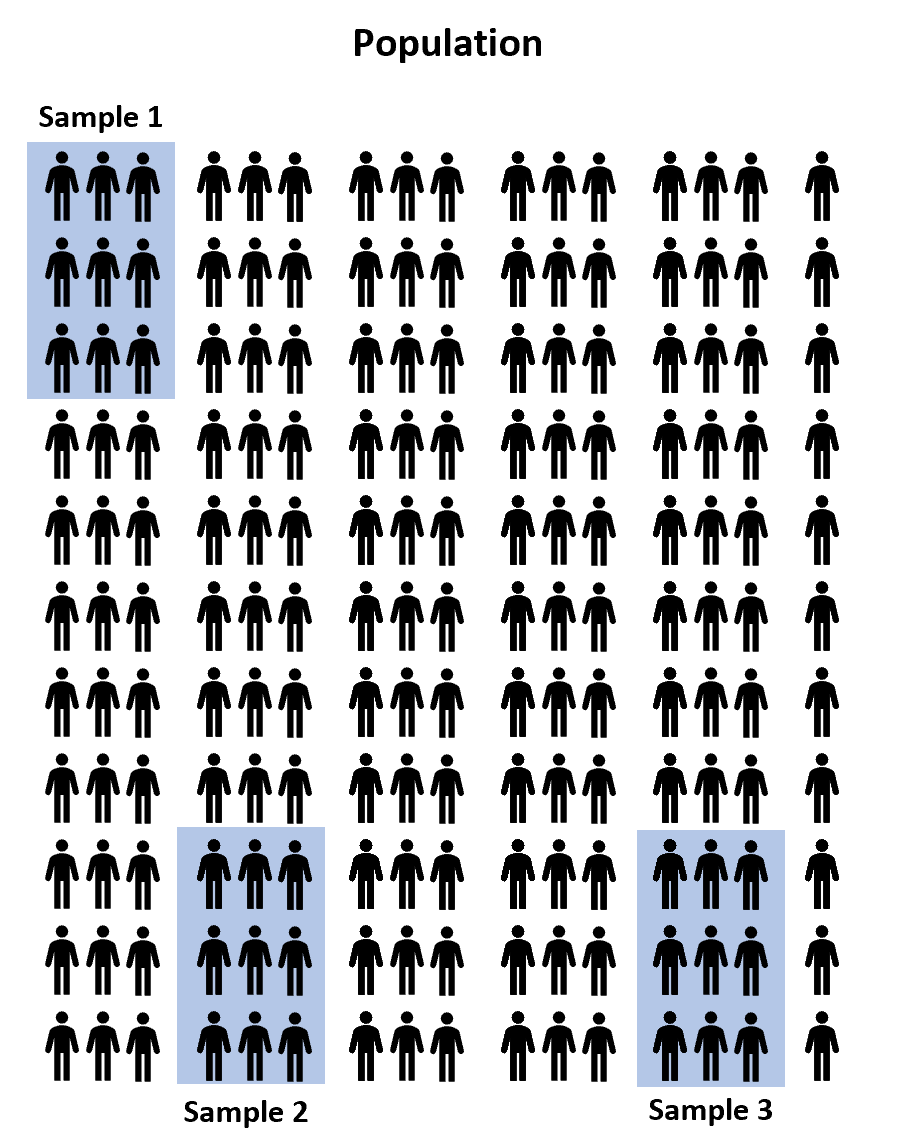
Однако практически гарантировано, что средний балл экзамена между тремя выборками будет хотя бы немного отличаться. Вопрос в том, является ли эта разница статистически значимой . К счастью, односторонний дисперсионный анализ позволяет нам ответить на этот вопрос.
Односторонний дисперсионный анализ: предположения
Чтобы результаты однофакторного дисперсионного анализа были действительными, должны выполняться следующие допущения:
1. Нормальность . Каждая выборка была взята из нормально распределенной популяции.
2. Равные дисперсии . Дисперсии совокупностей, из которых взяты выборки, равны. Чтобы проверить эту гипотезу, вы можете использовать тест Бартлетта .
3. Независимость . Наблюдения внутри каждой группы независимы друг от друга, а наблюдения внутри групп были получены методом случайной выборки.
Прочтите эту статью , чтобы узнать подробнее о том, как проверить эти предположения.
Односторонний дисперсионный анализ: процесс
Односторонний дисперсионный анализ использует следующие нулевые и альтернативные гипотезы:
- H 0 (нулевая гипотеза): μ 1 = μ 2 = μ 3 = … = μ k (все средние значения совокупности равны)
- H 1 (альтернативная гипотеза): по крайней мере одно среднее значение популяции отличается отдых
Обычно вы используете какое-либо статистическое программное обеспечение (например, R, Excel, Stata, SPSS и т. д.) для выполнения однофакторного дисперсионного анализа, поскольку выполнять его вручную утомительно.
Независимо от используемого вами программного обеспечения, вы получите следующую таблицу:
| Источник | Сумма квадратов (СС) | дф | Среднеквадратичные (МС) | Ф | п |
|---|---|---|---|---|---|
| Уход | RSS | дф р | МСР | МСР/МСЭ | F df r , df e |
| Ошибка | ЭСС | df е | МШЭ | ||
| Общий | ОХС | дф т |
Золото:
- SSR: регрессия суммы квадратов
- SSE: сумма квадратов ошибок
- SST: общая сумма квадратов (SST = SSR + SSE)
- df r : степени свободы регрессии (df r = k-1)
- df e : степени свободы ошибки (df e = nk)
- df t : общее количество степеней свободы (df t = n-1)
- k: общее количество групп
- n: общее количество наблюдений
- MSR: среднеквадратическая регрессия (MSR = SSR/df r )
- MSE: среднеквадратическая ошибка (MSE = SSE/df e )
- F: Статистика F-теста (F = MSR/MSE).
- p: значение p, соответствующее F dfr, dfe.
Если значение p меньше выбранного уровня значимости (например, 0,05), то вы можете отклонить нулевую гипотезу и сделать вывод, что по крайней мере одно из средних значений генеральной совокупности отличается от других.
Примечание. Если вы отвергаете нулевую гипотезу, это означает, что по крайней мере одно из средних значений генеральной совокупности отличается от других, но в таблице ANOVA не указано, какие средние значения генеральной совокупности отличаются. Чтобы определить это, вам необходимо выполнить апостериорное тестирование , также называемое тестированием «множественного сравнения».
Односторонний дисперсионный анализ: пример
Предположим, мы хотим знать, приводят ли три разные программы подготовки к экзамену к разным средним баллам на данном экзамене. Чтобы проверить это, мы набираем 30 студентов для участия в исследовании и делим их на три группы.
Студентам в каждой группе случайным образом назначаются использовать одну из трех программ подготовки к экзамену в течение следующих трех недель для подготовки к экзамену. В конце трех недель все студенты сдают один и тот же экзамен.
Результаты экзамена для каждой группы показаны ниже:

Чтобы выполнить однофакторный дисперсионный анализ для этих данных, мы будем использовать статистический калькулятор однофакторного дисперсионного анализа со следующими входными данными:

Из выходной таблицы мы видим, что статистика F-теста равна 2,358 , а соответствующее значение p — 0,11385 .

Поскольку это значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что существует статистически значимая разница между средними баллами экзаменов трех групп.
Дополнительные ресурсы
В следующих статьях объясняется, как выполнить однофакторный дисперсионный анализ с использованием различного статистического программного обеспечения:
Как выполнить однофакторный дисперсионный анализ в Excel
Как выполнить односторонний дисперсионный анализ в R
Как выполнить однофакторный дисперсионный анализ в Python
Как выполнить односторонний дисперсионный анализ в SAS
Как выполнить однофакторный дисперсионный анализ в SPSS
Как выполнить однофакторный дисперсионный анализ в Stata
Как выполнить однофакторный дисперсионный анализ на калькуляторе TI-84
Онлайн-калькулятор однофакторного дисперсионного анализа