Гетероскедастичность

В этой статье объясняется, что такое гетероскедастичность в статистике. Дополнительно вы узнаете, что вызывает гетероскедастичность, каковы ее последствия и как ее исправить.

Что такое гетероскедастичность?

В статистике гетероскедастичность — это характеристика, которая представляет собой модель регрессии, подразумевающую, что дисперсия ошибок не является постоянной. Другими словами, гетероскедастическая модель означает, что ее ошибки имеют нерегулярную дисперсию, тогда модель называется гетероскедастической.

Помните, что ошибка (или остаток) определяется как разница между реальным значением и значением, оцененным с помощью регрессионной модели.

При построении регрессионной модели ошибка каждого наблюдения рассчитывается с использованием предыдущего выражения. Таким образом, статистическая модель является гетероскедастической, когда дисперсия рассчитанных ошибок не является постоянной на протяжении наблюдений, а, скорее, меняется.

Хотя это может показаться очень простым, важно, чтобы модель регрессии не представляла гетероскедастичности, поскольку расчет модели основан на том факте, что дисперсия остатков постоянна, фактически это одно из предыдущих предположений регрессионные модели.

Существуют определенные статистические тесты, которые могут обнаружить гетероскедастичность, например тест Уайта или тест Гольдфельда-Квандта. Однако обычно путем построения графика остатков можно определить их гетероскедастичность.

Причины гетероскедастичности

Наиболее распространенными причинами гетероскедастичности в модели являются:

• Когда диапазон данных очень широк по сравнению со средним. Если в одной и той же статистической выборке присутствуют очень большие значения и очень маленькие значения, вполне вероятно, что полученная регрессионная модель является гетероскедастической.
• Исключение переменных в регрессионной модели также приводит к гетероскедастичности. Логично, что если соответствующая переменная не включена в модель, ее изменение будет включено в остатки, и это не обязательно будет зафиксировано.
• Аналогичным образом, изменение структуры может привести к плохому согласованию модели с набором данных, и, следовательно, дисперсия остатков может не быть постоянной.
• Когда некоторые переменные имеют гораздо большие значения, чем другие объясняющие переменные, модель может иметь гетероскедастичность. В этом случае переменные могут быть релятивизированы для решения проблемы.

Однако в некоторых случаях по своей природе может проявляться гетероскедастичность. Например, если мы смоделируем доход человека с его расходами на еду, у более богатых людей будет гораздо большая вариативность в своих расходах на еду, чем у более бедных людей. Потому что богатый человек иногда ест в дорогих ресторанах, а иногда в дешевых, в отличие от бедного человека, который всегда ест в дешевых ресторанах. Следовательно, регрессионная модель легко может обладать гетероскедастичностью.

Последствия гетероскедастичности

В основном последствия гетероскедастичности в регрессионной модели заключаются в следующем:

• Эффективность теряется в методе наименьших квадратов, определяемом как среднее значение квадратов ошибок.
• Ошибки возникают при вычислении ковариационной матрицы методов наименьших квадратов.

Правильная гетероскедастичность

Если полученная модель регрессии гетероскедастична, мы можем попробовать следующие поправки для получения гетероскедастичности:

• Вычислите натуральный логарифм независимой переменной. Обычно это полезно, когда на графике увеличивается дисперсия остатков.
• В зависимости от остаточного графика более практичным может оказаться другой тип преобразования независимой переменной. Например, если график имеет форму параболы, мы можем вычислить квадрат независимой переменной и добавить эту переменную в модель.
• В модели также можно использовать другие переменные; удалив или добавив переменную, можно изменить дисперсию остатков.
• Вместо использования критерия наименьших квадратов можно использовать взвешенный критерий наименьших квадратов.

Гетероскедастичность и гомоскедастичность

Наконец, мы увидим, каковы различия между гетероскедастичностью и гомоскедастичностью в статистике, поскольку это две концепции регрессионных моделей, о которых мы должны четко понимать.

Гомоскедастичность регрессионной модели — это статистическая характеристика, указывающая на постоянство дисперсии ошибок. Таким образом, гомоскедастическая модель означает, что дисперсия ее ошибок постоянна.

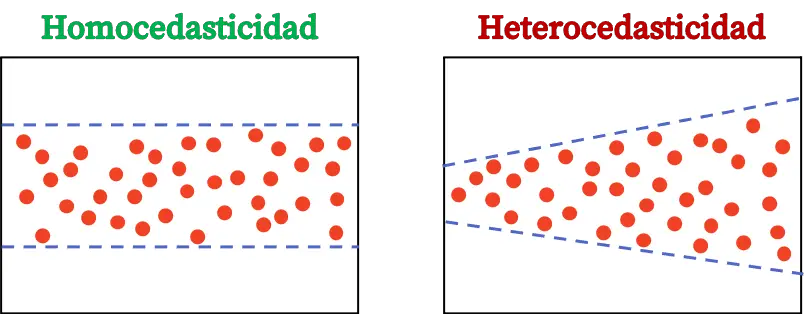
Разница между гетероскедастичностью и гомоскедастичностью заключается в постоянстве дисперсии остатков. Если дисперсия остатков модели не постоянна, это означает, что модель гетероскедастична. С другой стороны, если дисперсия остатков постоянна, это означает, что она гомоскедастична.

Следовательно, нам необходимо убедиться, что построенная нами регрессионная модель является гомоскедастической, таким образом будет выполнено предположение о том, что дисперсия остатков постоянна.