Как создать остаточный график в python
График остатков — это тип графика, который отображает подобранные значения в сравнении с остатками регрессионной модели .
Этот тип графика часто используется для оценки того, подходит ли модель линейной регрессии для данного набора данных, а также для проверки остатков на гетероскедастичность .
В этом руководстве объясняется, как создать остаточный график для модели линейной регрессии в Python.
Пример: остаточный график в Python
В этом примере мы будем использовать набор данных, описывающий характеристики 10 баскетболистов:
import numpy as np import pandas as pd #create dataset df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86], 'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19], 'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5], 'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]}) #view dataset df rating points assists rebounds 0 90 25 5 11 1 85 20 7 8 2 82 14 7 10 3 88 16 8 6 4 94 27 5 6 5 90 20 7 9 6 76 12 6 6 7 75 15 9 10 8 87 14 9 10 9 86 19 5 7
Остаточный график для простой линейной регрессии
Предположим, мы подбираем простую модель линейной регрессии, используя баллы в качестве предикторной переменной и оценку в качестве переменной отклика:
#import necessary libraries import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.formula.api import ols #fit simple linear regression model model = ols('rating ~ points', data=df). fit () #view model summary print(model.summary())
Мы можем создать остаточный или подобранный график, используя функциюplot_regress_exog() из библиотеки statsmodels:
#define figure size fig = plt.figure(figsize=(12,8)) #produce regression plots fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)
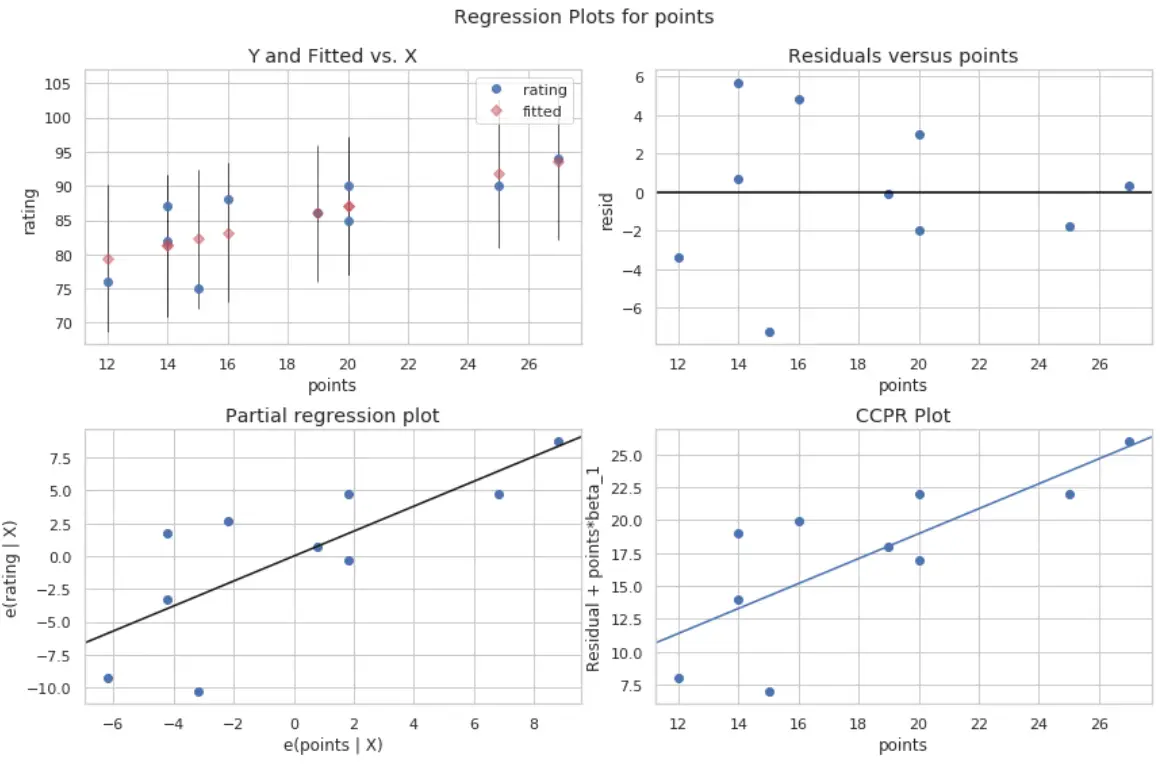
Создаются четыре сюжета. В правом верхнем углу показан остаточный график по сравнению с скорректированным графиком. Ось X на этом графике показывает фактические значения точек переменной-предиктора, а ось Y показывает невязку для этого значения.
Поскольку остатки кажутся случайным образом разбросанными вокруг нуля, это указывает на то, что гетероскедастичность не является проблемой для переменной-предиктора.
Остаточные графики для множественной линейной регрессии
Предположим, что вместо этого мы подбираем модель множественной линейной регрессии, используя передачи и подборы в качестве предикторной переменной, а рейтинг в качестве переменной ответа:
#fit multiple linear regression model model = ols('rating ~ assists + rebounds', data=df). fit () #view model summary print(model.summary())
Еще раз, мы можем создать график остатков и предикторов для каждого из отдельных предикторов, используя функциюplot_regress_exog() из библиотеки statsmodels.
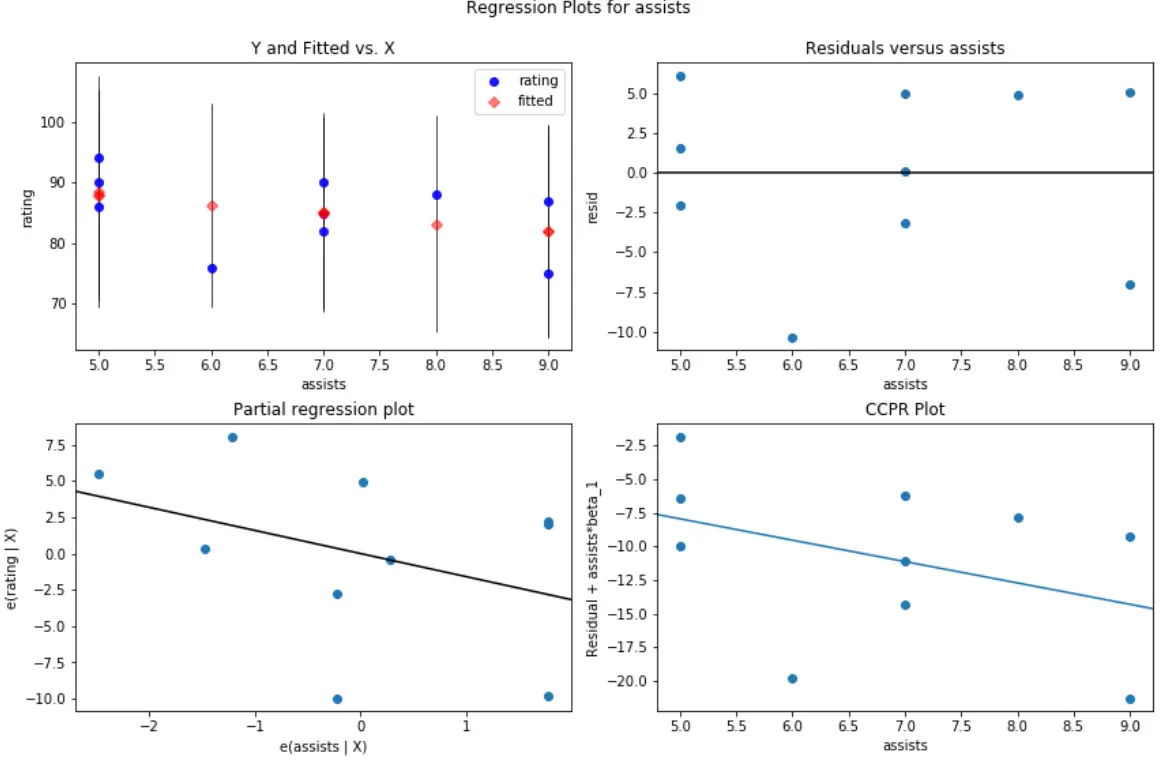
Например, вот как выглядит график остатка/предиктора для вспомогательных переменных -предикторов :
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)
А вот как выглядит график остатка/предиктора для переменной-предиктора отскока :
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)
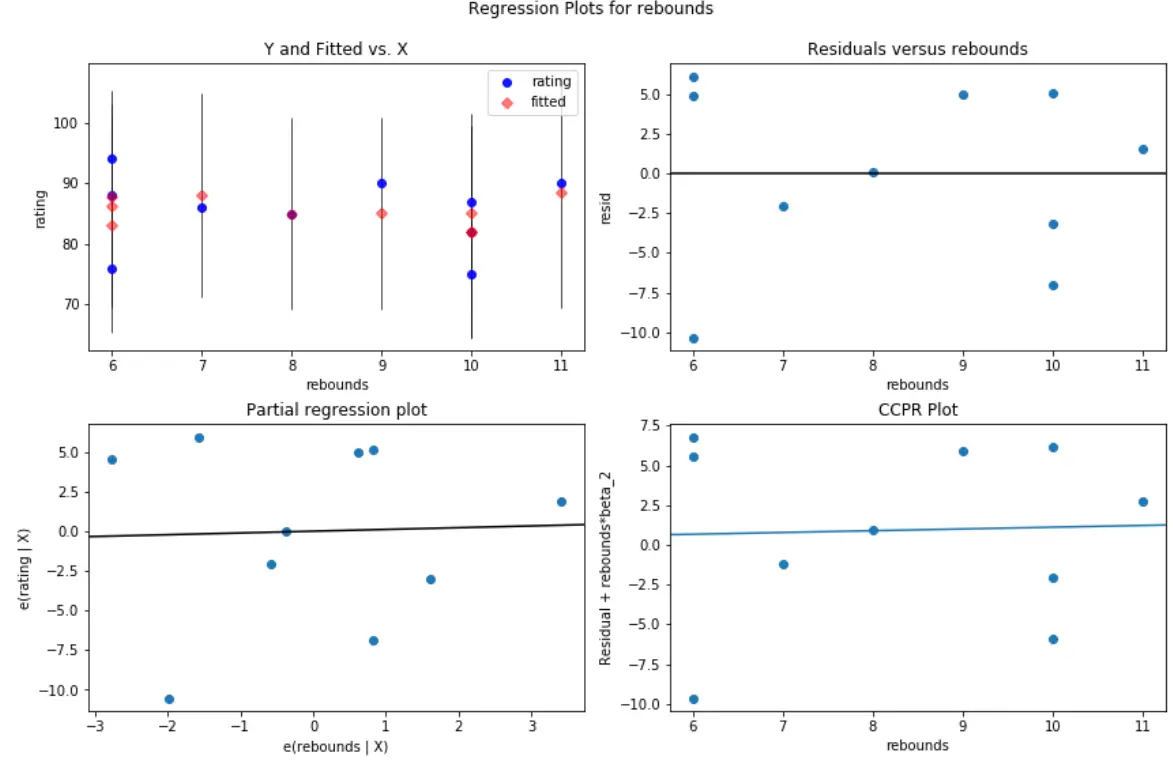
На обоих графиках остатки случайным образом разбросаны вокруг нуля, что указывает на то, что гетероскедастичность не является проблемой ни для одной из переменных-предикторов в модели.