Доверительный интервал для доли
В этой статье объясняется, что такое доверительный интервал для пропорции и для чего он используется в статистике. Кроме того, вы узнаете, как рассчитать доверительный интервал пропорции, а также решите упражнение, чтобы лучше понять эту концепцию.
Каков доверительный интервал пропорции?
Доверительный интервал доли — это интервал, который обеспечивает диапазон допустимых значений доли популяции. То есть доверительный интервал для доли указывает максимальное значение и минимальное значение, между которыми доля населения находится с погрешностью.
Например, если доверительный интервал для доли населения с уровнем достоверности 95% равен (0,73, 0,81), это означает, что доля населения находится между 73% и 81% с вероятностью 95%.
Поэтому доверительный интервал доли используется для оценки значения доли популяции, соответствующей определенным характеристикам.
Как мы увидим в следующем разделе, доверительный интервал для доли зависит от доли выборки и количества наблюдений в выборке.
Формула доверительного интервала для доли
Доверительный интервал для доли рассчитывается путем сложения и вычитания из выборочной доли значения Z α/2 , умноженного на квадратный корень из выборочной доли (p), умноженного на 1-p и разделенного на размер выборки (n). Следовательно, формула расчета доверительного интервала для доли имеет вид:

Золото:
-

– это доля выборки.
-

это размер выборки.
-

— квантиль стандартного нормального распределения, соответствующий вероятности α/2. Для больших размеров выборки и уровня достоверности 95% оно обычно близко к 1,96, а для уровня достоверности 99% оно обычно близко к 2,576.
Пример расчета доверительного интервала для доли
Чтобы вы могли увидеть, как рассчитывается доверительный интервал для пропорции, мы оставляем вам пошаговый конкретный пример.
- Страховая компания хочет провести исследование рынка и определить, сколько людей в стране имеют страхование жизни. Для этого анализируется случайная выборка из 700 человек и приходим к выводу, что 40% выборки имеют страхование жизни. Каков доверительный интервал при доверительном уровне 95% для доли населения страны?
Чтобы определить доверительный интервал доли населения, нам нужно использовать формулу, которую мы видели выше:

В этом случае мы хотим, чтобы уровень достоверности доверительного интервала составлял 95%, поэтому значение Z α/2 , которое нам нужно принять, равно 1,96.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
В постановке задачи уже сказано, что размер выборки равен n=700 и наблюдаемая доля в выборке равна p=0,40, поэтому подставляем данные в формулу доверительного интервала для доли и вычисляем пределы интервала:

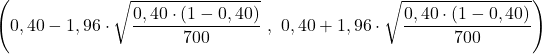
![]()
В заключение следует отметить, что доля изученной популяции составляет от 36% до 44% с уровнем достоверности 95%.