Как рассчитать доверительный интервал для относительного риска

Относительный риск часто рассчитывается при анализе таблицы 2×2, которая имеет следующий формат:

Относительный риск говорит нам о вероятности возникновения события в экспериментальной группе по сравнению с вероятностью события в контрольной группе.

Он рассчитывается следующим образом:

• Относительный риск = [A/(A+B)] / [C/(C+D)]

Затем мы можем использовать следующую формулу для расчета доверительного интервала относительного риска (RR):

• ДИ менее 95% = e ^{ln(RR) – 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• ДИ более 95% = e ^{ln(RR) + 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

В следующем примере показано, как на практике рассчитать относительный риск и соответствующий доверительный интервал.

Пример: расчет доверительного интервала для относительного риска

Предположим, тренер по баскетболу использует новую программу тренировок, чтобы увидеть, увеличит ли она количество игроков, способных пройти определенный тест на навыки, по сравнению со старой программой тренировок.

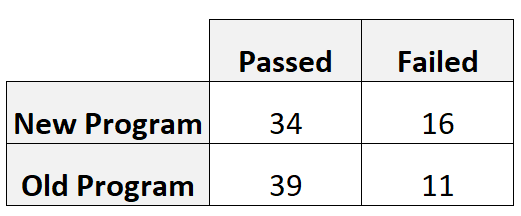
Тренер набирает 50 игроков для использования каждой программы. В следующей таблице показано количество игроков, прошедших и не прошедших тест на навыки, в зависимости от используемой ими программы:

Мы можем рассчитать относительный риск следующим образом:

• Относительный риск = [A/(A+B)] / [C/(C+D)]
• Относительный риск = [34/(34+16)] / [39/(39+11)]
• Относительный риск = 0,8718

Мы интерпретируем это так, что вероятность того, что игрок пройдет тест с использованием новой программы, всего в 0,8718 раза превышает вероятность того, что игрок пройдет тест с использованием старой программы.

Другими словами, вероятность прохождения игроком теста фактически снижается за счет использования новой программы.

Затем мы можем использовать следующие формулы для расчета 95% доверительного интервала для относительного риска:

• ДИ менее 95% = e ^{ln(0,8718) – 1,96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0,686
• ДИ более 95% = e ^{ln(0,8718) + 1,96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1,109

Таким образом, 95% доверительный интервал для относительного риска составляет [0,686, 1,109] .

Мы на 95% уверены, что истинный относительный риск между новой и старой программой обучения находится в пределах этого интервала.

Поскольку этот доверительный интервал содержит значение 1, он не является статистически значимым.

Это должно иметь смысл, если учесть следующее:

• Относительный риск больше 1 будет означать, что вероятность того, что игрок пройдет тест с использованием новой программы, больше , чем вероятность того, что игрок пройдет тест с использованием старой программы.
• Относительный риск меньше 1 будет означать, что вероятность прохождения игроком теста с использованием новой программы меньше , чем вероятность того, что игрок пройдет тест с использованием старой программы.

Итак, поскольку наш 95%-ный доверительный интервал для относительного риска содержит значение 1, это означает, что вероятность прохождения игроком теста навыков с использованием новой программы может быть или не быть больше, чем вероятность того, что тот же игрок пройдет тест с использованием новая программа. старая программа.

Дополнительные ресурсы

Следующие учебные пособия предоставляют дополнительную информацию об отношениях шансов и относительном риске:

Как интерпретировать отношения шансов
Как интерпретировать относительный риск
Как рассчитать соотношение шансов и относительный риск в Excel