Как создать доверительный интервал, используя распределение f
Чтобы определить, равны ли дисперсии двух совокупностей, мы можем вычислить коэффициент дисперсии σ 2 1 / σ 2 2 , где σ 2 1 — дисперсия совокупности 1, а σ 2 2 — дисперсия совокупности 2.
Чтобы оценить истинный коэффициент дисперсии генеральной совокупности, мы обычно берем простую случайную выборку из каждой совокупности и вычисляем коэффициент выборочной дисперсии, s 1 2 / s 2 2 , где s 1 2 и s 2 2 — выборочные дисперсии для выборки 1 и выборки. . 2 соответственно.
Этот тест предполагает, что s 1 2 и s 2 2 рассчитываются на основе независимых выборок размером n 1 и n 2 , как из нормально распределенных популяций.
Чем дальше это соотношение от единицы, тем сильнее доказательства неравных дисперсий внутри генеральной совокупности.
(1-α)100% доверительный интервал для σ 2 1 / σ 2 2 определяется как:
(s 1 2 / s 2 2 ) * F n 1 -1, n 2 -1, α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n 2 -1, n 1 -1, α/2
где F n 2 -1, n 1 -1, α/2 и F n 1 -1, n 2 -1, α/2 – критические значения распределения F для выбранного уровня значимости α.
Следующие примеры иллюстрируют, как создать доверительный интервал для σ 2 1 / σ 2 2 с помощью трех разных методов:
- За руку
- Используйте Microsoft Excel
- Использование статистического программного обеспечения R
Для каждого из следующих примеров мы будем использовать следующую информацию:
- α = 0,05
- п 1 = 16
- п2 = 11
- с 1 2 =28,2
- с 2 2 = 19,3
Создание доверительного интервала вручную
Чтобы вручную вычислить доверительный интервал для σ 2 1 / σ 2 2 , мы просто подставим имеющиеся у нас числа в формулу доверительного интервала:
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
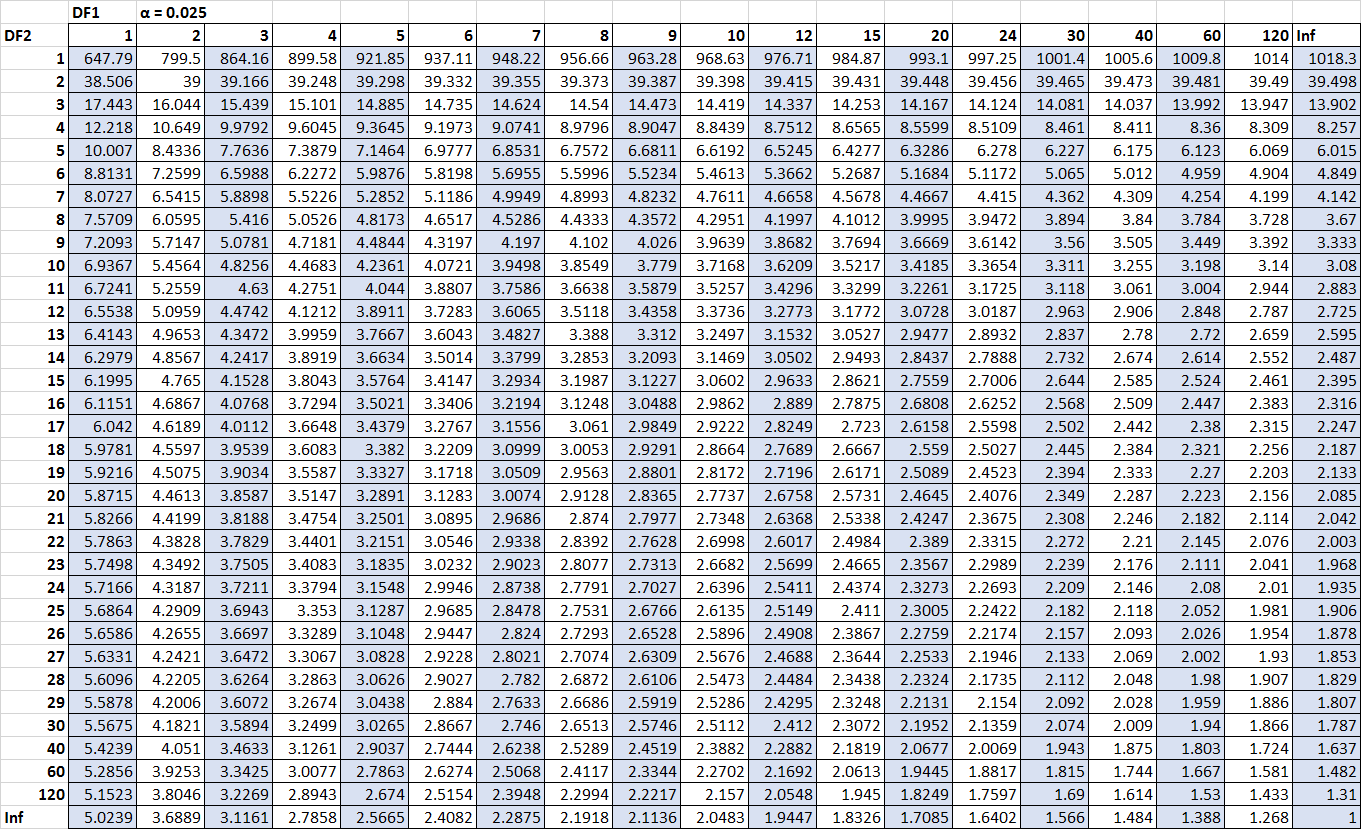
Единственные числа, которые нам не хватает, — это критические значения. К счастью, мы можем найти эти критические значения в таблице распределения F :
F n2-1, n1-1, α/2 = F 10, 15, 0,025 = 3,0602
F n1-1, n2-1, α/2 = 1/ F 15, 10, 0,025 = 1/3,5217 = 0,2839
(Нажмите, чтобы увеличить таблицу)
Теперь мы можем подставить все числа в интервал доверительной формулы:
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
(28,2/19,3) * (0,2839) ≤ σ 2 1 / σ 2 2 ≤ (28,2 / 19,3) * (3,0602)
0,4148 ≤ σ 2 1 / σ 2 2 ≤ 4,4714
Таким образом, 95% доверительный интервал для соотношения генеральных дисперсий равен (0,4148, 4,4714) .
Создание доверительного интервала с помощью Excel
На следующем изображении показано, как рассчитать 95% доверительный интервал для коэффициента дисперсии совокупности в Excel. Нижний и верхний пределы доверительного интервала показаны в столбце E, а формула, используемая для определения нижнего и верхнего пределов, показана в столбце F:
Таким образом, 95% доверительный интервал для соотношения генеральных дисперсий равен (0,4148, 4,4714) . Это соответствует тому, что мы получили, когда вручную рассчитали доверительный интервал.
Создание доверительного интервала с помощью R
Следующий код показывает, как вычислить 95% доверительный интервал для соотношения генеральных дисперсий в R:
#define significance level, sample sizes, and sample variances alpha <- .05 n1 <- 16 n2 <- 11 var1 <- 28.2 var2 <- 19.3 #define F critical values upper_crit <- 1/qf(alpha/2, n1-1, n2-1) lower_crit <- qf(alpha/2, n2-1, n1-1) #find confidence interval lower_bound <- (var1/var2) * lower_crit upper_bound <- (var1/var2) * upper_crit #output confidence interval paste0("(", lower_bound, ", ", upper_bound, " )") #[1] "(0.414899337980266, 4.47137571035219 )"
Таким образом, 95% доверительный интервал для соотношения генеральных дисперсий равен (0,4148, 4,4714) . Это соответствует тому, что мы получили, когда вручную рассчитали доверительный интервал.
Дополнительные ресурсы
Как читать распределительную плату F
Как найти критическое значение F в Excel