Древовидная диаграмма

В этой статье объясняется, что такое древовидная диаграмма и как она создается. Таким образом, вы найдете примеры древовидных структур, преимущества этого типа диаграмм и, кроме того, упражнение, решаемое шаг за шагом.

Что такое дерево?

Древовидная диаграмма , также называемая деревом вероятностей , представляет собой графическое представление всех возможных результатов эксперимента вместе с их вероятностями.

Таким образом, древовидная диаграмма используется для отображения всех возможных результатов в выборочном пространстве и расчета их вероятностей.

Древовидная диаграмма построена таким образом, что каждый результат ( узел ) разветвляется на новые возможные результаты ( ветви ), пока не будут достигнуты окончательные результаты.

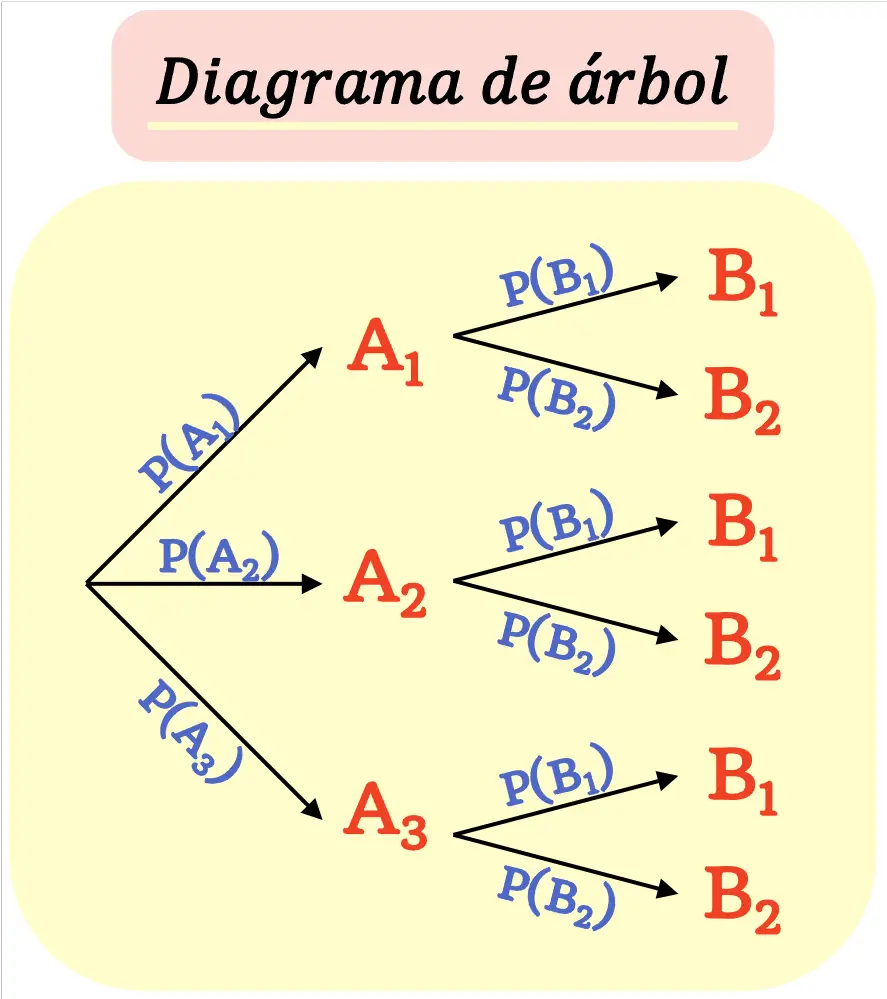
Следует иметь в виду, что сумма вероятностей всех ветвей, выходящих из узла, должна быть равна 1.

Как сделать древовидную диаграмму

Для создания дерева необходимо выполнить следующие шаги:

1. Первым шагом в создании древовидной диаграммы является рисование ветвей для каждого возможного результата. Это будут филиалы первого поколения.
2. Затем вероятность, связанная с каждым событием, добавляется к соответствующей ветви.
3. Конец каждой ветви первого поколения представляет собой узел, из которого должны быть представлены ветви последующих возможных событий.
4. Как и в первых ветках, мы должны сложить вероятности представленных событий.
5. Повторяйте шаги 3 и 4, пока не дойдете до конечных узлов, то есть возможных окончаний эксперимента.

Обратите внимание, что количество ветвей на одном уровне не обязательно должно равняться количеству ветвей на другом уровне. Аналогичным образом, количество ответвлений, возникающих в результате возможного результата, может варьироваться даже в пределах одного и того же уровня.

Пример дерева

Теперь, когда мы знаем определение и теорию создания древовидной диаграммы, давайте шаг за шагом рассмотрим реальный пример, чтобы лучше понять концепцию.

• Постройте дерево вероятностей броска трех независимых монет. Затем определите вероятность того, что при всех трех бросках выпадет решка.

При жеребьевке возможны только два результата: мы можем получить орел или решку. Следовательно, вероятность выпадения орла или решки при подбрасывании монеты равна:

Как только мы узнаем вероятности возможных результатов, мы приступим к представлению древовидной диаграммы.

Поскольку подбрасывания монеты независимы, вероятность выпадения орла или решки всегда будет одинаковой для каждого броска. Следовательно, для построения дерева должны быть представлены две ветви (орёл и решка) с одинаковой вероятностью для каждого сделанного броска.

И как только мы построили дерево, все, что нам нужно сделать, это определить вероятность того, что выпадет три монеты.

Следовательно, в данном случае мы должны перемножить все вероятности выпадения орла, ведь это вероятности того пути, который приведет нас к желаемому результату.

Таким образом, вероятность выпадения орла при трех бросках монеты рассчитывается следующим образом:

Короче говоря, вероятность выпадения орла три раза подряд составляет 12,5%.

Решенное упражнение с деревом

В деревне всего 3 ясля: 60% детей ходят в ясли А, 30% — в ясли Б и 10% — в ясли С. Кроме того, в трех яслях 55% населения — девочки. Постройте дерево и рассчитайте следующие вероятности:

• Вероятность того, что случайно выбранный ребенок окажется девочкой из детского сада B.
• Вероятность того, что из любого детского сада случайно выберут ребенка, и это будет мальчик.

Обратите внимание: если доля девочек во всех детских садах составляет 55%, процент мальчиков рассчитывается простым вычитанием 1 минус 0,55:

Теперь, когда мы знаем все вероятности, мы можем создать дерево вероятностей со всеми возможностями:

Таким образом, вероятность случайного выбора девочки из детского сада B рассчитывается следующим образом:

С другой стороны, чтобы определить вероятность выбора мальчика в любом детском саду, мы должны сначала найти вероятность выбора мальчика для каждого детского сада, а затем сложить их:

Преимущества древовидной структуры

Благодаря особенностям древовидной структуры преимущества этого типа статистического графика заключаются в следующем:

• Древовидные диаграммы очень полезны для принятия решений.
• Взаимосвязь между всеми возможными исходами можно представить графически.
• Очень удобно найти первопричину проблемы.
• Облегчает решение вероятностных и статистических задач.
• Древовидная диаграмма помогает систематизировать идеи и проанализировать ситуацию.