Закон бенфорда
В этой статье объясняется, что такое закон Бенфорда. Кроме того, вы сможете увидеть, как был открыт закон Бенфорда и каковы применения этого статистического закона.
Что такое Закон Бенфорда?
Закон Бенфорда , также называемый законом первой цифры , представляет собой статистический закон, который гласит, что вероятность того, что первая цифра фрагмента данных равна 1, больше, чем вероятность того, что это другое число.
Другими словами, закон Бенфорда гласит, что в наборе числовых данных, существующих в реальной жизни, число 1 является наиболее повторяющимся числом в качестве первой цифры данных.
Кроме того, чем выше число, тем меньше вероятность, что он окажется на первом месте. Следовательно, первое число скорее будет 1, чем 2, но 2 более вероятно, чем 3, 3 более вероятно, чем 4, и так далее.
Закон Бенфорда обязан своим названием американцу Фрэнку Бенфорду. Хотя Бенфорд и не изобрел его, он популяризировал это статистическое правило. Ниже мы увидим происхождение закона Бенфорда.
Формула закона Бенфорда
Закон Бенфорда гласит, что вероятность того, что первая цифра представляет собой определенное число, равна логарифму одного плюс один по этому числу.
Таким образом , формула закона Бенфорда выглядит следующим образом:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
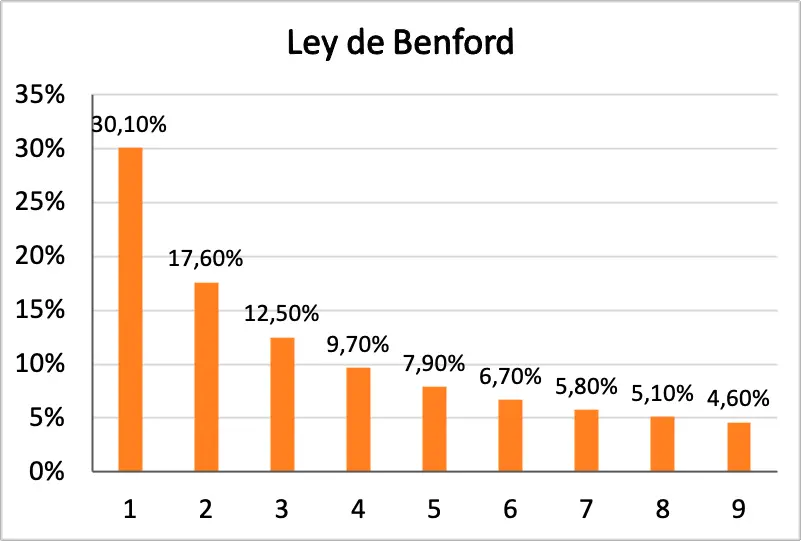
Следовательно, из формулы закона Бенфорда мы можем вывести вероятность для каждого числа того, что оно является первой цифрой элемента данных. В следующей таблице вы можете увидеть проценты всех вероятностей:
| Фигура | Вероятность того, что быть первым номером |
|---|---|
| 1 | 30,1% |
| 2 | 17,6% |
| 3 | 12,5% |
| 4 | 9,7% |
| 5 | 7,9% |
| 6 | 6,7% |
| 7 | 5,8% |
| 8 | 5,1% |
| 9 | 4,6% |
Дополнительно ниже вы можете увидеть гистограмму, на которой графически представлены все вероятности закона Бенфорда:
История закона Бенфорда
В 1881 году математик Саймон Ньюкомб вывел закон Бенфорда, когда обнаружил, что первые страницы таблиц логарифмов используются значительно чаще, чем последние. Это означало, что первые цифры чисел не одинаково вероятны, но что 1 встречается чаще, чем 2, 2 чаще, чем 3, и так до 9.
Однако Ньюкомб не оставил никаких статистических доказательств того, что это правило соблюдалось, он просто сделал вывод из износа логарифмических таблиц.
Позже, а именно в 1938 году, физик Фрэнк Бенфорд сделал то же наблюдение, а также провел эксперимент, чтобы проверить его эмпирически. На наборе статистических данных, состоящем из 20 229 значений из 20 различных образцов, он провел исследование первой цифры каждого данных. Итак, на основе результатов он продемонстрировал выполнение закона Бенфорда и вывел формулу, которая позволила ему вычислить вероятность того, что первая цифра будет определенным числом (эту формулу мы видели выше).
Короче говоря, хотя закон Бенфорда был впервые открыт Саймоном Ньюкомбом, он назван в честь Фрэнка Бенфорда, потому что именно он подтвердил этот статистический закон.
Применение закона Бенфорда
Закон Бенфорда — это статистический закон, который находит применение в самых разных областях. Например, закон Бенфорда широко используется в экономике, биологии и даже политике.
В экономике закон Бенфорда часто используется для обнаружения манипулирования данными, поскольку, если набор данных не соответствует закону Бенфорда, это указывает на то, что данными манипулировали. Этот закон, например, используется для выявления возможных случаев налогового мошенничества.
Следует отметить, что закон Бенфорда не используется для доказательства истинности случайных явлений, поскольку результаты равновероятны. Таким образом, правило Бенфорда нельзя использовать для проверки результатов лотереи.
С другой стороны, в генетике закон Бенфорда можно использовать для анализа различий в длине генома между разными типами организмов.
Наконец, были также предприняты попытки обнаружить фальсификации результатов голосования с помощью закона Бенфорда, хотя его полезность в данном случае подвергалась сомнению.