Как интерпретировать отношения шансов
В статистике вероятность относится к шансам наступления события. Он рассчитывается следующим образом:
ВЕРОЯТНОСТЬ:
P(событие) = (# желаемых результатов) / (# возможных результатов)
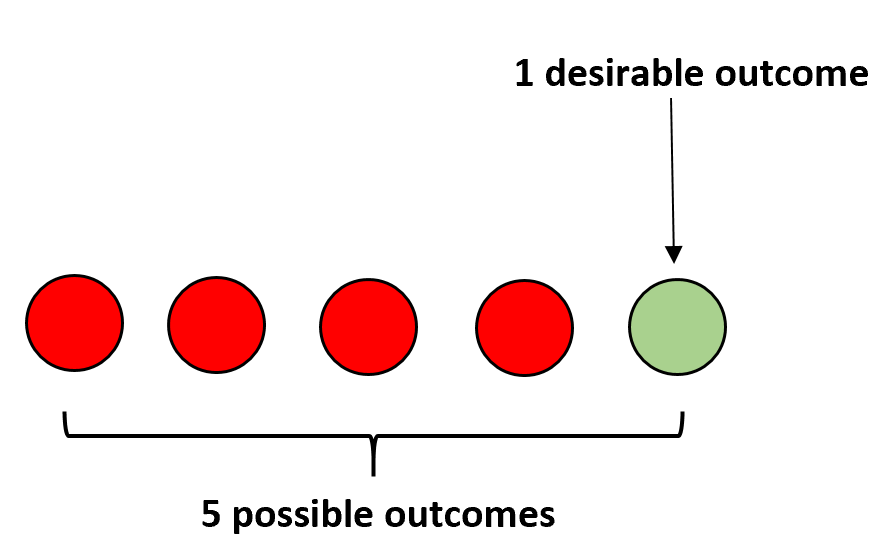
Например, предположим, что у нас в мешке четыре красных и один зеленый шар. Если вы закроете глаза и наугад выберете шар, вероятность того, что вы выберете зеленый шар, рассчитывается следующим образом:
P(зеленый) = 1/5 = 0,2 .
Вероятность наступления события можно рассчитать следующим образом:
ШАНСЫ:
Шансы (событие) = P (событие происходит) / 1-P (событие происходит)
Например, вероятность попадания зеленого мяча равна (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .
Отношение шансов – это отношение двух вероятностей.
ОТЧЕТ УДАЧИ:
Коэффициент шансов = Шансы на событие A / Шансы на событие B
Например, мы могли бы вычислить отношение шансов между выбором красного и зеленого шаров.
Вероятность вытянуть красный шар равна 4/5 = 0,8 .
Шансы вытащить красный шар равны (0,8)/1-(0,8) = 0,8/0,2 = 4 .
Отношение шансов на выбор красного шара над зеленым рассчитывается следующим образом:
Коэффициенты (красный)/Коэффициенты (зеленый) = 4/0,25 = 16 .
Таким образом, вероятность попадания красного мяча в 16 раз превышает вероятность попадания зеленого мяча.
Когда отношения шансов используются в реальном мире?
В реальном мире отношения шансов используются в различных контекстах, когда исследователи хотят сравнить шансы наступления двух событий. Вот некоторые примеры.
Пример №1: Интерпретация отношений шансов
Исследователи хотят знать, повышает ли новое лечение шансы пациента на положительный результат в отношении здоровья по сравнению с существующим лечением. В следующей таблице показано количество пациентов, у которых наблюдался положительный или отрицательный результат в отношении здоровья, в зависимости от лечения.

Шансы на положительный результат применения нового лечения у пациента можно рассчитать следующим образом:
Шансы = P(положительный) / 1 – P(положительный) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25
Вероятность того, что пациент получит положительный результат при существующем лечении, можно рассчитать следующим образом:
Шансы = P(положительный) / 1 – P(положительный) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875
Таким образом, отношение шансов достижения положительного результата при новом лечении по сравнению с существующим лечением можно рассчитать следующим образом:
Отношение шансов = 1,25/0,875 = 1,428 .
Мы интерпретируем это как означающее, что шансы пациента на положительный результат при использовании нового лечения в 1,428 раза превышают шансы пациента на положительный результат при использовании существующего лечения.
Другими словами, благодаря новому лечению шансы на положительный результат увеличиваются на 42,8% .
Пример №2: Интерпретация отношений шансов
Маркетологи хотят знать, заставляет ли реклама покупателей покупать данный товар чаще, чем другая реклама. Таким образом, они показывают каждое объявление 100 людям. В следующей таблице показано количество людей, купивших товар, на основе просмотренной ими рекламы:
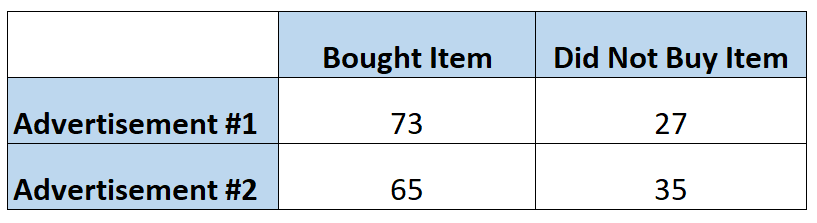
Шансы на то, что человек купит товар после просмотра первого объявления, можно рассчитать следующим образом:
Коэффициенты = P(куплено) / 1 – P(куплено) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704
Шансы на то, что человек купит товар после просмотра второго объявления, можно рассчитать следующим образом:
Коэффициенты = P(куплено) / 1 – P(куплено) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857
Таким образом, соотношение шансов покупки товара после просмотра первой рекламы по сравнению с покупкой после просмотра второй рекламы можно рассчитать следующим образом:
Отношение шансов = 2,704/1,857 = 1,456 .
Мы интерпретируем это так, что вероятность того, что человек купит товар после просмотра первого объявления, в 1,456 раза превышает вероятность того , что человек купит товар после просмотра второго объявления.
Другими словами, шансы на покупку товара увеличиваются на 45,6% благодаря первому листингу.
Дополнительные ресурсы
Как рассчитать соотношение шансов и относительный риск в Excel
Как интерпретировать отношение шансов меньше 1
Как интерпретировать относительный риск