Как выполнить квантильную регрессию в python
Линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между одной или несколькими переменными-предикторами и переменной отклика .
Обычно, когда мы выполняем линейную регрессию, мы хотим оценить среднее значение переменной ответа.
Однако вместо этого мы могли бы использовать метод, известный как квантильная регрессия , для оценки любого значения квантиля или процентиля значения ответа, например 70-го процентиля, 90-го процентиля, 98-го процентиля и т. д.
В этом руководстве представлен пошаговый пример использования этой функции для выполнения квантильной регрессии в Python.
Шаг 1. Загрузите необходимые пакеты
Сначала загрузим необходимые пакеты и функции:
import numpy as np import pandas as pd import statsmodels. api as sm import statsmodels. formula . api as smf import matplotlib. pyplot as plt
Шаг 2. Создайте данные
Для этого примера мы создадим набор данных, содержащий учебные часы и результаты экзаменов, полученные для 100 студентов университета:
#make this example reproducible n.p. random . seeds (0) #create dataset obs = 100 hours = np. random . uniform (1, 10, obs) score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100) df = pd. DataFrame ({' hours ':hours, ' score ':score}) #view first five rows df. head () hours score 0 5.939322 68.764553 1 7.436704 77.888040 2 6.424870 74.196060 3 5.903949 67.726441 4 4.812893 72.849046
Шаг 3. Выполните квантильную регрессию
Далее мы подберем модель квантильной регрессии, используя часы обучения в качестве предикторной переменной и результаты экзаменов в качестве переменной ответа.
Мы будем использовать модель для прогнозирования ожидаемого 90-го процентиля результатов экзамена на основе количества изученных часов:
#fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )
#view model summary
print ( model.summary ())
QuantReg Regression Results
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
Model: 1
==================================================== ============================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================
Из результата мы можем увидеть предполагаемое уравнение регрессии:
90-й процентиль экзаменационного балла = 59,6104 + 2,8495*(часы)
Например, 90-й процентиль всех студентов, обучающихся 8 часов, должен составлять 82,4:
90-й процентиль экзаменационного балла = 59,6104 + 2,8495*(8) = 82,4 .
Выходные данные также отображают верхний и нижний доверительные пределы для точки пересечения и времени переменной-предиктора.
Шаг 4. Визуализируйте результаты
Мы также можем визуализировать результаты регрессии, создав диаграмму рассеяния с подобранным уравнением квантильной регрессии, наложенным на график:
#define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))
#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])
#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)
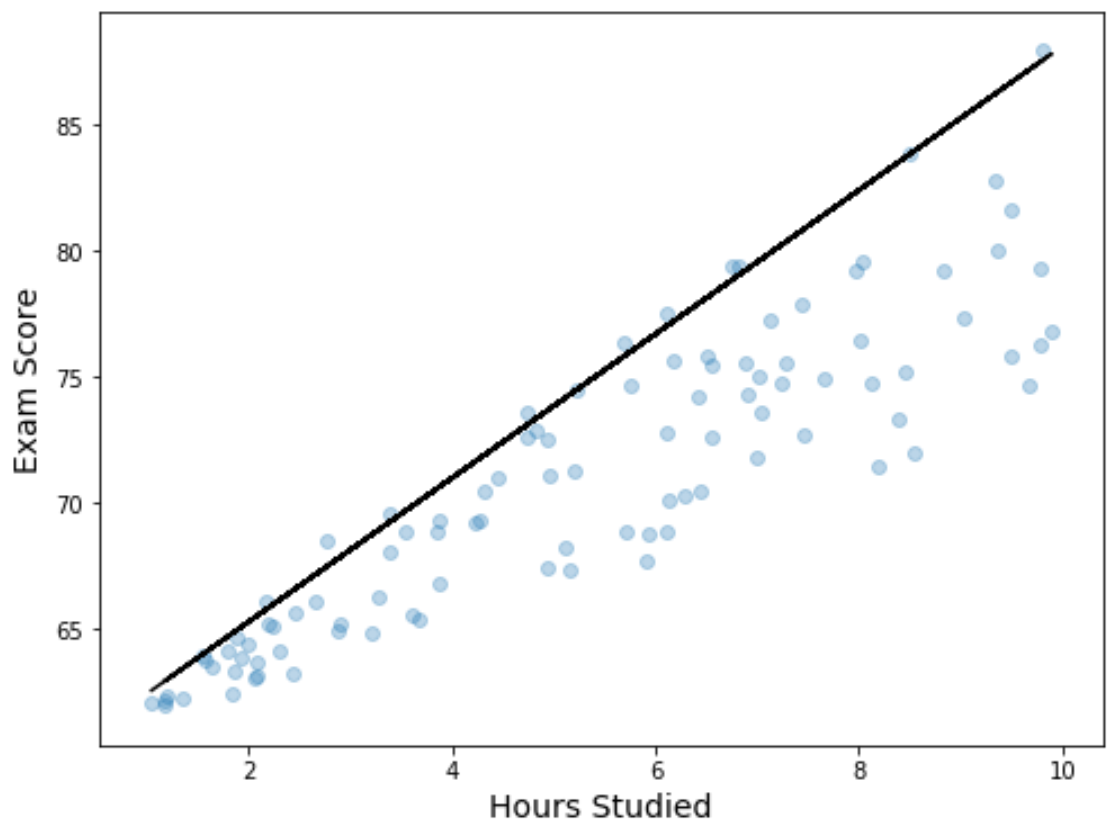
В отличие от простой линии линейной регрессии, обратите внимание, что эта подобранная линия не представляет собой «линию наилучшего соответствия» данным. Вместо этого он проходит через расчетный 90-й процентиль на каждом уровне предикторной переменной.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Python
Как выполнить квадратичную регрессию в Python