Корреляционная матрица
В этой статье вы узнаете, что такое корреляционная матрица, какова ее формула и как ее интерпретировать. Дополнительно вы сможете увидеть конкретный пример интерпретации корреляционной матрицы.
Что такое корреляционная матрица?
Матрица корреляции — это матрица, которая содержит в позиции i,j коэффициент корреляции между переменными i и j .
Следовательно, матрица корреляции представляет собой квадратную матрицу, заполненную единицами на главной диагонали, а элемент строки i и столбца j состоит из значения коэффициента корреляции между переменной i и переменной j .
Таким образом , формула корреляционной матрицы выглядит следующим образом:

Золото
![]()
– коэффициент корреляции между переменными
![]()
И
![]()
Итак, чтобы найти матрицу корреляции набора данных, важно знать, как рассчитывается коэффициент корреляции. Если вы не помните, по следующей ссылке вы узнаете, как это сделать с помощью онлайн-калькулятора:
Свойством коэффициента корреляции является то, что порядок переменных не имеет значения для его расчета, то есть коэффициент корреляции
![]()
эквивалентно
![]()
Следовательно, корреляционная матрица симметрична.
![Rendered by QuickLaTeX.com \displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-76d9753ac0f42dcdc12ea4b719f37750_l3.png)
Чтобы матрица корреляции имела смысл, набор статистических данных должен содержать более двух переменных. В противном случае было бы достаточно определить один коэффициент корреляции, и матрица корреляции имела бы смысл.
Как составить корреляционную матрицу
Учитывая определение корреляционной матрицы, давайте посмотрим, как создается этот тип статистической матрицы:
- Рассчитайте коэффициент корреляции каждой пары переменных. Обратите внимание, что порядок переменных не меняет результат, поэтому его нужно вычислять только один раз для каждой пары переменных.
- Создайте квадратную матрицу той же размерности, что и количество переменных в ряду данных. Эта матрица будет корреляционной матрицей.
- Поставьте 1 в каждый элемент главной диагонали корреляционной матрицы.
- Поместите коэффициент корреляции переменных i , j в позиции i , j и j , i .
- После того как корреляционная матрица создана, остается только интерпретировать ее значения.
Имейте в виду, что просто запустить корреляционную матрицу недостаточно, нужно потом интерпретировать ее значения и понять, что они означают. В следующем разделе объясняется, как интерпретировать корреляционную матрицу.
Интерпретация корреляционной матрицы
Для правильной интерпретации корреляционной матрицы необходимо учитывать, что значение коэффициента корреляции может находиться в пределах от -1 до +1:
- r=-1 : две переменные имеют идеальную отрицательную корреляцию, поэтому мы можем нарисовать линию с отрицательным наклоном, в которой все точки соединяются.
- -1<r<0 : корреляция между двумя переменными отрицательна, поэтому, когда одна переменная увеличивается, другая уменьшается. Чем ближе значение к -1, тем более отрицательно связаны переменные.
- r=0 : корреляция между двумя переменными очень слабая, фактически линейная связь между ними равна нулю. Это не означает, что переменные независимы, поскольку они могут иметь нелинейную связь.
- 0<r<1 : корреляция между двумя переменными положительна, чем ближе значение к +1, тем сильнее связь между переменными. В этом случае одна переменная имеет тенденцию увеличивать свое значение, когда увеличивается и другая.
- r=1 : две переменные имеют идеальную положительную корреляцию, то есть имеют положительную линейную связь.
Таким образом, для интерпретации корреляционной матрицы необходимо интерпретировать каждый коэффициент корреляции и сравнить разные результаты.
Таким образом вы сможете увидеть, какие переменные больше всего связаны друг с другом, какие переменные наиболее важны, какие переменные практически не связаны друг с другом и т. д.
Пример корреляционной матрицы
Чтобы полностью понять, из чего состоит корреляционная матрица и как она интерпретируется, в этом разделе мы разберем пример корреляционной матрицы:
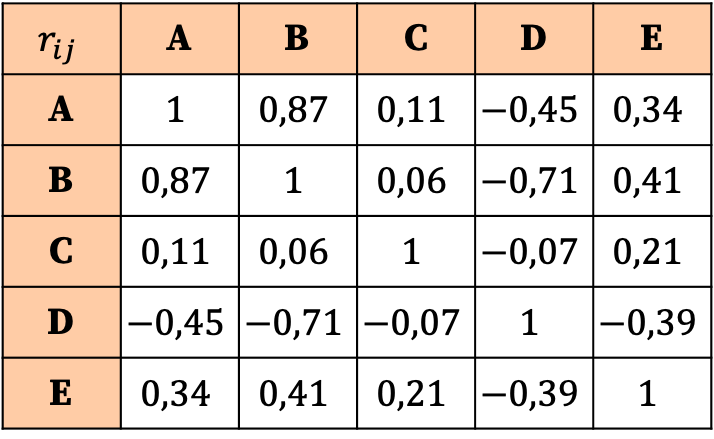
Интерпретация корреляционной матрицы основана на значениях коэффициентов. Таким образом, мы видим, что самой сильной корреляцией является связь между переменной A и переменной B, поскольку соответствующий ей коэффициент является наибольшим (0,87).
С другой стороны, переменная С практически не имеет корреляции ни с одной переменной, поскольку все ее коэффициенты очень близки к нулю и поэтому очень малы. Таким образом, чтобы упростить анализ, мы могли бы даже рассмотреть возможность исключения этой переменной из статистического исследования.
Аналогично, все связи переменной D с другими переменными отрицательны, а это означает, что корреляция между переменной D и другими переменными обратная. Это не означает, что переменную следует исключить, просто переменная D имеет отрицательную корреляцию.
Как видите, матрица корреляции очень полезна для обобщения данных и проведения общего анализа взаимосвязей между различными переменными в наборе данных.