Как создать матрицу корреляции в google sheets
Один из способов количественной оценки связи между двумя переменными – использовать коэффициент корреляции Пирсона , который является мерой линейной связи между двумя переменными . Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
Но в некоторых случаях мы хотим понять корреляцию между несколькими парами переменных. В этих случаях мы можем создать матрицу корреляции , которая представляет собой квадратную таблицу, показывающую коэффициенты корреляции между несколькими парными комбинациями переменных.
В этом руководстве объясняется, как создать и интерпретировать корреляционную матрицу в Google Sheets.
Как создать матрицу корреляции в Google Sheets
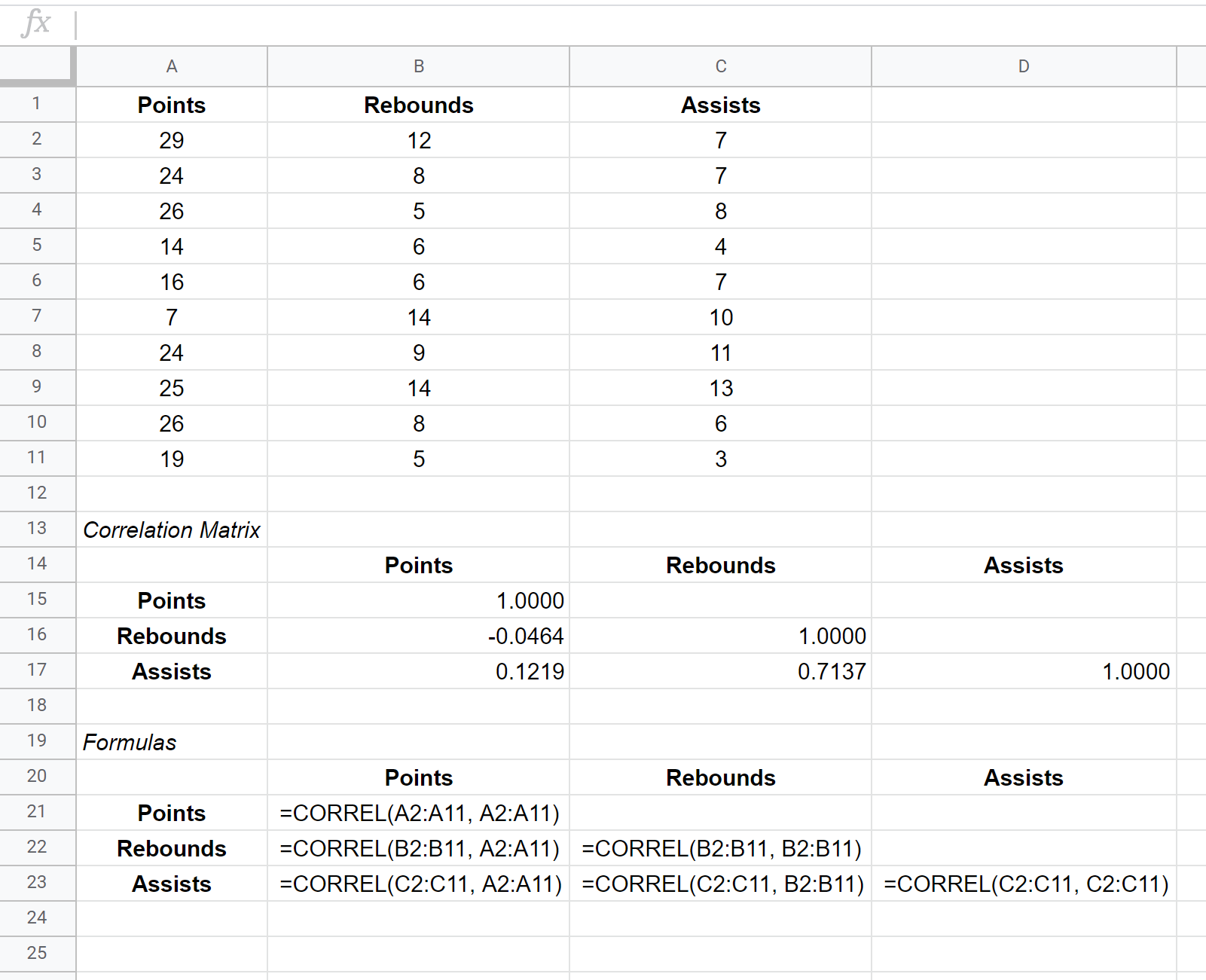
Допустим, у нас есть следующий набор данных, который показывает среднее количество очков, подборов и передач для 10 баскетболистов:
Чтобы создать корреляционную матрицу для этого набора данных, мы можем использовать функцию КОРРЕЛ() со следующим синтаксисом:
КОВАР(данные_y, данные_x)
Ковариационная матрица для этого набора данных показана в ячейках B15:D17 , а формулы, использованные для создания ковариационной матрицы, показаны в ячейках B21:D23 ниже:
Как интерпретировать корреляционную матрицу
Значения в отдельных ячейках корреляционной матрицы говорят нам коэффициент корреляции Пирсона между каждой парной комбинацией переменных. Например:
Соотношение очков и подборов: -0,0464. Очки и подборы слегка отрицательно коррелируют, но это значение настолько близко к нулю, что нет убедительных доказательств значимой связи между этими двумя переменными.
Соотношение очков и передач: 0,1219. Очки и передачи слегка коррелируют положительно, но это значение также довольно близко к нулю, поэтому убедительных доказательств значимой связи между этими двумя переменными нет.
Соотношение подборов и передач: 0,7137. Подборы и передачи сильно положительно коррелируют. То есть игроки, у которых больше подборов, также, как правило, делают больше передач.
Обратите внимание, что все диагональные значения корреляционной матрицы равны 1, поскольку корреляция между переменной и самой собой всегда равна 1. На практике это число бесполезно для интерпретации.
Дополнительные ресурсы
Как читать корреляционную матрицу
Как создать матрицу корреляции в Excel