Как создать и интерпретировать матрицу корреляции в excel

Один из способов количественной оценки взаимосвязи между двумя переменными состоит в использовании коэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными .

Он имеет значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
• 0 указывает на отсутствие линейной корреляции между двумя переменными.
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.

Но в некоторых случаях мы хотим понять корреляцию между несколькими парами переменных.

В этих случаях мы можем создать матрицу корреляции , которая представляет собой квадратную таблицу, показывающую коэффициенты корреляции между несколькими парными комбинациями переменных.

В этом руководстве объясняется, как создать и интерпретировать корреляционную матрицу в Excel.

Как создать матрицу корреляции в Excel

Допустим, у нас есть следующий набор данных, который показывает среднее количество очков, подборов и передач для 10 баскетболистов:

Чтобы создать корреляционную матрицу для этого набора данных, перейдите на вкладку «Данные» на верхней ленте Excel и нажмите «Анализ данных» .

Если вы не видите эту опцию, вам необходимо сначала загрузить бесплатный пакет инструментов анализа данных в Excel .

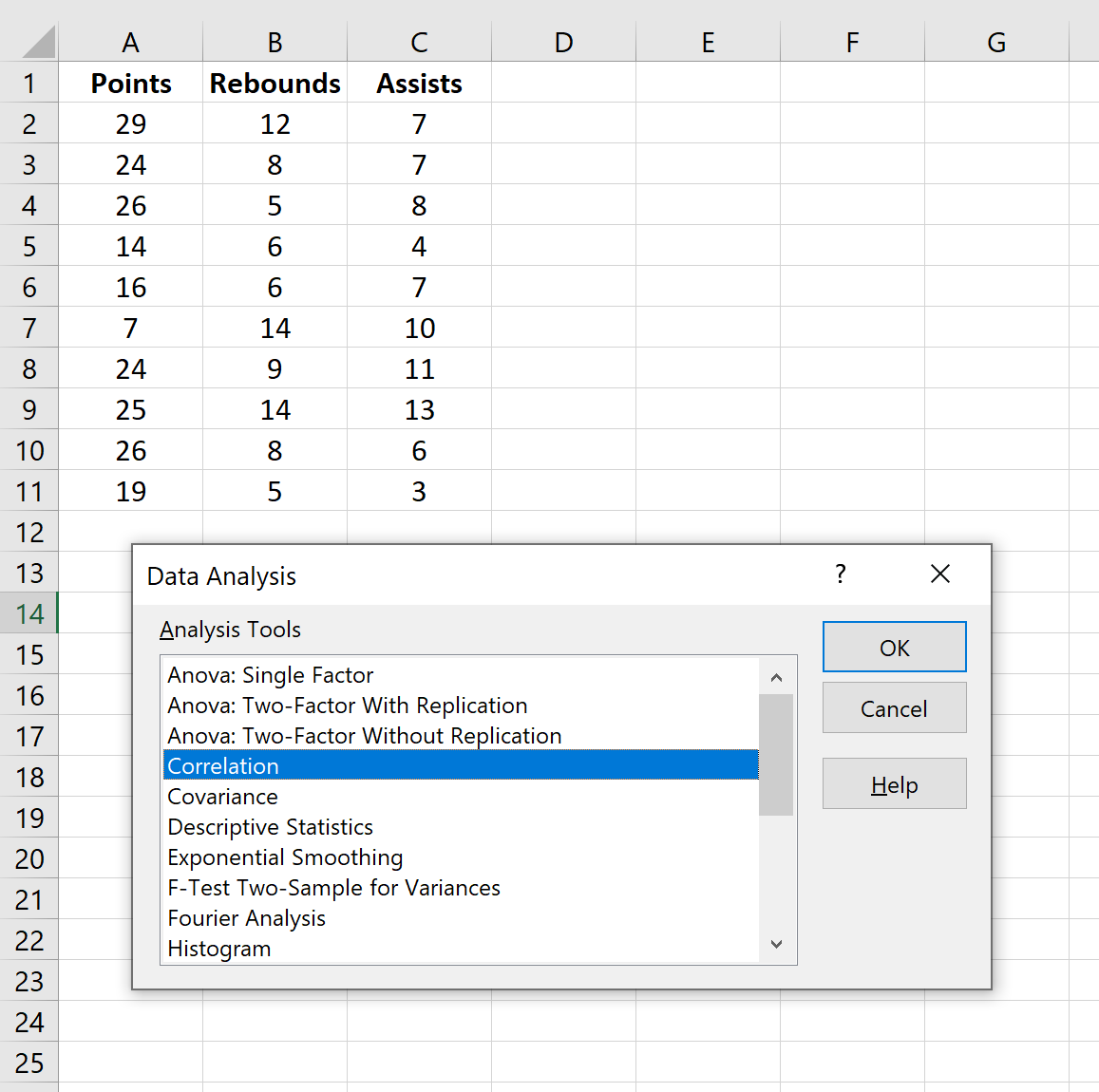
В появившемся новом окне выберите «Корреляция» и нажмите «ОК» .

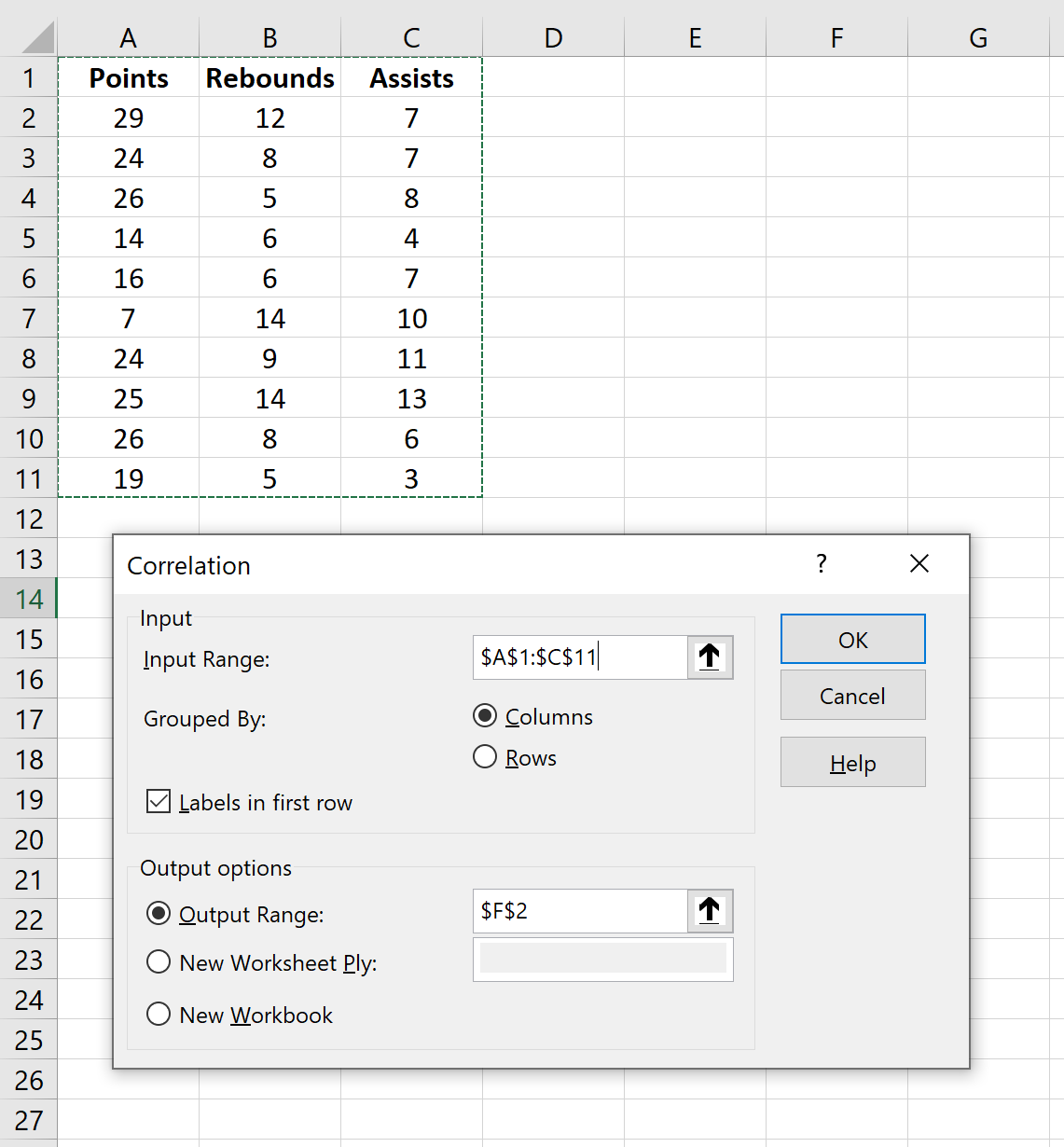
В поле «Диапазон ввода» выберите ячейки, в которых расположены данные (включая первую строку с метками). Установите флажок «Ярлыки в первой строке» . В поле «Выходной диапазон» выберите ячейку, в которой вы хотите, чтобы отображалась корреляционная матрица. Затем нажмите ОК .

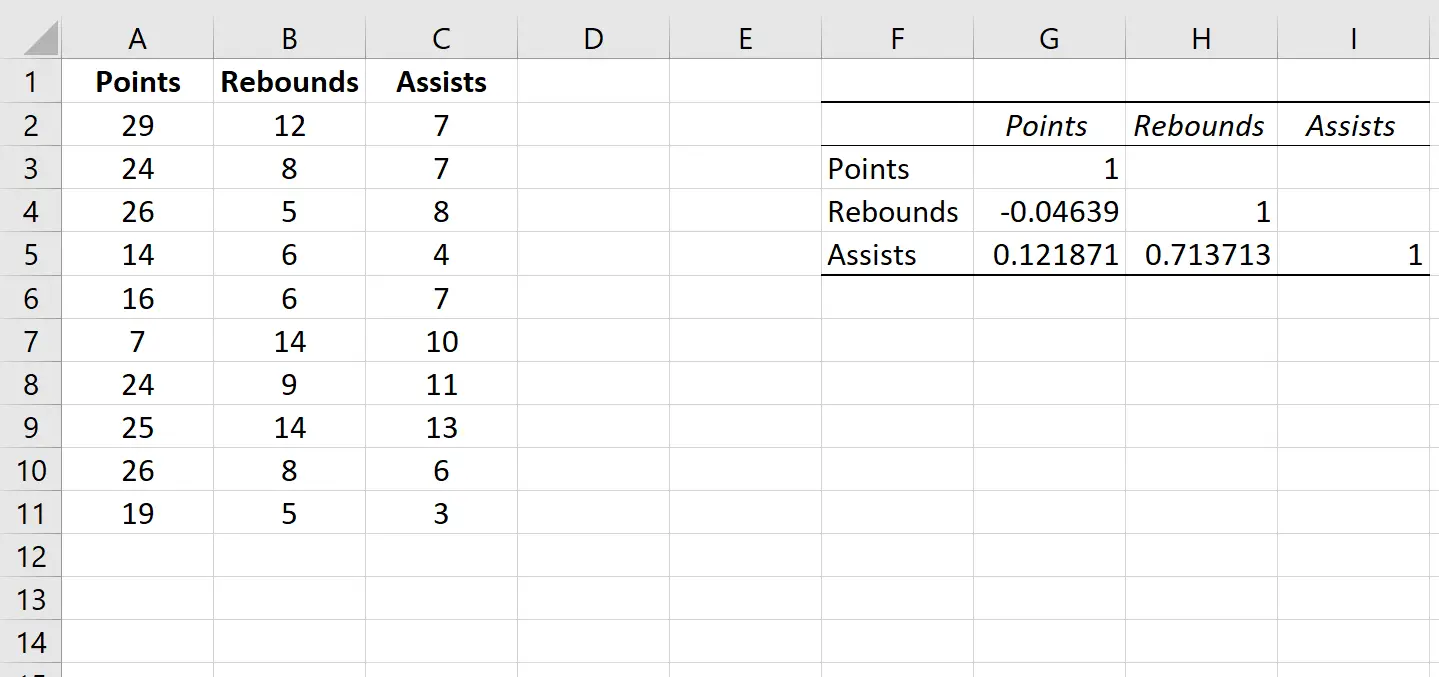
Это автоматически создаст следующую корреляционную матрицу:

Как интерпретировать корреляционную матрицу в Excel

Значения в отдельных ячейках корреляционной матрицы говорят нам о коэффициенте корреляции Пирсона между каждой парной комбинацией переменных. Например:

Соотношение очков и подборов: -0,04639. Очки и подборы слегка отрицательно коррелируют, но это значение настолько близко к нулю, что нет убедительных доказательств значимой связи между этими двумя переменными.

Соотношение очков и передач: 0,121871. Очки и передачи слегка положительно коррелируют, но это значение также довольно близко к нулю, поэтому убедительных доказательств значимой связи между этими двумя переменными нет.

Соотношение подборов и передач: 0,713713. Подборы и передачи сильно положительно коррелируют. То есть игроки, у которых больше подборов, также, как правило, делают больше передач.

Обратите внимание, что все диагональные значения корреляционной матрицы равны 1, поскольку корреляция между переменной и самой собой всегда равна 1. На практике это число бесполезно для интерпретации.

Бонус: визуализируйте коэффициенты корреляции

Простой способ визуализировать значения коэффициентов корреляции в таблице — применить к таблице условное форматирование .

На верхней ленте Excel перейдите на вкладку «Главная» , затем группу «Стили» .

Нажмите «Диаграмма условного форматирования» , затем «Цветовые шкалы» , затем «Зелено-желто-красная цветовая шкала» .

При этом к корреляционной матрице автоматически применяется следующая цветовая шкала:

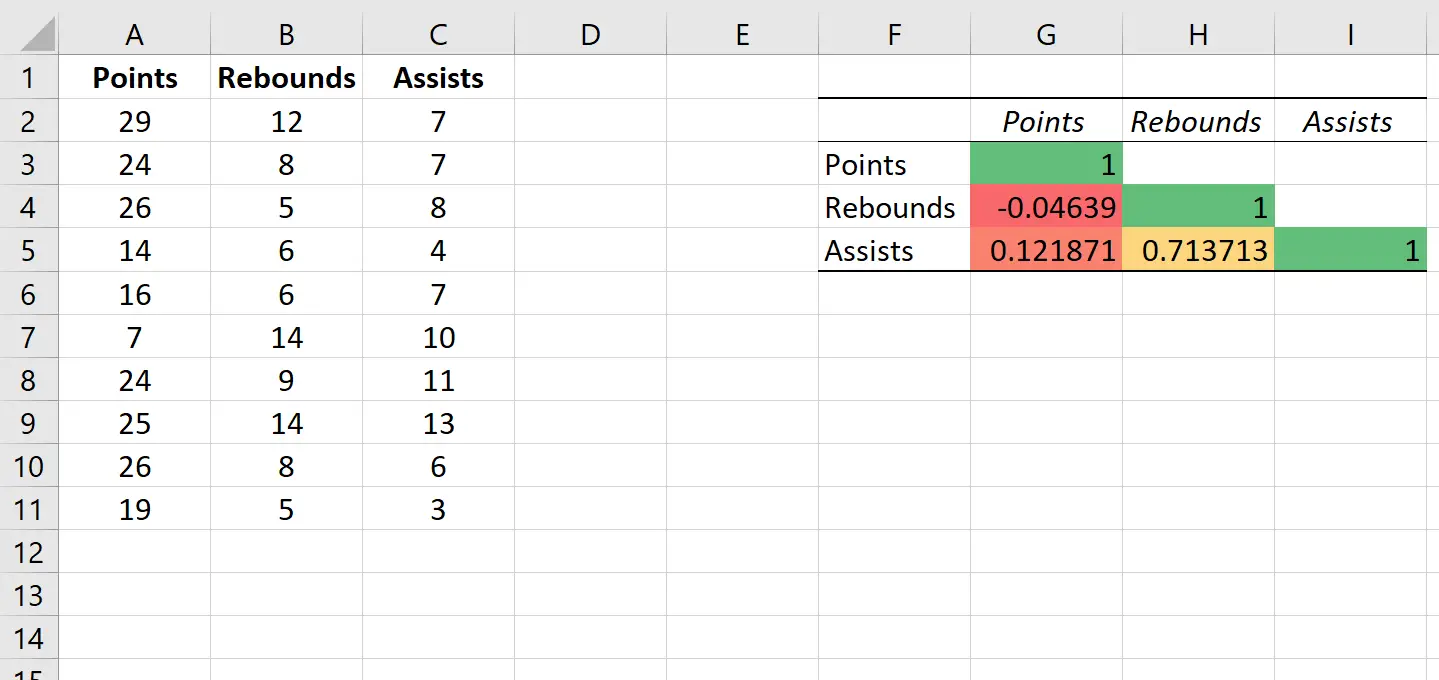
Это помогает нам легко визуализировать силу корреляций между переменными.

Это особенно полезный совет, если мы работаем с корреляционной матрицей со многими переменными, поскольку он помогает нам быстро определить переменные, которые имеют наиболее сильную корреляцию.

Связанный: Что считается «сильной» корреляцией?

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:

Как создать матрицу точечной диаграммы в Excel
Как выполнить корреляционный тест в Excel