Как рассчитать корреляцию между категориальными переменными

Мы часто используем коэффициент корреляции Пирсона для расчета корреляции между непрерывными числовыми переменными.

Однако нам нужно использовать другую метрику для расчета корреляции между категориальными переменными, то есть переменными, которые имеют имена или метки, такие как:

• Семейное положение (холост, женат, разведен)
• Статус курения (курящий, некурящий)
• Цвет глаз (голубой, карий, зеленый)

Для расчета корреляции между категориальными переменными обычно используются три меры:

1. Тетрахорическая корреляция: используется для расчета корреляции между двоичными категориальными переменными.

2. Полихорическая корреляция: используется для расчета корреляции между порядковыми категориальными переменными.

3. V Крамера: используется для расчета корреляции между номинальными категориальными переменными.

В следующих разделах приведен пример расчета каждого из этих трех измерений.

Метрика 1: Тетрахорическая корреляция

Тетрахорическая корреляция используется для расчета корреляции между двоичными категориальными переменными. Помните, что двоичные переменные — это переменные, которые могут принимать только одно из двух возможных значений.

Значение тетрахорической корреляции варьируется от -1 до 1, где -1 указывает на сильную отрицательную корреляцию, 0 указывает на отсутствие корреляции, а 1 указывает на сильную положительную корреляцию.

Например, предположим, что мы хотим знать, связан ли пол с предпочтением той или иной политической партии. Поэтому мы берем простую случайную выборку из 100 избирателей и спрашиваем их об их предпочтениях в отношении той или иной политической партии.

В следующей таблице представлены результаты опроса:

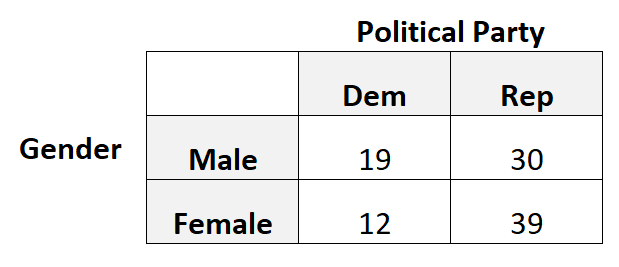
В этом сценарии мы бы использовали тетрахорную корреляцию, поскольку каждая категориальная переменная является бинарной, то есть каждая переменная может принимать только два возможных значения.

Мы можем использовать следующий код в R для расчета тетрахорической корреляции между двумя переменными:

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

Тетрахорная корреляция оказывается равной 0,27 . Это значение довольно низкое, что указывает на слабую (если таковую) связь между полом и предпочтениями политических партий.

Метрика 2: Полихорическая корреляция

Полихорическая корреляция используется для расчета корреляции между порядковыми категориальными переменными. Напомним, что порядковые переменные — это переменные, возможные значения которых имеют естественный порядок.

Значение полихорической корреляции варьируется от -1 до 1, где -1 указывает на сильную отрицательную корреляцию, 0 указывает на отсутствие корреляции, а 1 указывает на сильную положительную корреляцию.

Например, предположим, что вы хотите узнать, имеют ли два разных рейтинговых агентства высокую корреляцию между рейтингами фильмов.

Мы просим каждое агентство оценить 20 различных фильмов по шкале от 1 до 3, где 1 означает «плохо», 2 — «плохо», а 3 — «хорошо».

В следующей таблице показаны результаты:

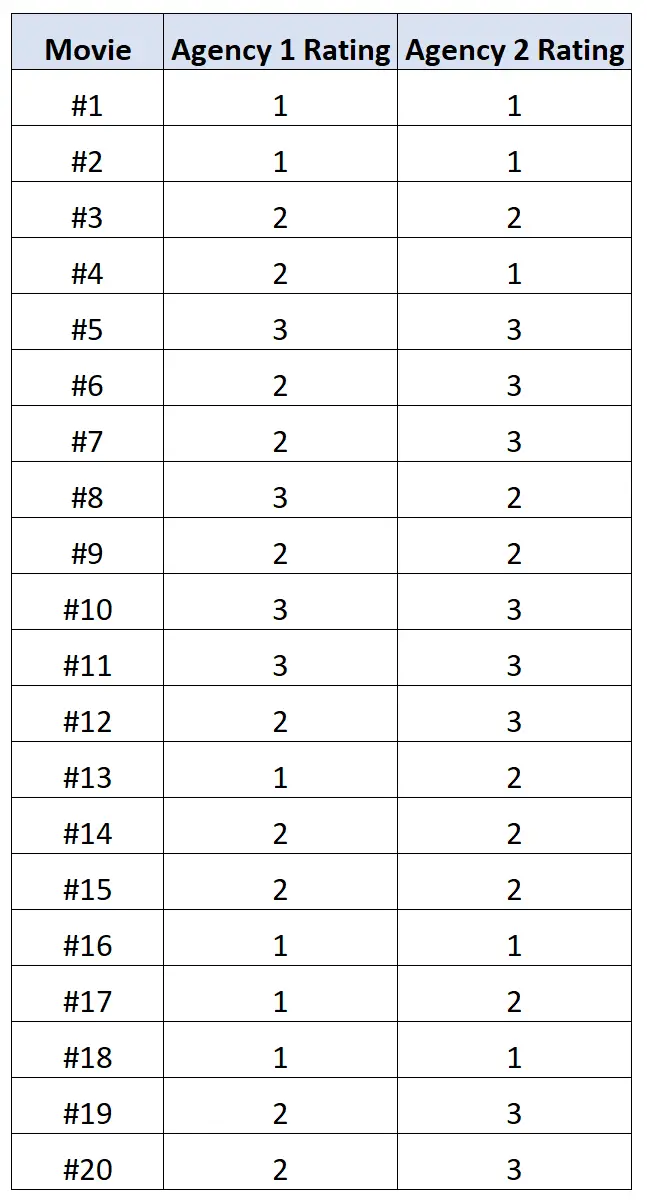
Мы можем использовать следующий код на языке R для расчета полихорической корреляции между рейтингами двух агентств:

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

Полихорическая корреляция оказывается равной 0,78 . Это значение довольно высокое, что указывает на сильную положительную связь между рейтингами каждого агентства.

Показатель 3: V Крамера

V Крамера используется для расчета корреляции между номинальными категориальными переменными. Помните, что номинальные переменные — это те, которые имеют метки категорий, но не имеют естественного порядка.

Значение V Крамера варьируется от 0 до 1, где 0 указывает на отсутствие связи между переменными, а 1 указывает на сильную связь между переменными.

Например, предположим, что мы хотим знать, существует ли корреляция между цветом глаз и полом. Поэтому мы опросили 50 человек и получили следующие результаты:

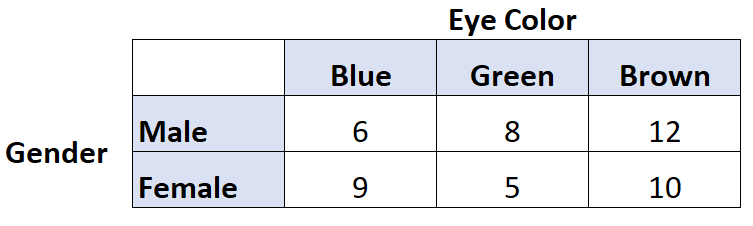
Мы можем использовать следующий код в R для расчета V Крамера для этих двух переменных:

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

V Крамера оказывается равным 0,1671 . Это значение довольно низкое, что указывает на слабую связь между полом и цветом глаз.

Дополнительные ресурсы

Введение в коэффициент корреляции Пирсона
Введение в тетрахорическую корреляцию
Категориальные или количественные переменные: в чем разница?
Уровни измерения: номинальный, порядковый, интервальный и коэффициентный.