Коэффициент внутриклассовой корреляции: определение + пример

Коэффициент внутриклассовой корреляции (ICC) используется для измерения надежности оценок в исследованиях, в которых участвуют два или более оценщика.

Значение ICC может варьироваться от 0 до 1, где 0 указывает на отсутствие надежности среди оценщиков, а 1 указывает на идеальную надежность среди оценщиков.

Проще говоря, ICC используется для определения того, могут ли элементы (или темы) быть надежно оценены разными экспертами.

Существует несколько различных версий ICC, которые можно рассчитать в зависимости от следующих трех факторов:

• Модель: односторонние случайные эффекты, двусторонние случайные эффекты или двусторонние смешанные эффекты.
• Тип отношений: последовательность или абсолютное согласие.
• Единица измерения: один оценщик или среднее значение оценщиков.

Вот краткое описание трех различных моделей :

1. Модель односторонних случайных эффектов. Эта модель предполагает, что каждый предмет оценивается отдельной группой случайно выбранных оценщиков. В этой модели оценщики считаются источником случайных эффектов. Эта модель редко используется на практике, поскольку для оценки каждого предмета обычно используется одна и та же группа экспертов.

2. Модель двусторонних случайных эффектов. Эта модель предполагает, что группа оценщиков k случайно выбирается из совокупности и затем используется для оценки испытуемых. Используя эту модель, оценщики и испытуемые считаются источниками случайных эффектов. Эта модель часто используется, когда мы хотим распространить наши результаты на оценщиков, аналогичных тем, которые использовались в исследовании.

3. Двусторонняя модель смешанных эффектов. Эта модель также предполагает, что группа оценщиков k случайно выбирается из совокупности и затем используется для оценки испытуемых. Однако эта модель предполагает, что группа оценщиков, которую мы выбрали, является единственными оценщиками, представляющими интерес, а это означает, что мы не хотим обобщать наши результаты на других оценщиков, которые также могут иметь схожие характеристики с оценщиками, использованными в исследовании.

Вот краткое описание двух разных типов отношений, которые мы можем измерить:

1. Последовательность: нас интересуют систематические различия между оценками судей (например, оценили ли судьи схожие темы как низкие или высокие?)

2. Абсолютное согласие: нас интересуют абсолютные различия между оценками судей (например, какова абсолютная разница между оценками судьи А и судьи Б?)

Вот краткое описание двух разных модулей , которые могут нас заинтересовать:

1. Один рецензент. Мы хотим использовать оценки только одного рецензента в качестве основы для измерения.

2. Среднее значение оценщика. Мы хотим использовать среднее значение оценок всех судей в качестве основы для измерения.

Примечание. Если вы хотите измерить уровень согласия между двумя оценщиками, которые пропустили каждый из пунктов дихотомического результата , вместо этого вам следует использовать каппу Коэна .

Как интерпретировать коэффициент внутриклассовой корреляции

Вот как интерпретировать значение коэффициента внутриклассовой корреляции, по мнению Ку и Ли :

• Менее 0,50: низкая надежность.
• От 0,5 до 0,75: средняя надежность.
• Между 0,75 и 0,9: хорошая надежность.
• Больше 0,9: отличная надежность.

В следующем примере показано, как на практике рассчитать коэффициент внутриклассовой корреляции.

Пример: расчет коэффициента внутриклассовой корреляции

Предположим, четырех разных судей просят оценить качество 10 различных вступительных экзаменов в колледж. Результаты показаны ниже:

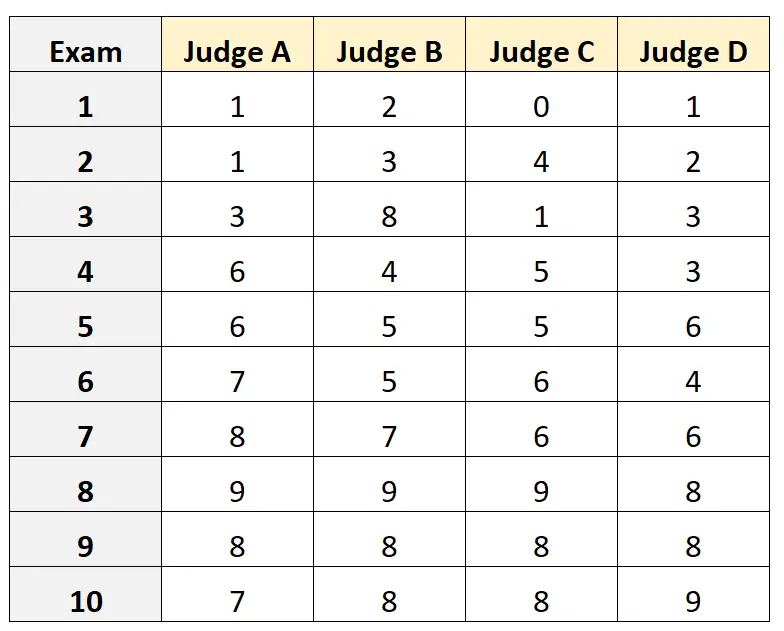
Предположим, что четыре судьи были случайным образом выбраны из группы квалифицированных судей для вступительного экзамена, и мы хотели измерить абсолютное согласие между судьями и использовать оценки с точки зрения только одного оценщика в качестве основы для нашего измерения.

Мы можем использовать следующий код на R, чтобы подогнать модель двусторонних случайных эффектов , используя абсолютное согласие в качестве отношения между оценщиками и используя одну единицу в качестве интересующей единицы:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

Коэффициент внутриклассовой корреляции (ICC) оказался равным 0,782 .

Основываясь на практических правилах интерпретации ICC, мы пришли к выводу, что ICC, равный 0,782, указывает на то, что экзамены могут быть оценены с «хорошей» надежностью разными экспертами.

Дополнительные ресурсы

В следующих руководствах представлены подробные объяснения того, как рассчитать ICC в различных статистических программах:

Как рассчитать коэффициент внутриклассовой корреляции в Excel
Как рассчитать коэффициент внутриклассовой корреляции в R
Как рассчитать коэффициент внутриклассовой корреляции в Python