Линия регрессии

К бенджамин андерсон 2 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое линия регрессии в статистике. Итак, вы найдете, как рассчитать линию регрессии между двумя переменными, решенное упражнение и, кроме того, онлайн-калькулятор для расчета линии регрессии для любой выборки данных.

Что такое линия регрессии?

В статистике линия регрессии — это линия, полученная на основе простой модели линейной регрессии . Точнее, линия регрессии — это линия, которая лучше всего соответствует диаграмме рассеяния и, следовательно, лучше всего описывает набор статистических данных.

Таким образом, уравнение линии регрессии математически связывает независимую переменную X и зависимую переменную Y набора данных. Хотя линия регрессии обычно не способна точно определить значение каждого наблюдения, она может дать приблизительную оценку его значения.

Как вы можете видеть на предыдущем графике, линия регрессии помогает нам увидеть тенденцию набора данных и тип связи между независимой переменной и зависимой переменной. Ниже мы рассмотрим применение линии регрессии.

Формула линии регрессии

Теперь, когда мы знаем определение линии регрессии, давайте посмотрим, как рассчитать уравнение линии модели линейной регрессии.

Как и любая линия, уравнение линии регрессии состоит из константы (b ₀ ) и наклона (b ₁ ):

$y=b_0+b_1x$

Таким образом, формулы расчета коэффициентов линии линейной регрессии имеют следующий вид:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

Золото:

$b_0$

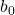
– константа линии регрессии.
$b_1$

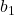
– наклон линии регрессии.
$x_i$

— значение независимой переменной X данных i.
$y_i$

— значение зависимой переменной Y данных i.
$\overline{x}$

представляет собой среднее значение независимой переменной
$\overline{y}$

представляет собой среднее значение зависимой переменной Y.

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать линию регрессии для любого набора данных.

Конкретный пример линии регрессии

Чтобы глубже изучить концепцию линии регрессии, ниже приведен рабочий пример того, как создать линию регрессии.

После сдачи статистического экзамена пятерым студентам был задан вопрос, сколько учебных часов они потратили на экзамен, данные приведены в таблице ниже. Рассчитайте линию регрессии на основе собранных статистических данных, чтобы линейно связать часы обучения с полученной оценкой. Далее определите, какую оценку получит ученик, проучившийся 8 часов.

Чтобы найти линию регрессии для выборочных данных, нам нужно определить коэффициенты b ₀ и b ₁ уравнения, и для этого нам нужно использовать формулы, представленные в разделе выше.

Однако, чтобы применить формулы для линии линейной регрессии, мы должны сначала вычислить среднее значение независимой переменной и среднее значение зависимой переменной:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Теперь, когда мы знаем средние значения переменных, мы вычисляем коэффициент b ₁ модели, используя соответствующую формулу:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Наконец, мы вычисляем коэффициент b ₀ модели, используя соответствующую формулу:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Вкратце, уравнение линии линейной регрессии задачи выглядит следующим образом:

$y=2,0294+0,4412x$

Ниже вы можете увидеть графическое представление выборочных данных, а также прямую линию простой модели линейной регрессии:

После того, как мы рассчитали линию регрессии, чтобы спрогнозировать оценку, которую получит студент, проучившийся 8 часов, просто подставьте это значение в уравнение полученной линии регрессии:

$y=2,0294+0,4412\cdot 8=5,56$

Таким образом, согласно проведенной модели линейной регрессии, если студент учился восемь часов, он получит на экзамене балл 5,56.

Для чего используется линия регрессии?

В основном линия регрессии имеет два применения: линия регрессии используется для определения типа связи между двумя переменными и, с другой стороны, линия регрессии также позволяет вам сделать прогноз относительно значения нового наблюдения.

Наклон линии регрессии говорит нам, какова корреляция между независимой переменной и зависимой переменной. Если наклон положительный, это означает, что зависимая переменная прямо пропорциональна независимой переменной, а если наклон отрицательный, это означает, что переменные обратно пропорциональны. Наконец, если коэффициент наклона очень близок к нулю, это означает, что корреляция между двумя переменными очень слабая.

Кроме того, если уравнение линии регрессии известно, значение зависимой переменной можно спрогнозировать для нового значения независимой переменной, как мы это сделали в примере выше. Таким образом, чем лучше адаптирована линия регрессии, тем точнее прогнозы она дает.

Калькулятор линии регрессии

Введите образец данных в следующий калькулятор, чтобы рассчитать линию регрессии между двумя переменными. Вам необходимо разделить пары данных так, чтобы в первом поле были только значения независимой переменной X, а во втором поле — только значения зависимой переменной Y.

Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше