Логистическая регрессия против линейной регрессии: основные различия
Двумя наиболее часто используемыми моделями регрессии являются линейная регрессия и логистическая регрессия .
Оба типа регрессионных моделей используются для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика , но между этими двумя моделями есть несколько ключевых отличий:
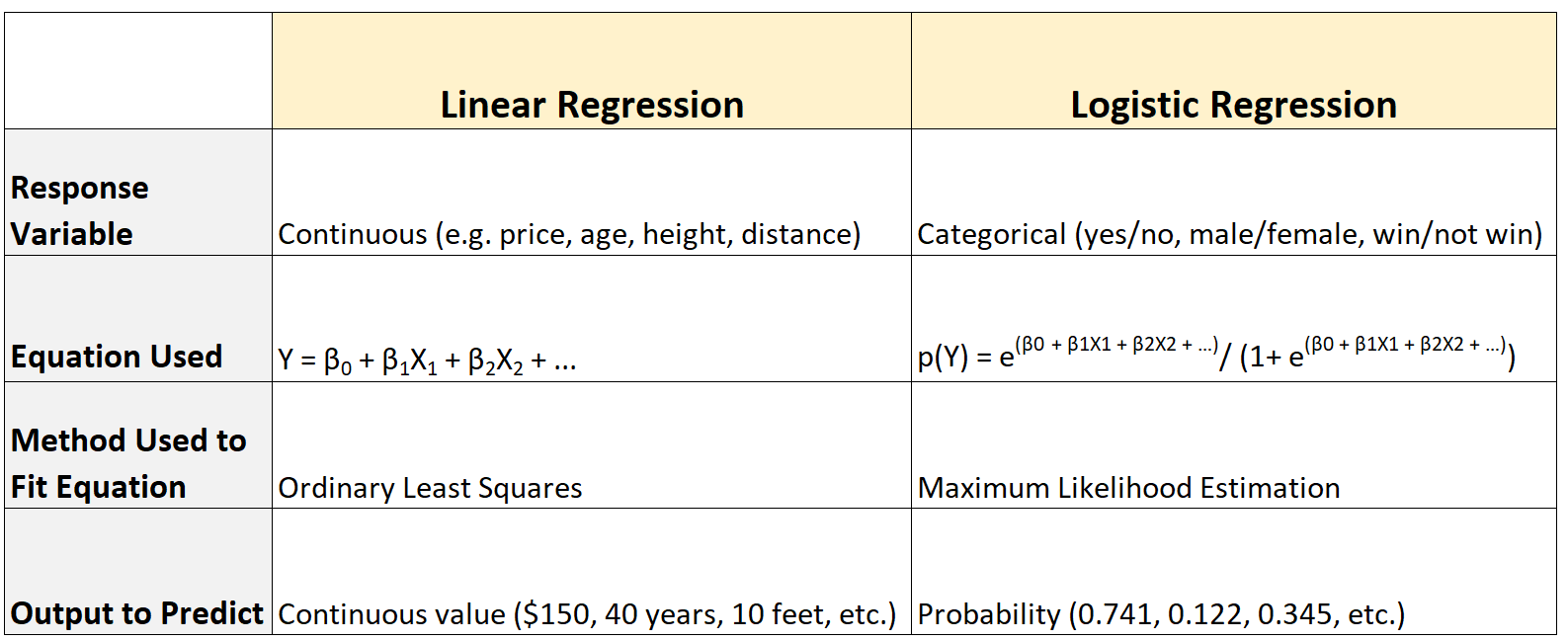
Вот краткое описание различий:
Отличие №1: Тип переменной ответа
Модель линейной регрессии используется, когда переменная отклика принимает непрерывное значение, такое, что:
- Цена
- Высота
- Возраст
- Расстояние
И наоборот, модель логистической регрессии используется, когда переменная ответа принимает категориальное значение, например:
- Да или нет
- Мужчина или женщина
- Выиграть или не выиграть
Отличие №2: используется уравнение
Линейная регрессия использует следующее уравнение для суммирования взаимосвязи между переменными-предикторами и переменной ответа:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
Золото:
- Y: переменная ответа
- X j : j- я прогнозируемая переменная
- β j : Среднее влияние на Y увеличения X j на одну единицу, при этом все остальные предикторы остаются фиксированными.
И наоборот, логистическая регрессия использует следующее уравнение:
p(X) = e β 0 + β 1 X 1 + β 2 X 2 + … + β p
Это уравнение используется для прогнозирования вероятности того, что отдельное наблюдение попадает в определенную категорию.
Отличие №3: метод, используемый для решения уравнения
Линейная регрессия использует метод, известный как обычные наименьшие квадраты, для поиска наиболее подходящего уравнения регрессии.
И наоборот, логистическая регрессия использует метод, известный как оценка максимального правдоподобия, для поиска наиболее подходящего уравнения регрессии.
Отличие № 4: результат должен быть спрогнозирован
Линейная регрессия прогнозирует непрерывное значение в качестве результата. Например:
- Цена (150, 199, 400 и т. д.)
- Рост (14 дюймов, 2 фута, 94,32 сантиметра и т. д.)
- Возраст (2 месяца, 6 лет, 41,5 года и т.д.)
- Расстояние (1,23 мили, 4,5 километра и т. д.)
И наоборот, логистическая регрессия прогнозирует вероятности как результат. Например:
- Шанс поступления в университет составляет 40,3%.
- Вероятность победы в игре 93,2%.
- Вероятность того, что закон будет принят, составляет 34,2%.
Когда использовать логистическую или линейную регрессию
Следующие практические задачи помогут вам лучше понять, когда использовать логистическую регрессию или линейную регрессию.
Проблема №1: Годовой доход
Предположим, экономист хочет использовать переменные-предикторы (1) количество отработанных часов в неделю и (2) годы обучения, чтобы спрогнозировать годовой доход людей.
В этом сценарии он будет использовать линейную регрессию , поскольку переменная ответа (годовой доход) является непрерывной.
Проблема № 2: поступление в колледж
Предположим, сотрудник приемной комиссии колледжа хочет использовать переменные-предсказатели (1) средний балл и (2) балл ACT, чтобы спрогнозировать вероятность того, что студент будет принят в определенный университет.
В этом сценарии она будет использовать логистическую регрессию , поскольку переменная ответа является категориальной и может принимать только два значения: принято или не принято.
Проблема №3: Цены на недвижимость
Предположим, агент по недвижимости хочет использовать переменные-предсказатели (1) площадь в квадратных футах, (2) количество спален и (3) количество ванных комнат, чтобы спрогнозировать цены продажи дома.
В этом сценарии она будет использовать линейную регрессию , поскольку переменная ответа (цена) является непрерывной.
Проблема № 4: Обнаружение спама
Предположим, программист хочет использовать переменные-предсказатели (1) количество слов и (2) страну происхождения, чтобы предсказать вероятность того, что данное электронное письмо является спамом.
В этом сценарии будет использоваться логистическая регрессия , поскольку переменная ответа является категориальной и может принимать только два значения: спам или не спам.
Дополнительные ресурсы
Следующие руководства содержат более подробную информацию о линейной регрессии:
- Введение в простую линейную регрессию
- Введение в множественную линейную регрессию
- 4 примера использования линейной регрессии в реальной жизни
Следующие руководства предлагают более подробную информацию о логистической регрессии:
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше