Ковариационная матрица
В этой статье объясняется, что такое ковариационная матрица и какова ее формула. На конкретном примере вы узнаете, как создать ковариационную матрицу, и узнаете о свойствах ковариационной матрицы.
Что такое ковариационная матрица?
Ковариационная матрица представляет собой квадратную матрицу, элементами которой являются дисперсии и ковариации изучаемых переменных. Таким образом, элементы главной диагонали ковариационной матрицы представляют собой дисперсию каждой переменной, а остальные элементы — ковариации между переменными.
В статистике ковариационная матрица используется для анализа взаимосвязи между двумя и более случайными величинами. Ковариационная матрица очень полезна, поскольку позволяет быстро интерпретировать корреляцию между многими переменными, поскольку вы можете видеть значения всех ковариаций переменных одновременно.
Обозначением ковариационной матрицы является заглавная греческая буква сигма (Σ).
Как рассчитать ковариационную матрицу
Для расчета ковариационной матрицы нескольких статистических переменных необходимо выполнить следующие шаги:
- Вычислите дисперсии всех переменных.
- Вычислите ковариацию каждой пары переменных.
- Сформируйте ковариационную матрицу:
- Дисперсия переменной i должна располагаться на главной диагонали матрицы, точнее в позиции i,i .
- Ковариация между переменными i и j должна быть помещена в позиции i,j матрицы.
Таким образом, формула ковариационной матрицы выглядит следующим образом:
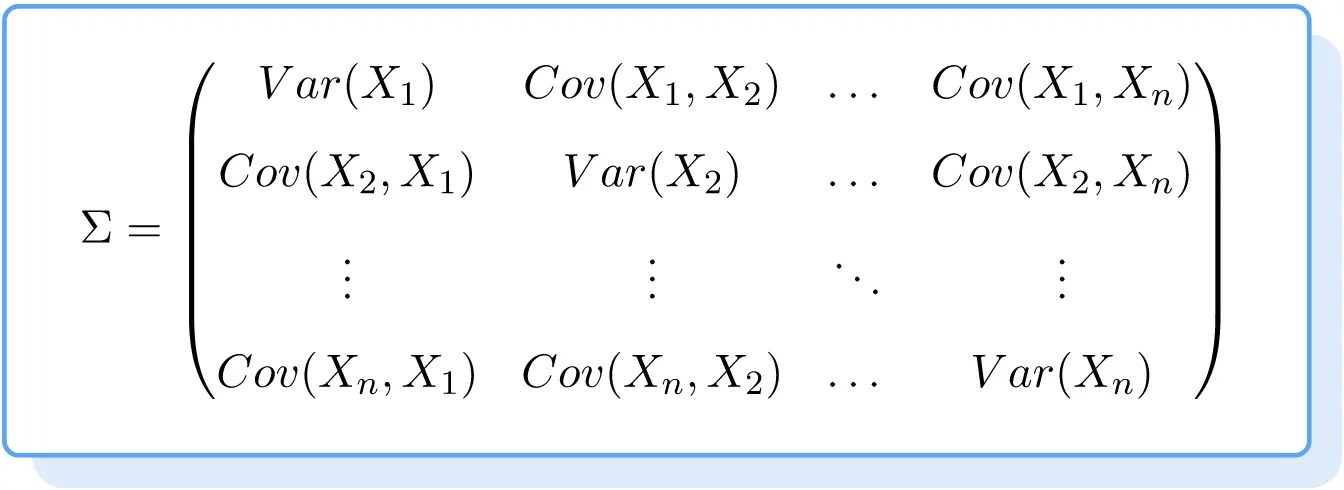
Пример ковариационной матрицы
После ознакомления с определением ковариационной матрицы ниже приведено пошаговое упражнение, чтобы вы могли увидеть, как создается матрица этого типа.
Вычисляет ковариационную матрицу переменных X, Y и Z, значения которой:
- Х: 4, 7, 12, 5, 7
- И: 9, 15, 19, 6, 8.
- З: 7, 2, 4, 6, 3
Первое, что нам нужно сделать, это определить дисперсии всех переменных:
![]()
![]()
![]()
Во-вторых, мы находим ковариацию между каждой парой переменных:
![]()
![]()
![]()
И как только мы вычислили все дисперсии и ковариации, остается только составить ковариационную матрицу. Для этого поместим значения дисперсии на главную диагональ матрицы, а значения ковариации в соответствующую им позицию:
![Rendered by QuickLaTeX.com \Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3a423b40ad6d25b57327b1f3dccd5df4_l3.png)
![Rendered by QuickLaTeX.com \Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d90c58cc3c8ecef6a85c88196e1dd08d_l3.png)
Как видите, представляя дисперсии и ковариации в матрице, переменные очень легко интерпретировать. Переменной с наибольшей дисперсией является Y (23,44), с другой стороны, переменные X и Y имеют прямую связь, а переменные X и Z (и, следовательно, Y и Z) имеют обратную связь.
Обратите внимание, что ковариационная матрица всегда симметрична, поскольку ковариация между двумя переменными не зависит от порядка переменных. Например,
![]()
равно
![]()
Кроме того, ковариационная матрица всегда будет квадратной, а ее размерность будет равна количеству переменных. В этом случае у нас было три переменные, поэтому это матрица 3×3, но если бы у нас было только две переменные, ковариационная матрица была бы 2×2.
Свойства ковариационной матрицы
Ковариационная матрица имеет следующие характеристики:
- Ковариационная матрица представляет собой квадратную матрицу порядка количества переменных.
- Ковариационная матрица симметрична, это означает, что главная диагональ матрицы является осью симметрии.
- Ковариационная матрица всегда положительно полуопределена.
- Определитель ковариационной матрицы равен или больше нуля.