Может ли эксцесс быть отрицательным?

В статистике эксцесс используется для описания формы распределения вероятностей.

В частности, он говорит нам, насколько хорошо значения данных группируются в хвостах или наверху распределения.

Эксцесс распределения может быть отрицательным, нулевым или положительным.

Нулевой эксцесс

Если эксцесс распределения равен 0, то оно равно нормальному распределению, имеющему следующую колоколообразную форму:

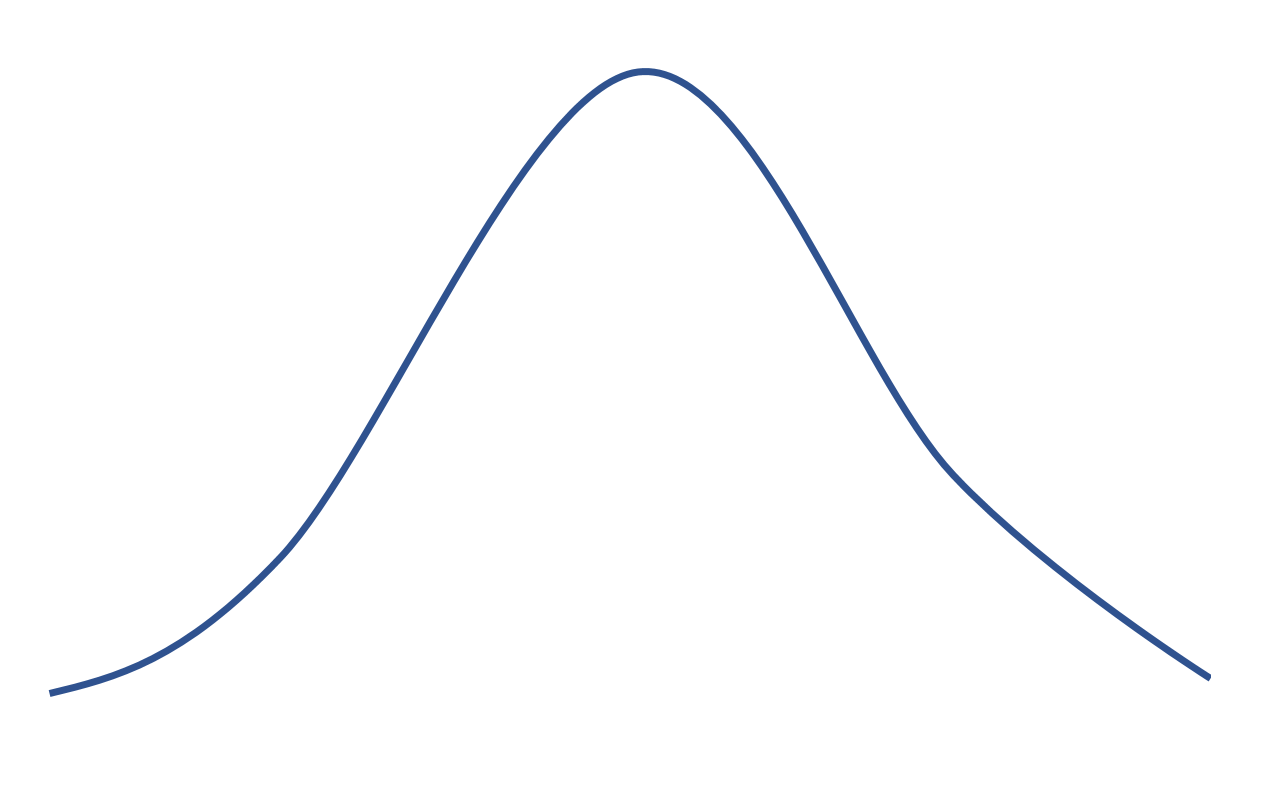
Положительный эксцесс

Если распределение имеет положительный эксцесс, его называют лептокуртическим , то есть оно имеет более острый пик и более тяжелые хвосты по сравнению с нормальным распределением.

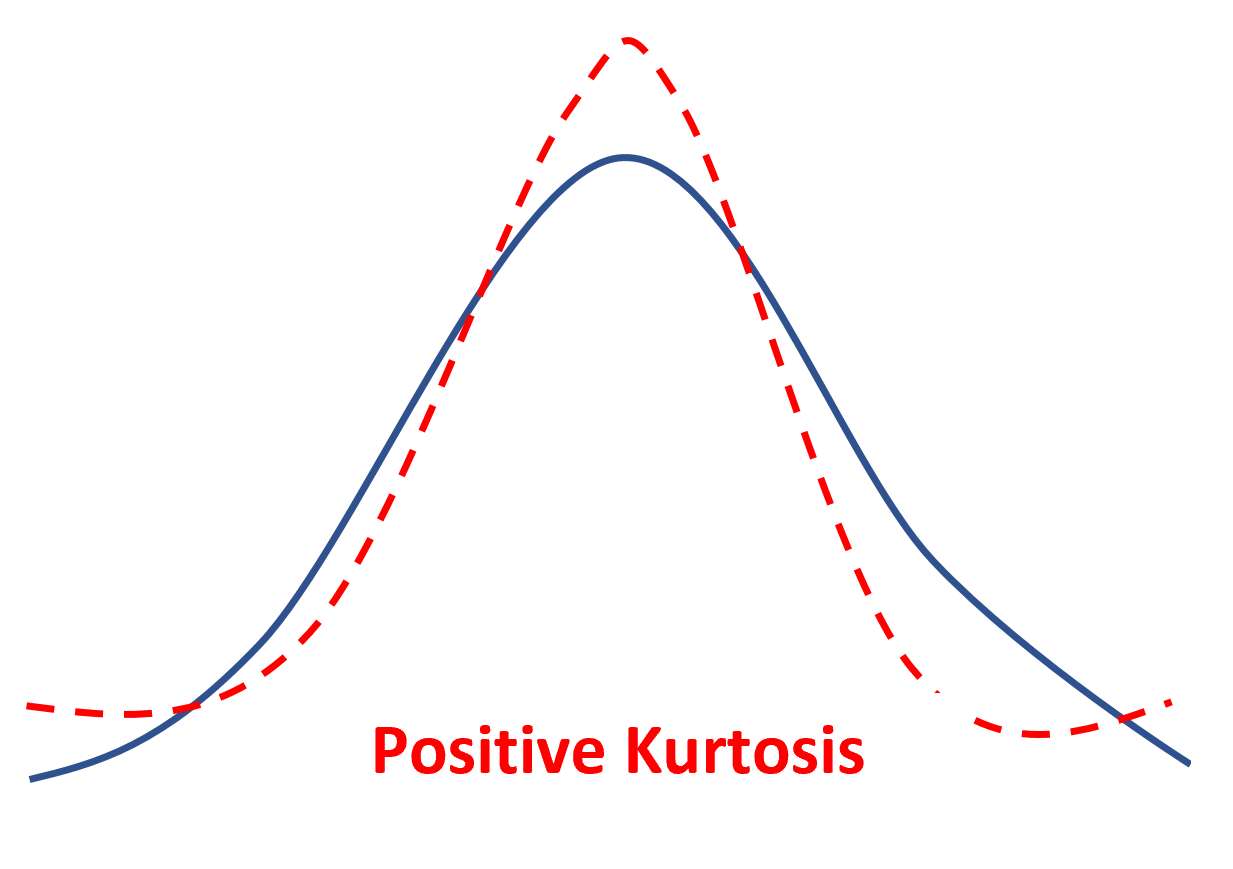
Это просто означает, что меньше значений данных расположено вблизи среднего значения, а больше значений данных расположено на хвостах.

Наиболее известным распределением, имеющим положительный эксцесс, является t-распределение, которое имеет более острый пик и более тяжелые хвосты по сравнению с нормальным распределением.

Отрицательный эксцесс

Если распределение имеет отрицательный эксцесс, оно называется платикуртным , что означает, что оно имеет более плоский пик и более тонкие хвосты по сравнению с нормальным распределением.

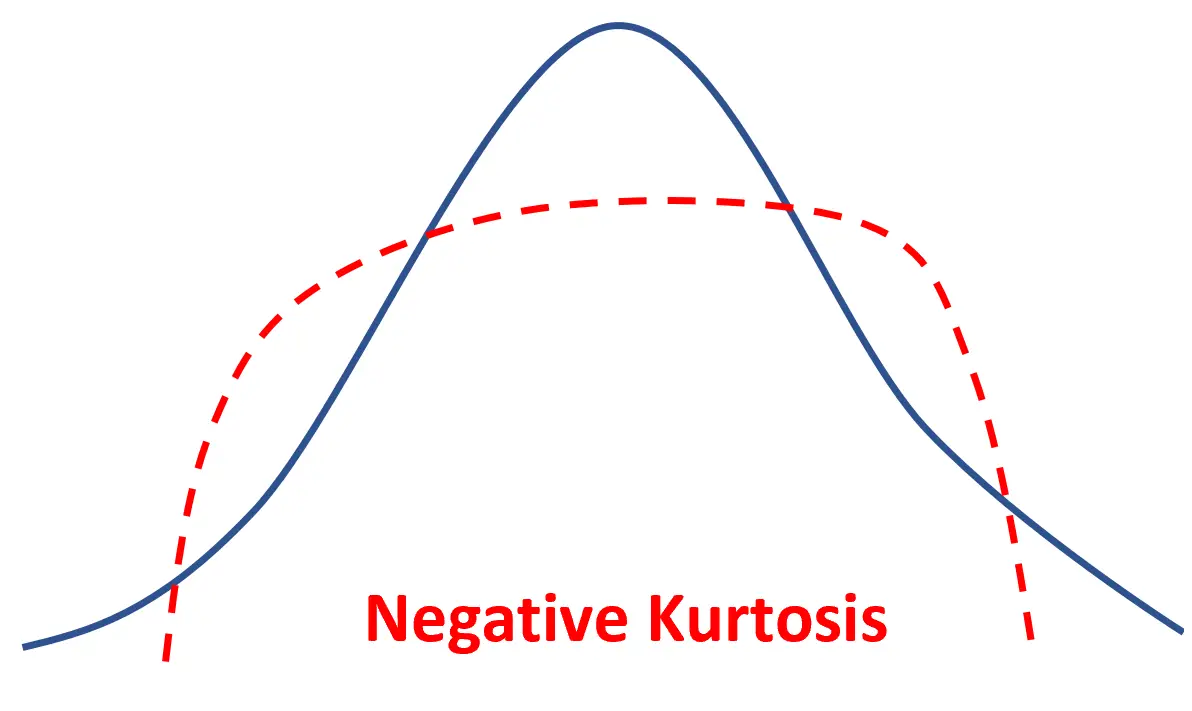
Это просто означает, что больше значений данных расположено вблизи среднего значения и меньше значений данных расположено на хвостах.

Крайним примером распределения, демонстрирующего отрицательный эксцесс, является равномерное распределение , которое не имеет пиков и представляет собой совершенно плоское распределение.

Когда следует использовать лесть на практике

На практике мы часто измеряем эксцесс распределения на исследовательском этапе анализа, когда просто пытаемся лучше понять данные.

Итак, если мы видим, что эксцесс положителен, мы знаем, что работаем с распределением, в котором меньше значений данных расположено рядом с центром и больше значений данных распределено вдоль хвостов.

И наоборот, если мы видим, что эксцесс отрицательный, мы знаем, что работаем с распределением, в котором больше значений данных расположено вблизи центра и меньше значений данных в хвостах.

Дополнительные ресурсы

Чтобы найти асимметрию и эксцесс данного распределения, вы можете ввести значения необработанных данных в этот калькулятор асимметрии и эксцесса , который сообщит вам как асимметрию, так и эксцесс распределения.

Одним из наиболее популярных статистических тестов, используемых для определения того, демонстрирует ли конкретное распределение асимметрию и эксцесс, соответствующий нормальному распределению, является тест Харке Бера .

В Академии Хана также есть хорошая серия видеороликов , в которых описывается, как классифицировать формы распределения.