Независимая переменная

В этой статье объясняется, что такое независимые переменные. Таким образом, вы узнаете значение независимой переменной в математике и статистике, а также увидите несколько примеров этого типа переменных.

Что такое независимая переменная?

Независимая переменная — это переменная, значение которой не зависит от значения какой-либо другой переменной. Напротив, если независимая переменная меняет свое значение, она меняет значение зависимой переменной.

Когда вы рисуете независимую переменную, она обычно обозначается буквой x и располагается на оси x (горизонтальной оси).

Например, продолжительность аренды недвижимости является независимой переменной, влияющей на цену, которую вы платите. Поскольку продолжительность аренды может быть определена, и ее стоимость влияет на переменную, зависящую от цены, поскольку чем дольше используются объекты, тем больше они должны платить.

Независимые переменные также можно назвать объясняющими переменными, входными переменными или управляемыми переменными.

Примеры независимых переменных

Увидев определение независимой переменной, давайте теперь рассмотрим несколько примеров переменных этого типа, чтобы лучше понять концепцию.

• Время, потраченное на обучение (независимая переменная), влияет на полученные оценки (зависимая переменная).
• Цена продукта (независимая переменная) меняет количество людей, желающих купить продукт (зависимая переменная).
• Температура окружающей среды (независимая переменная) влияет на количество лесных пожаров (зависимая переменная).
• Реклама продукта (независимая переменная) влияет на количество продаж этого продукта (зависимая переменная).
• Количество жителей города (независимая переменная) связано с количеством такси в городе (зависимая переменная).

Независимые переменные в математике

В математике причинно-следственная связь обычно моделируется с использованием независимой переменной и зависимой переменной. Таким образом, функция определяет математическую связь, существующую между независимой переменной и зависимой переменной.

Независимые переменные обычно обозначаются буквой x , а буква y используется для обозначения зависимых переменных.

Например, функция y=2x указывает, что когда независимая переменная x увеличивается на одну единицу, зависимая переменная y увеличивается в два раза.

Чтобы узнать больше о математических функциях, мы рекомендуем посетить сайт нашего партнера function.xyz .

Независимые переменные в статистике

Однако в действительности очень сложно найти связь между двумя переменными, которую можно определить с помощью точной математической функции, поскольку иногда одно и то же значение независимой переменной приводит к разным значениям зависимой переменной.

Например, иногда, изучая больше, мы получаем более низкую оценку или, наоборот, изучая меньше, мы получаем более высокую оценку. Поэтому количество часов, которые мы тратим на учебу, — не единственный фактор, влияющий на получаемую оценку, оно также может меняться в зависимости от сложности экзамена или сложности изучаемого предмета.

Поэтому в статистике обычно проводится множество экспериментов, чтобы определить, существует ли связь между независимой переменной и зависимой переменной. Полученные результаты затем можно представить графически, чтобы проверить, связаны ли переменные, и, если да, увидеть, какой тип связи между ними (положительная, отрицательная, линейная, экспоненциальная и т. д.).

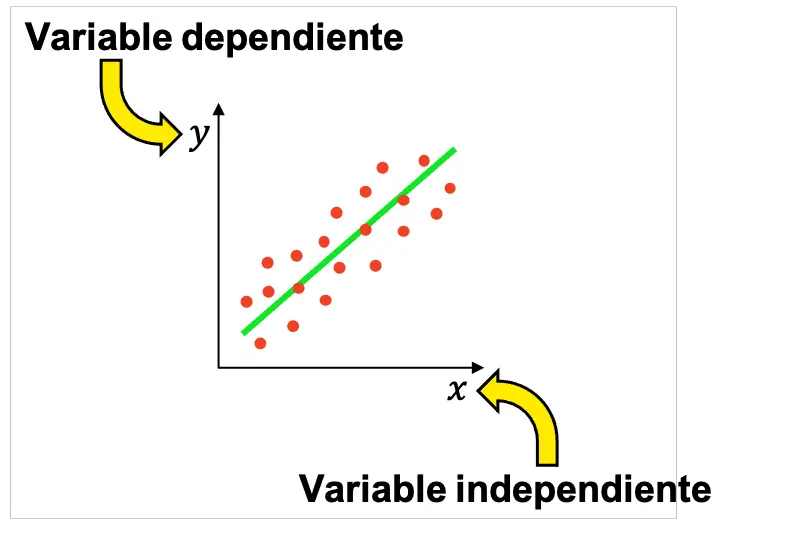
Имейте в виду, что в опросе может быть более одной независимой переменной, хотя самые основные статистические исследования проводятся с одной независимой и одной зависимой переменной.

После проведения статистического исследования можно рассчитать математическую функцию, которая позволит сделать аппроксимацию и, таким образом, смоделировать взаимосвязь между переменными. Обычно сначала вы создаете статистическую модель, а затем математическую модель.