Нормальное распределение и стандартное нормальное распределение: разница

Нормальное распределение является наиболее часто используемым распределением вероятностей в статистике.

Он имеет следующие свойства:

• Симметричный
• Колоколообразный
• Среднее значение и медиана равны; оба расположены в центре распределения

Среднее значение нормального распределения определяет его местоположение, а стандартное отклонение определяет его разброс.

Например, на следующем графике показаны три нормальных распределения с разными средними значениями и стандартными отклонениями:

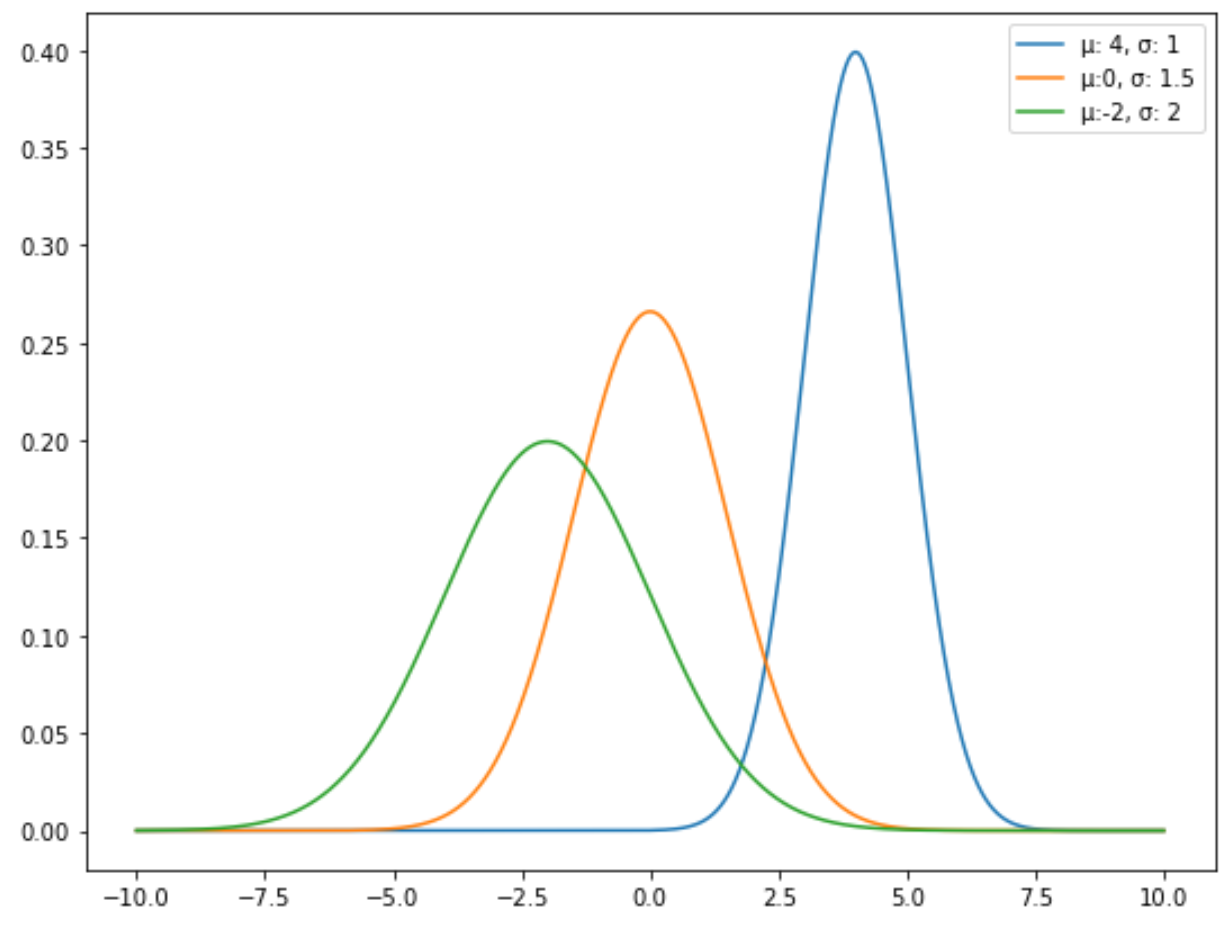
Стандартное нормальное распределение — это особый тип нормального распределения, где среднее значение равно 0, а стандартное отклонение равно 1.

На следующем графике показано стандартное нормальное распределение:

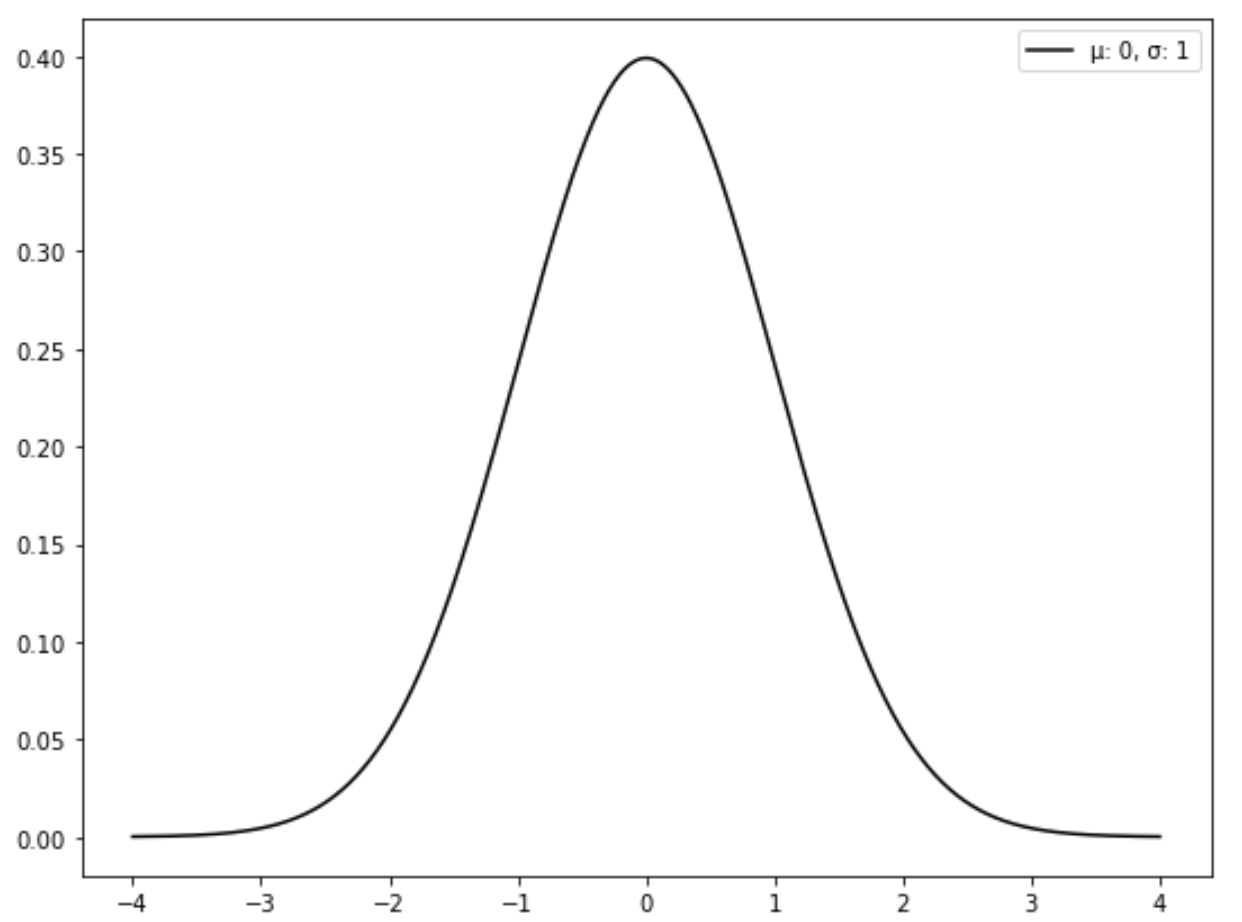
Как преобразовать нормальное распределение в стандартное нормальное распределение

Любое нормальное распределение можно преобразовать в стандартное нормальное распределение путем преобразования значений данных в z-показатели, используя следующую формулу:

z = (x – µ)/σ

Золото:

• x: значение отдельных данных
• μ: среднее значение распределения
• σ: стандартное отклонение распределения.

Например, предположим, что у нас есть следующий набор данных со средним значением 6 и стандартным отклонением 2,152:

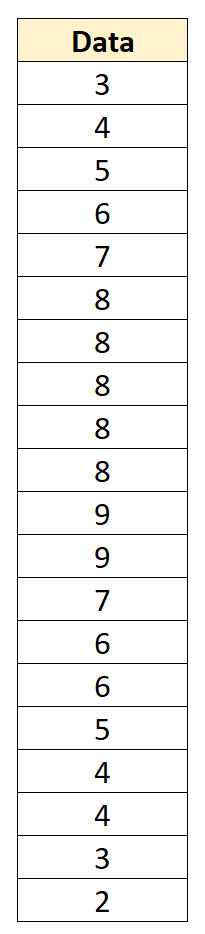
Мы можем преобразовать каждое отдельное значение данных в z-показатель, вычитая 6 из каждого значения и разделяя на 2,152:

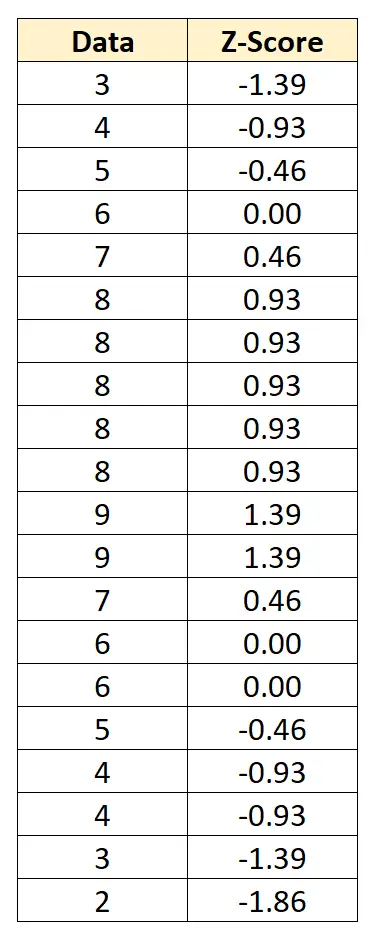
Z-показатель говорит нам, на сколько стандартных отклонений каждая точка данных отличается от среднего значения. Например, первое значение данных «3» на 1,39 стандартных отклонения ниже среднего.

Среднее значение этого распределения оценок имеет среднее значение, равное нулю, и стандартное отклонение, равное единице.

Как использовать стандартное нормальное распределение

Стандартное нормальное распределение обладает следующими свойствами:

• Около 68% данных находятся в пределах одного стандартного отклонения от среднего значения.
• Около 95% данных находятся в пределах двух стандартных отклонений от среднего значения.
• Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.

Это известно как практическое правило и используется для понимания распределения значений в наборе данных.

Например, предположим, что высота растений в определенном саду обычно распределяется со средним значением 47,4 дюйма и стандартным отклонением 2,4 дюйма.

Используя эмпирическое правило, какой процент растений имеет высоту менее 54,6 дюймов?

Эмпирическое правило гласит, что для данного набора данных с нормальным распределением 99,7% значений данных попадают в пределы трех стандартных отклонений от среднего значения. Это означает, что 49,85% значений попадают между средним значением и тремя стандартными отклонениями выше среднего.

В этом примере 54,6 — это на три стандартных отклонения выше среднего значения. Поскольку мы знаем, что 50% значений данных меньше среднего в нормальном распределении, всего 50% + 49,85% = 99,85% значений меньше 54,6.

Таким образом, 99,85% растений имеют высоту менее 54,6 дюймов.

Дополнительные ресурсы

Проблемы с применением эмпирических правил
Правила практического калькулятора
Как применить эмпирическое правило в Excel