Отношение шансов и относительный риск: в чем разница?
Два термина, которые студенты часто путают в статистике, — это отношение шансов и относительный риск .
Мы часто используем эти две метрики при анализе таблицы 2 на 2, которая имеет следующий формат:

Отношение шансов показывает нам соотношение между вероятностью события, произошедшего в экспериментальной группе, и вероятностью события, произошедшего в контрольной группе. Он рассчитывается следующим образом:
Отношение шансов = (A*D) / (B*C)
Относительный риск показывает нам соотношение между вероятностью события, произошедшего в экспериментальной группе, и вероятностью события, произошедшего в контрольной группе. Он рассчитывается следующим образом:
Относительный риск = [A/(A+B)] / [C/(C+D)]
Короче говоря, вот разница:
- Отношение шансов — это соотношение двух шансов .
- Относительный риск представляет собой соотношение двух вероятностей .
В следующем примере показано, как рассчитать и интерпретировать отношение шансов и относительный риск в реальной ситуации.
Пример: расчет отношения шансов и относительного риска
Предположим, что 100 баскетболистов используют новую программу тренировок, а 100 игроков используют старую программу тренировок. В конце программы мы проверяем каждого игрока, чтобы увидеть, прошел ли он определенный тест на навыки.
В следующей таблице показано количество игроков, сдавших и не сдавших экзамен, в зависимости от используемой ими программы:
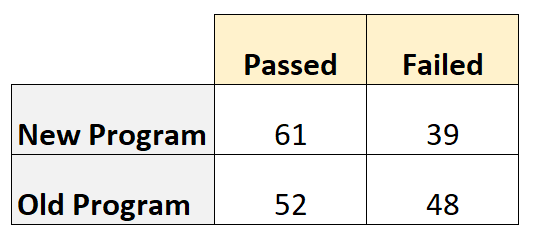
Отношение шансов рассчитывается следующим образом:
- Отношение шансов = (A*D) / (B*C)
- Коэффициент шансов = (61*48) / (39*52)
- Коэффициент шансов = 1,44
Мы бы интерпретировали это так, что шансы игрока пройти тест, используя новую программу , в 1,44 раза превышают шансы игрока пройти тест, используя старую программу.
Другими словами, шансы игрока пройти тест увеличиваются за счет использования новой программы.
Относительный риск рассчитывается как
- Относительный риск = [A/(A+B)] / [C/(C+D)]
- Относительный риск = [61/(61+39)] / [52/(52+48)]
- Относительный риск = 1,17
Мы бы интерпретировали это так, что соотношение между вероятностью прохождения игроком теста с использованием новой программы и старой программы равно 1,17 .
Поскольку это значение больше 1, это говорит нам о том, что вероятность успеха в новой программе выше, чем в старой.
Мы также можем убедиться в этом, непосредственно рассчитав вероятность того, что игрок пройдет по каждой программе:
Вероятность успеха по новой программе = 61/100 = 61%.
Вероятность успеха по старой программе = 52/100 = 52%.
Взяв соотношение этих вероятностей, мы можем рассчитать относительный риск как 61%/52%= 1,17 .
Обратите внимание, что отношение шансов и относительный риск больше 1, что говорит нам о том, что шансы пережить событие (например, пройти тест на навыки) выше в экспериментальной группе, чем в контрольной группе.
Отношение шансов и относительный риск дают нам схожую информацию, но мы интерпретируем каждое значение немного по-разному.
Особенно:
- Отношение шансов говорит нам, что шансы пройти тест на навыки в рамках новой программы выше.
- Относительный риск говорит нам о том, что вероятность прохождения теста на навыки в рамках новой программы выше.
Используя любую метрику, мы легко можем увидеть, что новая программа лучше старой.
Дополнительные ресурсы
Следующие руководства предлагают дополнительную информацию об отношениях шансов и относительном риске:
Как интерпретировать отношения шансов
Как интерпретировать относительный риск
Как рассчитать соотношение шансов и относительный риск в Excel