Отрицательное биномиальное распределение

К бенджамин андерсон 3 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое отрицательное биномиальное распределение и для чего оно используется. Вы также найдете формулу отрицательного биномиального распределения, конкретный пример и свойства этого типа распределения вероятностей. Наконец, вы сможете вычислить любую вероятность отрицательного биномиального распределения с помощью онлайн-калькулятора.

Что такое отрицательное биномиальное распределение?

Отрицательное биномиальное распределение — это распределение вероятностей, которое описывает количество испытаний Бернулли, необходимых для получения заданного количества положительных результатов.

Следовательно, отрицательное биномиальное распределение имеет два характерных параметра: r — количество желаемых успешных результатов и p — вероятность успеха для каждого проведенного эксперимента Бернулли.

$X\sim \text{BN}(r,p)$

Помните, что тест Бернулли — это эксперимент, имеющий два возможных результата: «успех» и «неуспех». Таким образом, если вероятность «успеха» равна p , вероятность «неудачи» равна q=1-p .

Таким образом, отрицательное биномиальное распределение определяет процесс, в котором выполняется столько испытаний Бернулли, сколько необходимо для получения положительных результатов . Более того, все эти испытания Бернулли независимы и имеют постоянную вероятность успеха .

Например, случайная величина, имеющая отрицательное биномиальное распределение, — это количество раз, которое необходимо бросить игральную кость, пока число 6 не будет брошено три раза.

Разница между отрицательным биномиальным распределением и биномиальным распределением заключается в том, что отрицательное биномиальное распределение подсчитывает количество раз, необходимое для получения определенного количества успешных результатов, тогда как биномиальное распределение подсчитывает количество успешных случаев в серии тестов Бернулли.

➤ См.: Что такое биномиальное распределение?

Формула отрицательного биномиального распределения

Учитывая параметры r, p, x, вероятность отрицательного биномиального распределения вычисляется путем умножения комбинаторного числа x-1 в xr на (1-p) ^xr на p ^r .

Итак, формула расчета вероятности отрицательного биномиального распределения :

Формула отрицательного биномиального распределения

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать вероятность переменной, которая соответствует отрицательному биномиальному распределению.

Решенное упражнение отрицательного биномиального распределения

Какова вероятность того, что если подбросить монету восемь раз, то при восьмом броске в четвертый раз выпадет орел?

Во-первых, нам нужно вычислить вероятность выпадения орла при подбрасывании монеты. В этом случае у нас есть только один положительный исход (орёл) из двух возможных исходов (орёл и решка), поэтому вероятность успеха равна:

$p=\cfrac{1}{2}=0,5$

Таким образом, случайная величина в этой задаче имеет отрицательное биномиальное распределение, где r=4 и p=0,5. Поэтому мы используем формулу отрицательного биномиального распределения для расчета вероятности того, что упражнение требует от нас выполнения.

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

Характеристики отрицательного биномиального распределения

Ниже приведены наиболее важные характеристики отрицательного биномиального распределения.

Отрицательное биномиальное распределение определяется двумя характерными параметрами: r — количество желаемых успешных результатов и p — вероятность успеха для каждого проведенного эксперимента Бернулли.

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

Дисперсия отрицательного биномиального распределения равна r , умноженному на (1-p), делённому на p ² .

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

Если параметр r больше 1, режим отрицательного биномиального распределения можно рассчитать по следующей формуле:

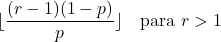
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=»Rendered by QuickLaTeX.com» height=»42″ width=»221″ style=»vertical-align: -16px;»></p> </p> <ul> <li> Функция масс, позволяющая определить вероятность отрицательного биномиального распределения, имеет следующий вид:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

Коэффициент асимметрии отрицательного биномиального распределения рассчитывается по следующему выражению:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

Эксцесс отрицательного биномиального распределения можно найти по следующей формуле:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

Если параметр r равен 1, то мы имеем случай геометрического распределения .

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

Калькулятор отрицательного биномиального распределения

Введите значения параметров r, p, x в следующий калькулятор, чтобы рассчитать вероятность. Вы должны вводить числа, используя точку в качестве десятичного разделителя, например 0,50.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше