Что такое переобучение в машинном обучении? (объяснение и примеры)
В машинном обучении мы часто создаем модели, чтобы можно было делать точные прогнозы относительно определенных явлений.
Например, предположим, что мы хотим создать регрессионную модель , которая использует переменную-предиктор, потраченное на учебу, для прогнозирования оценки ACT по переменной-ответу для старшеклассников.
Чтобы построить эту модель, мы соберем данные о часах, потраченных на обучение, и соответствующий балл ACT для сотен учащихся в определенном школьном округе.
Затем мы будем использовать эти данные для обучения модели, которая сможет делать прогнозы относительно оценки, которую получит данный учащийся, на основе общего количества изученных часов.
Чтобы оценить полезность модели, мы можем измерить, насколько хорошо прогнозы модели соответствуют наблюдаемым данным. Одной из наиболее часто используемых для этого метрик является среднеквадратическая ошибка (MSE), которая рассчитывается следующим образом:
MSE = (1/n)*Σ(y i – f(x i )) 2
Золото:
- n: общее количество наблюдений
- y i : Значение ответа i-го наблюдения.
- f(x i ): прогнозируемое значение ответа i- го наблюдения.
Чем ближе предсказания модели к наблюдениям, тем ниже будет MSE.
Однако одна из самых больших ошибок, допущенных в машинном обучении, — это оптимизация моделей для уменьшения MSE обучения , то есть того, насколько хорошо прогнозы модели соответствуют данным, которые мы использовали для обучения модели.
Когда модель слишком сильно фокусируется на уменьшении MSE обучения, она часто работает слишком усердно, чтобы найти закономерности в обучающих данных, которые просто вызваны случайностью. Затем, когда модель применяется к невидимым данным, ее производительность снижается.
Это явление известно как переобучение . Это происходит, когда мы «подгоняем» модель слишком близко к обучающим данным и, таким образом, в конечном итоге создаем модель, которая бесполезна для прогнозирования новых данных.
Пример переобучения
Чтобы понять переоснащение, давайте вернемся к примеру создания регрессионной модели, которая использует часы, потраченные на обучение , для прогнозирования оценки ACT .
Допустим, мы собираем данные для 100 учащихся в определенном школьном округе и создаем быструю диаграмму рассеяния, чтобы визуализировать взаимосвязь между двумя переменными:
Отношения между двумя переменными кажутся квадратичными, поэтому предположим, что мы применим следующую модель квадратичной регрессии:
Оценка = 60,1 + 5,4*(Часы) – 0,2*(Часы) 2
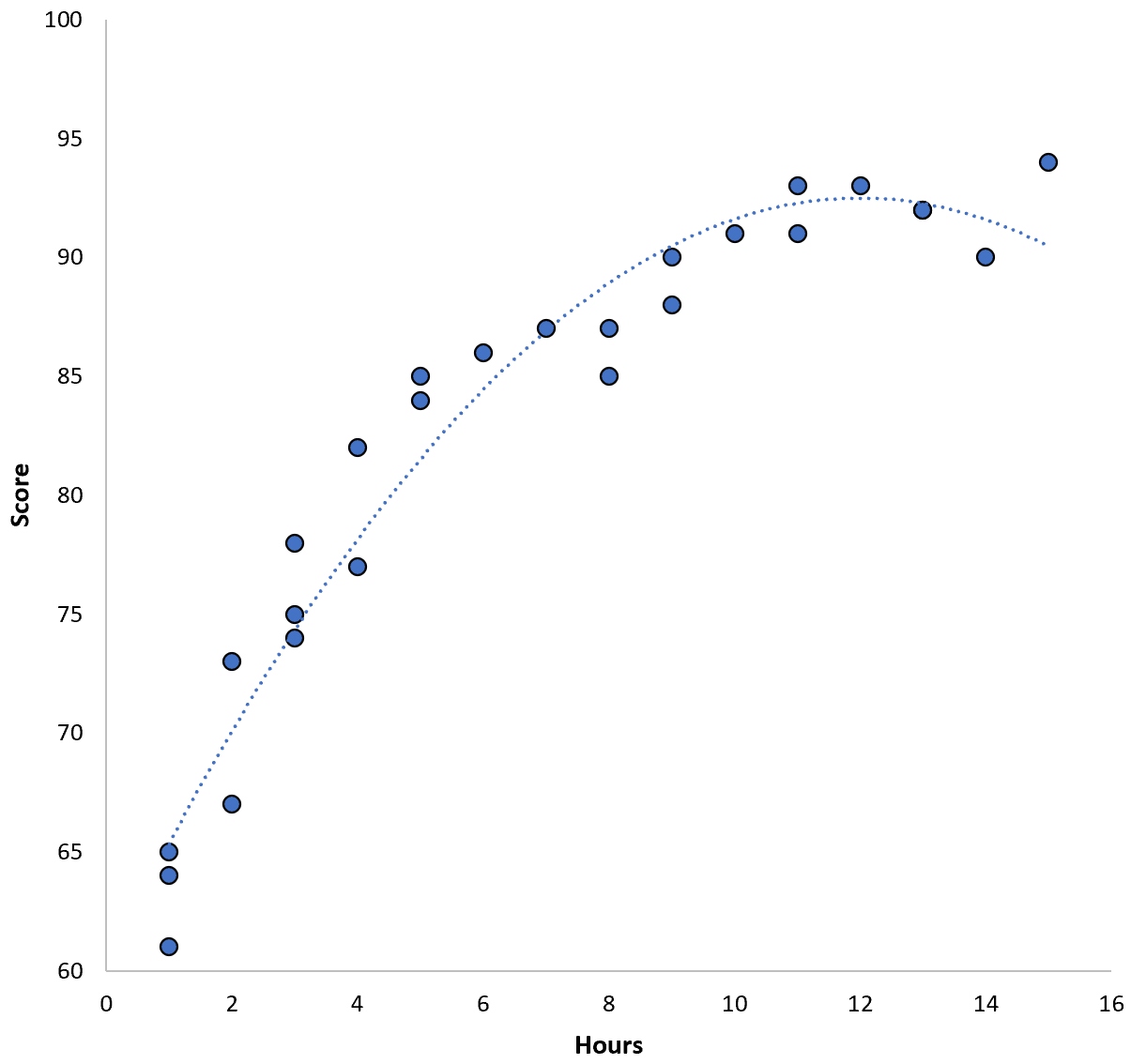
Эта модель имеет среднеквадратическую ошибку обучения (MSE) 3,45 . То есть среднеквадратическая разница между прогнозами, сделанными моделью, и фактическими оценками ACT составляет 3,45.
Однако мы могли бы уменьшить эту обучающую MSE, подобрав полиномиальную модель более высокого порядка. Например, предположим, что мы применяем следующую модель:
Оценка = 64,3 – 7,1*(Часы) + 8,1*(Часы) 2 – 2,1*(Часы) 3 + 0,2*(Часы ) 4 – 0,1*(Часы) 5 + 0,2(Часы) 6
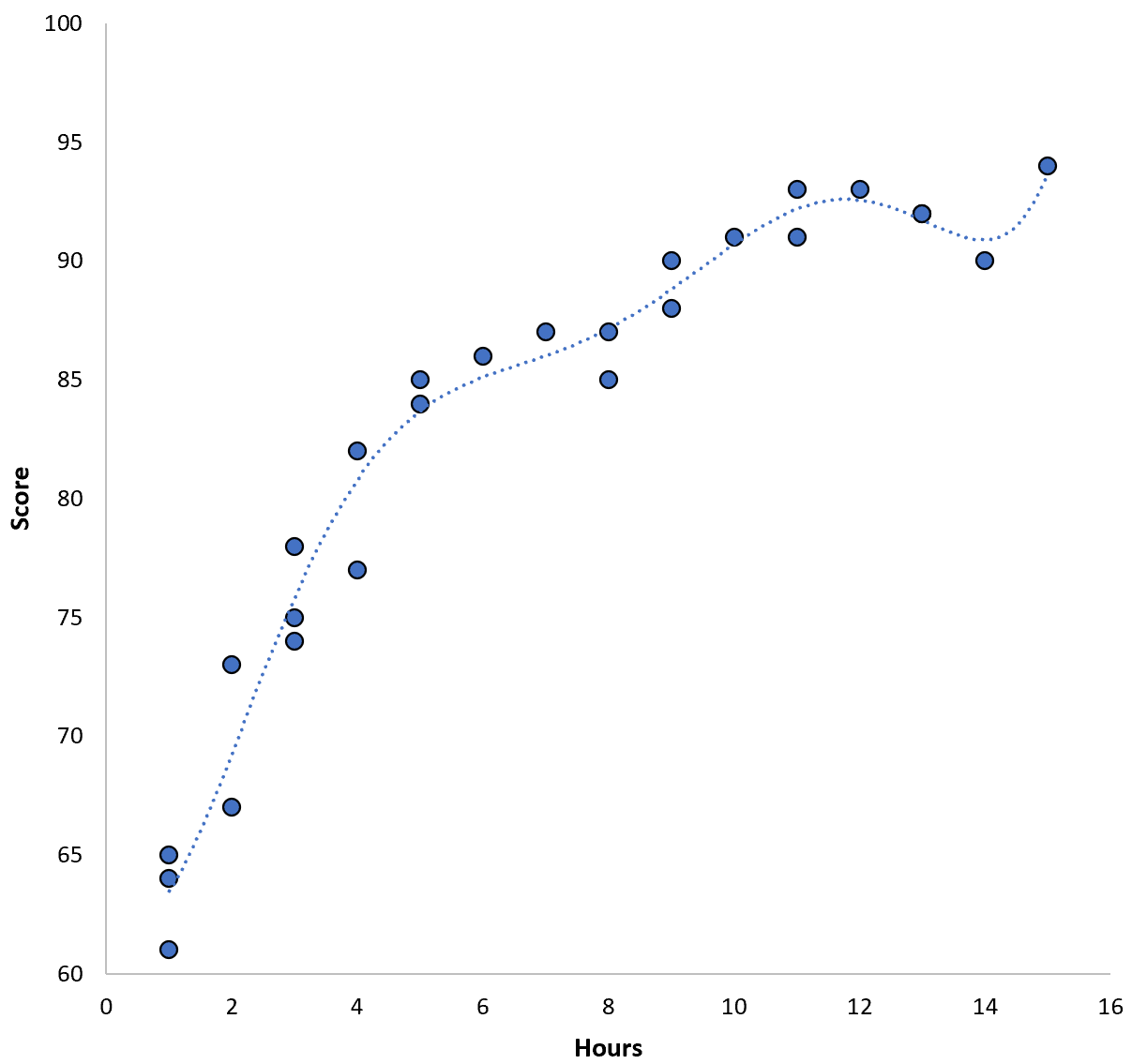
Обратите внимание, что линия регрессии гораздо лучше соответствует фактическим данным, чем предыдущая линия регрессии.
Эта модель имеет среднеквадратическую ошибку обучения (MSE) всего 0,89 . То есть среднеквадратическая разница между прогнозами, сделанными моделью, и фактическими оценками ACT составляет 0,89.
Это обучение MSE намного меньше, чем обучение по предыдущей модели.
Однако нас не особо волнует обучающая MSE , то есть насколько хорошо прогнозы модели соответствуют данным, которые мы использовали для обучения модели. Вместо этого нас в основном волнует тест MSE — MSE, когда наша модель применяется к невидимым данным.
Если бы мы применили описанную выше модель полиномиальной регрессии более высокого порядка к невидимому набору данных, она, вероятно, работала бы хуже, чем более простая модель квадратичной регрессии. То есть это приведет к более высокому результату теста MSE, а это именно то, чего мы не хотим.
Как обнаружить и избежать переобучения
Самый простой способ обнаружить переоснащение — выполнить перекрестную проверку. Наиболее часто используемый метод известен как k-кратная перекрестная проверка и работает следующим образом:
Шаг 1. Случайным образом разделите набор данных на k групп или «складок» примерно одинакового размера.

Шаг 2: Выберите одну из складок в качестве набора для удержания. Подгоните шаблон под оставшиеся k-1 складок. Рассчитайте тест MSE на основе наблюдений в слое, который был натянут.

Шаг 3: Повторите этот процесс k раз, каждый раз используя другой набор в качестве набора исключений.

Шаг 4. Рассчитайте общую MSE теста как среднее из k MSE теста.
Тест MSE = (1/k)*ΣMSE i
Золото:
- k: количество складок
- MSE i : проверить MSE на i-й итерации.
Этот тест MSE дает нам хорошее представление о том, как данная модель будет работать на неизвестных данных.
На практике мы можем подогнать несколько разных моделей и выполнить k-кратную перекрестную проверку каждой модели, чтобы определить ее тест MSE. Затем мы можем выбрать модель с наименьшим тестом MSE как лучшую модель для прогнозирования в будущем.
Это гарантирует, что мы выберем модель, которая, вероятно, будет лучше всего работать с будущими данными, в отличие от модели, которая просто сводит к минимуму обучающую MSE и хорошо «подгоняется» к историческим данным.
Дополнительные ресурсы
Каков компромисс между смещением и дисперсией в машинном обучении?
Введение в перекрестную проверку K-fold
Модели регрессии и классификации в машинном обучении