Что такое полиномиальный тест? (определение & #038; пример)
Полиномиальный тест используется для определения того, соответствует ли категориальная переменная гипотетическому распределению.
В этом тесте используются следующие нулевые и альтернативные гипотезы :
H 0 : Категориальная переменная следует гипотетическому распределению.
H A : Категориальная переменная не соответствует гипотетическому распределению.
Если значение p теста ниже определенного уровня значимости (например, α = 0,05), то мы можем отклонить нулевую гипотезу и сделать вывод, что переменная не соответствует предполагаемому распределению.
Этот тест используется, когда переменная может принимать k разных результатов. Классический пример полиномиального теста — это когда мы хотим определить, являются ли определенные игральные кости честными. Когда вы бросаете игральную кость, вероятность того, что на ней выпадет каждое число (от 1 до 6), равна 1/6.
Чтобы проверить, является ли игральная кость честной, мы можем бросить ее несколько раз и посмотреть, существенно ли отличается количество выпадений на разных числах от ожидаемого.
В следующих примерах показано, как выполнить полиномиальный тест с использованием языка статистического программирования R.
Пример 1: Честные игральные кости
Предположим, мы хотим определить, честна ли кость. Чтобы проверить это, мы запускаем его 30 раз и записываем частоту каждого результата. В следующей таблице показаны результаты:
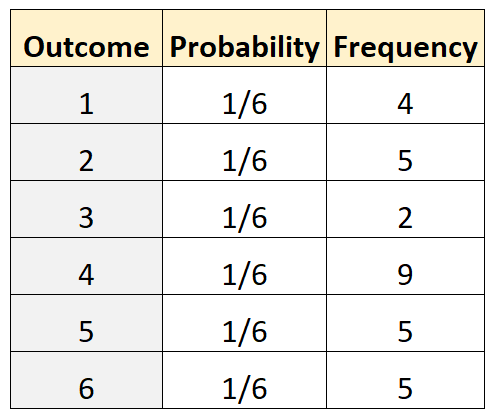
Следующий код на R можно использовать для выполнения полиномиального теста:
library (EMT)
#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)
#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
324632 0 0.4306
P-значение теста составляет 0,4306 . Поскольку это значение p не меньше 0,05, мы не будем отвергать нулевую гипотезу. Таким образом, у нас недостаточно доказательств, чтобы сказать, что кости несправедливы.
Пример 2: Продажа продукции
Предположим, владелец магазина предполагает, что одинаковое количество покупателей купят каждый из четырех разных товаров. Чтобы проверить это, компания записывает количество клиентов, купивших каждый продукт за данную неделю. В следующей таблице показаны результаты:
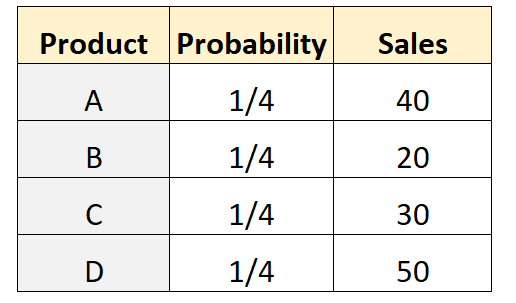
Следующий код на R можно использовать для выполнения полиномиального теста в этом наборе данных:
library (EMT)
#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
477191 0 0.00226
P-значение теста составляет 0,00226 . Поскольку это значение p меньше 0,05, мы отклоним нулевую гипотезу. Итак, у нас есть достаточно доказательств, чтобы сказать, что продажи не одинаковы для каждого продукта.
Пример 3: шарики в мешке
Том утверждает, что вероятность выбрать из мешка красный, зеленый или фиолетовый шарик равна 0,2, 0,5 и 0,3 соответственно. Чтобы проверить это, его друг Майк лезет в сумку и вытаскивает шарик (с запасными частями) 100 раз. В следующей таблице показаны результаты:
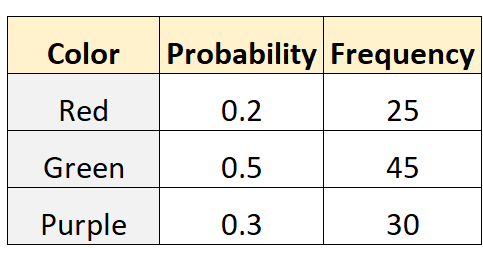
Следующий код на R можно использовать для выполнения полиномиального теста в этом наборе данных:
library (EMT)
#specify probability of each outcome
prob <- c(.2, .5, .3)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
5151 0.0037 0.3999
P-значение теста составляет 0,3999 . Поскольку это значение p не меньше 0,05, мы не сможем отвергнуть нулевую гипотезу. Поэтому у нас нет достаточных доказательств, чтобы сказать, что распределение шариков в мешке отличается от того, которое указал Том.
Дополнительные ресурсы
Введение в полиномиальное распределение
Калькулятор полиномиального распределения