Гипотеза постоянной дисперсии: определение и пример
Линейная регрессия — это метод, который мы используем для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Одним из ключевых предположений линейной регрессии является то, что остатки имеют постоянную дисперсию на каждом уровне предикторной переменной (переменных).
Если это предположение не будет проверено, остатки будут страдать от гетероскедастичности . Когда это происходит, оценки коэффициентов модели становятся ненадежными.
Как оценить постоянную дисперсию
Самый распространенный способ определить, имеют ли остатки регрессионной модели постоянную дисперсию, — это построить график сопоставления подобранных значений с остатками .
Это тип графика, который отображает подобранные значения модели регрессии по оси X и остатки этих значений, расположенные по оси Y.
Если распределение остатков примерно одинаково на каждом уровне подобранных значений, мы говорим, что предположение о постоянной дисперсии удовлетворено.
В противном случае, если дисперсия остатков систематически увеличивается или уменьшается, это предположение, скорее всего, нарушается.
Примечание . График этого типа можно создать только после подгонки модели регрессии к набору данных.
На следующей диаграмме показан пример графика подобранных значений в зависимости от остатков, который отображает постоянную дисперсию :
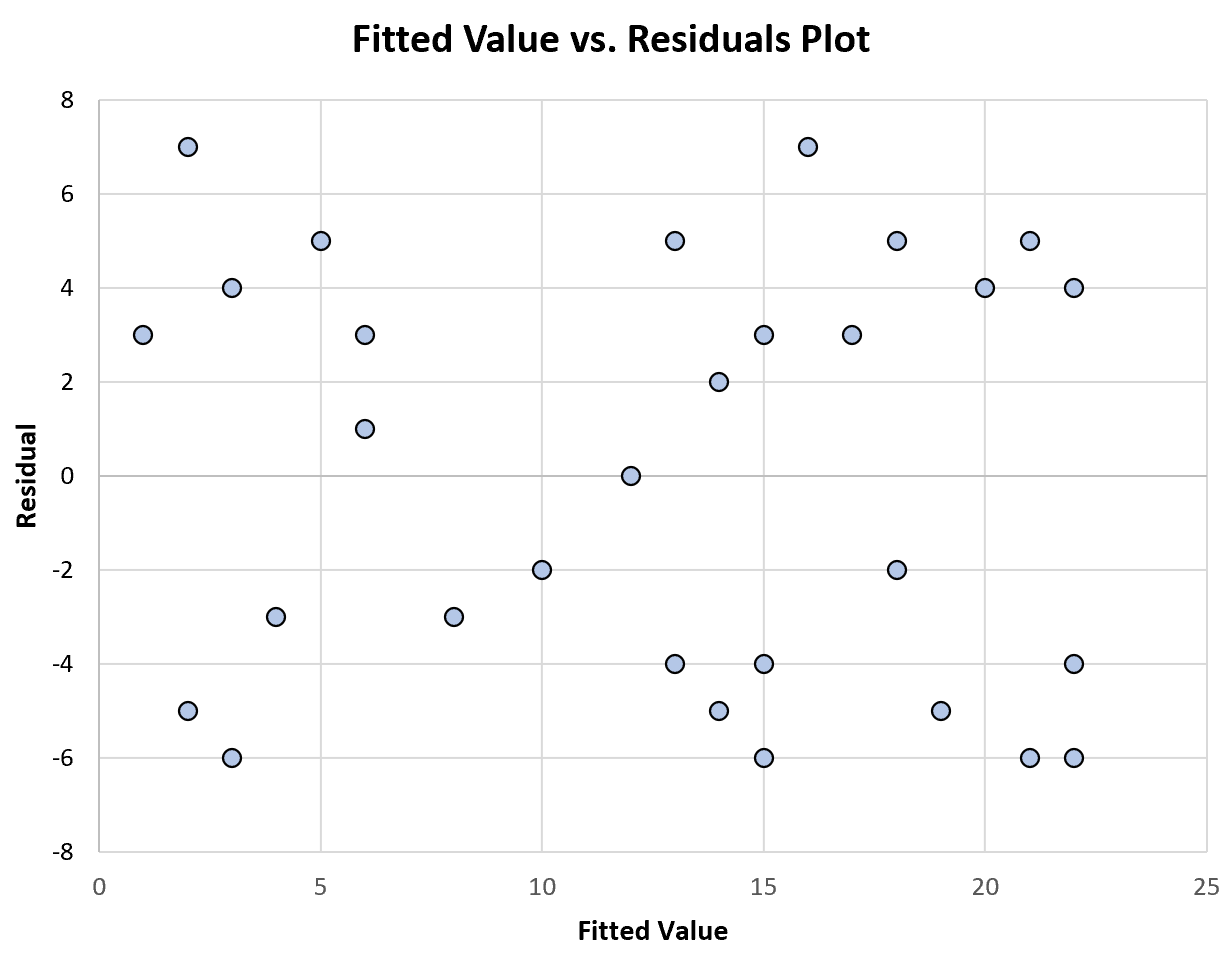
Обратите внимание, как остатки случайным образом разбросаны вокруг нуля, без какой-либо конкретной закономерности, с примерно постоянной дисперсией на каждом уровне подобранных значений.
На следующей диаграмме показан пример графика подобранных значений в зависимости от остатков, который отображает непостоянную дисперсию :
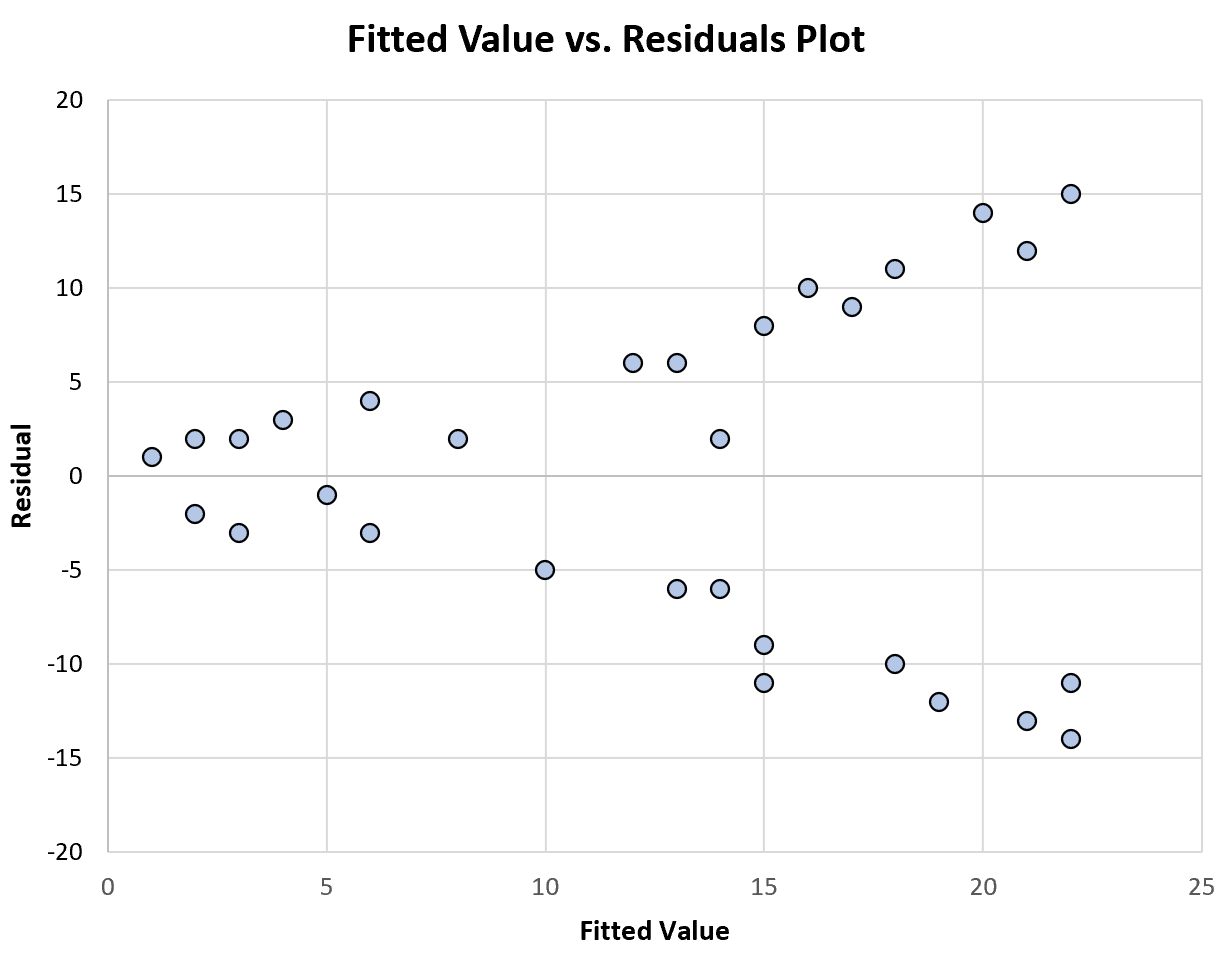
Обратите внимание, что распределение остатков становится больше по мере увеличения подобранных значений. Это типичный признак непостоянной дисперсии.
Это говорит нам о том, что наша регрессионная модель страдает от непостоянной дисперсии остатков и, следовательно, оценки коэффициентов модели ненадежны.
Как исправить нарушение постоянной дисперсии
Если предположение о постоянной дисперсии нарушается, наиболее распространенным способом решения этой проблемы является преобразование переменной отклика с помощью одного из трех преобразований:
1. Преобразование журнала: преобразуйте переменную ответа из y в log(y).
2. Преобразование квадратного корня: преобразуйте переменную отклика из y в √y.
3. Преобразование корня куба: преобразуйте переменную ответа из y в y 1/3.
Выполняя эти преобразования, проблема непостоянной дисперсии обычно исчезает.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о линейной регрессии и анализе остатков:
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Четыре предположения линейной регрессии
Что такое остатки в статистике?