Как выполнить преобразование бокса-кокса в python

Преобразование Бокса-Кокса — это широко используемый метод преобразования набора данных с ненормальным распределением в набор с более нормальным распределением .

Основная идея этого метода состоит в том, чтобы найти значение λ, при котором преобразованные данные будут максимально близки к нормальному распределению, используя следующую формулу:

• y(λ) = (y ^λ – 1) / λ, если y ≠ 0
• y(λ) = log(y), если y = 0

Мы можем выполнить преобразование Box-Cox в Python, используя функцию scipy.stats.boxcox() .

В следующем примере показано, как использовать эту функцию на практике.

Пример: преобразование Бокса-Кокса в Python

Предположим, мы генерируем случайный набор из 1000 значений из экспоненциального распределения :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

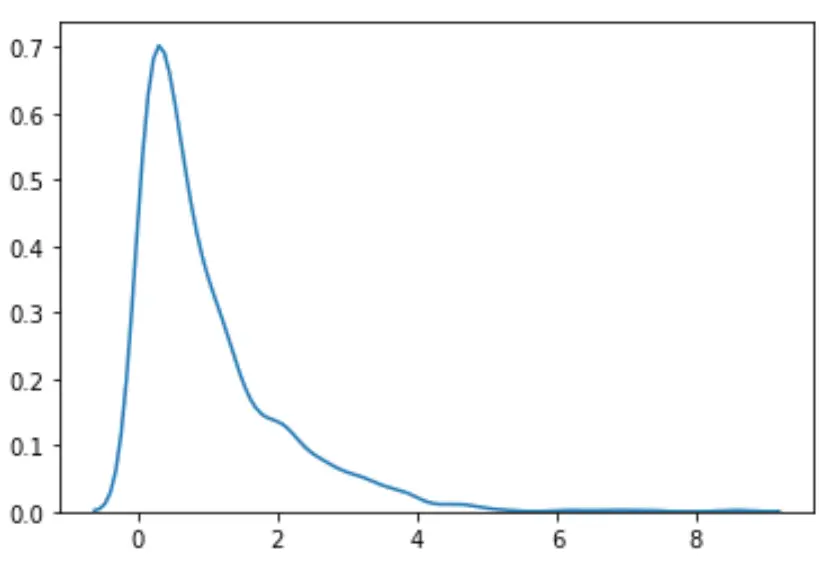
Мы видим, что распределение не кажется нормальным.

Мы можем использовать функцию boxcox() , чтобы найти оптимальное значение лямбды, которое дает более нормальное распределение:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

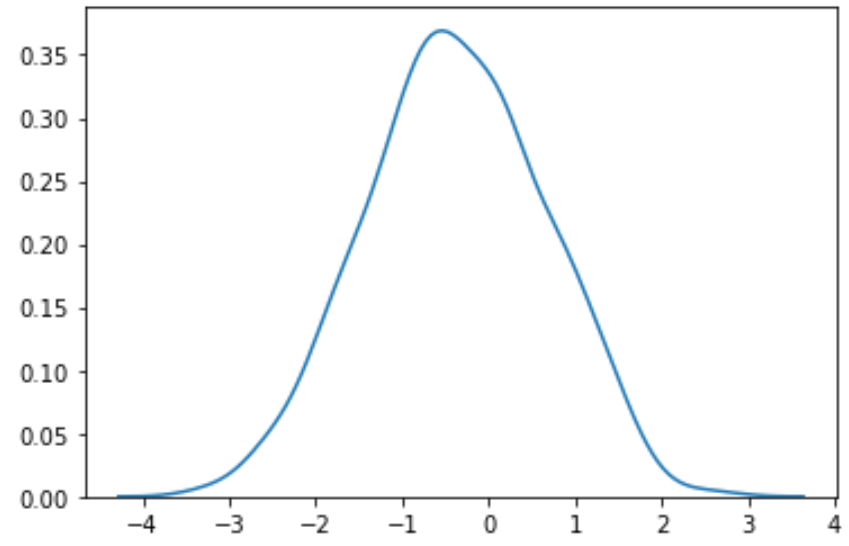
Мы видим, что преобразованные данные имеют гораздо более нормальное распределение.

Мы также можем найти точное значение лямбды, используемое для выполнения преобразования Бокса-Кокса:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

Оптимальная лямбда оказалась около 0,242 .

Таким образом, каждое значение данных было преобразовано с использованием следующего уравнения:

Новое = (старое ^0,242 – 1) / 0,242

Мы можем подтвердить это, сравнивая значения исходных данных и преобразованных данных:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

Первое значение в исходном наборе данных было 0,79587 . Итак, мы применили следующую формулу для преобразования этого значения:

Новый = (0,79587 ^0,242 – 1) / 0,242 = -0,222

Мы можем подтвердить, что первое значение в преобразованном наборе данных действительно равно -0,222 .

Дополнительные ресурсы

Как создать и интерпретировать график QQ в Python
Как выполнить тест на нормальность Шапиро-Уилка в Python