Как преобразовать данные в r (логарифм, квадратный корень, кубический корень)
Многие статистические тесты предполагают, что остатки переменной отклика имеют нормальное распределение.
Однако остатки часто не распределяются нормально. Один из способов решения этой проблемы — преобразовать переменную ответа с помощью одного из трех преобразований:
1. Преобразование журнала: преобразуйте переменную ответа из y в log(y) .
2. Преобразование квадратного корня: преобразуйте переменную ответа из y в √y .
3. Преобразование корня куба: преобразуйте переменную ответа из y в y 1/3 .
Выполняя эти преобразования, переменная ответа обычно приближается к нормальному распределению. Следующие примеры показывают, как выполнить эти преобразования в R.
Преобразование журнала в R
Следующий код показывает, как выполнить преобразование журнала для переменной ответа:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform log transformation log_y <- log10(df$y)
Следующий код показывает, как создавать гистограммы для отображения распределения y до и после выполнения логарифмического преобразования:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for log-transformed distribution hist(log_y, col='coral2', main='Log Transformed')
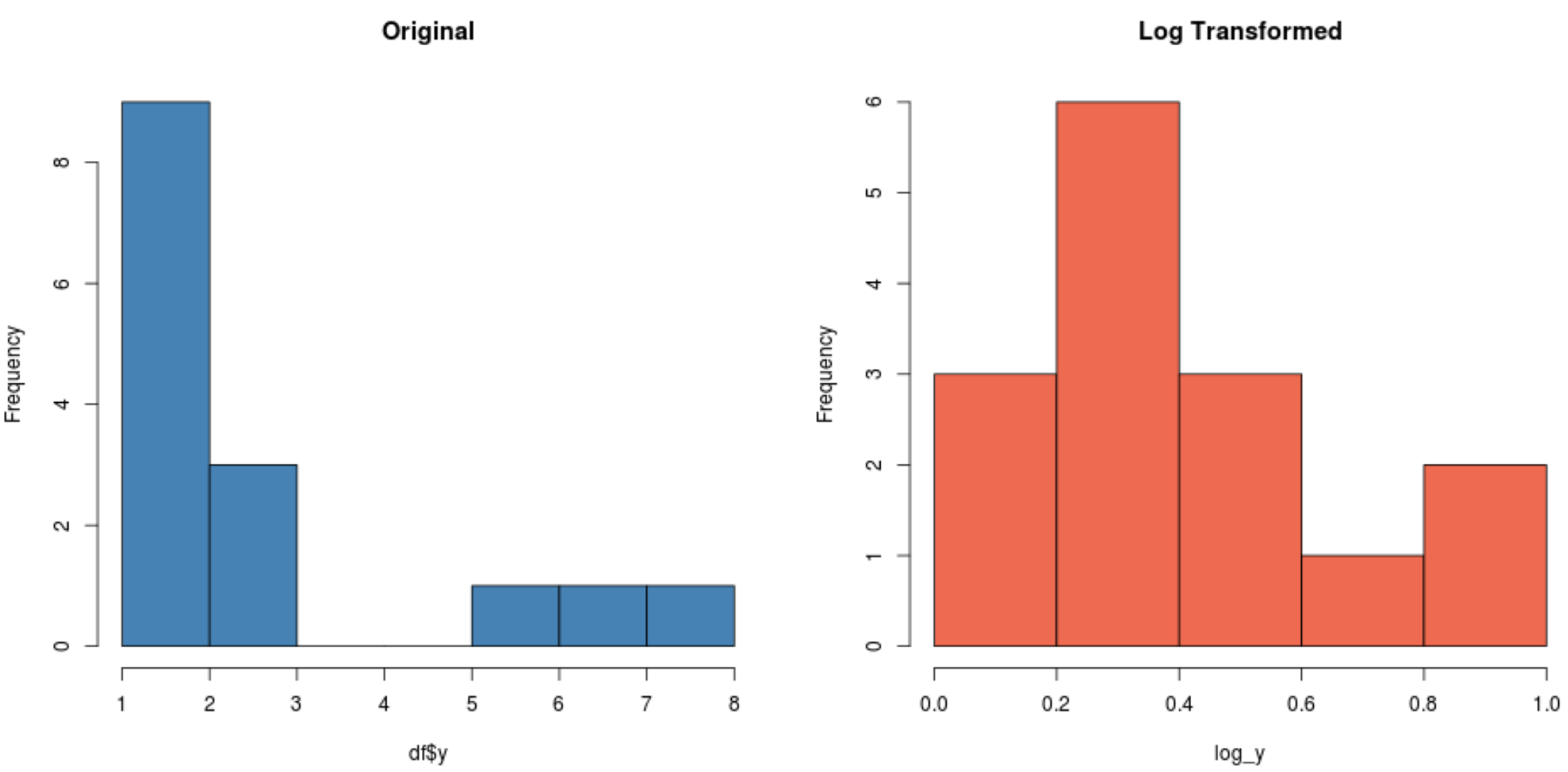
Обратите внимание, что распределение с логарифмическим преобразованием гораздо более нормальное, чем исходное распределение. Это все еще не идеальная «форма колокола», но она ближе к нормальному распределению, чем к исходному распределению.
Фактически, если мы выполним тест Шапиро-Уилка для каждого распределения, мы обнаружим, что исходное распределение не соответствует предположению о нормальности, а логарифмически преобразованное распределение — нет (при α = 0,05):
#perform Shapiro-Wilk Test on original data shapiro.test(df$y) Shapiro-Wilk normality test data: df$y W = 0.77225, p-value = 0.001655 #perform Shapiro-Wilk Test on log-transformed data shapiro.test(log_y) Shapiro-Wilk normality test data:log_y W = 0.89089, p-value = 0.06917
Преобразование квадратного корня в R
Следующий код показывает, как выполнить преобразование квадратного корня для переменной ответа:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation sqrt_y <- sqrt(df$y)
Следующий код показывает, как создавать гистограммы для отображения распределения y до и после выполнения преобразования квадратного корня:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(sqrt_y, col='coral2', main='Square Root Transformed')
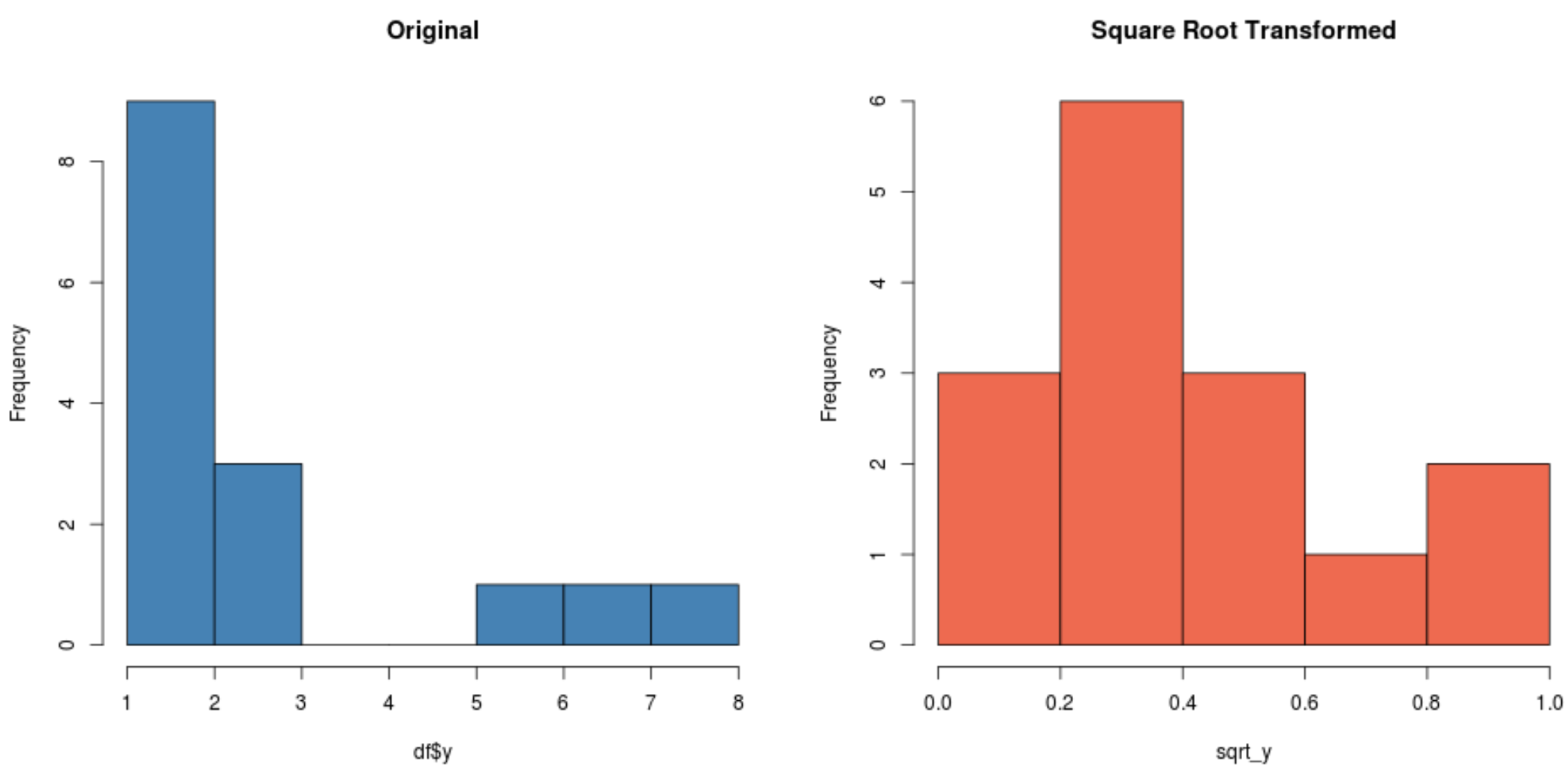
Обратите внимание, что распределение, преобразованное квадратным корнем, распределяется гораздо более нормально, чем исходное распределение.
Преобразование кубического корня в R
Следующий код показывает, как выполнить преобразование кубического корня для переменной ответа:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation cube_y <- df$y^(1/3)
Следующий код показывает, как создавать гистограммы для отображения распределения y до и после выполнения преобразования квадратного корня:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(cube_y, col='coral2', main='Cube Root Transformed')
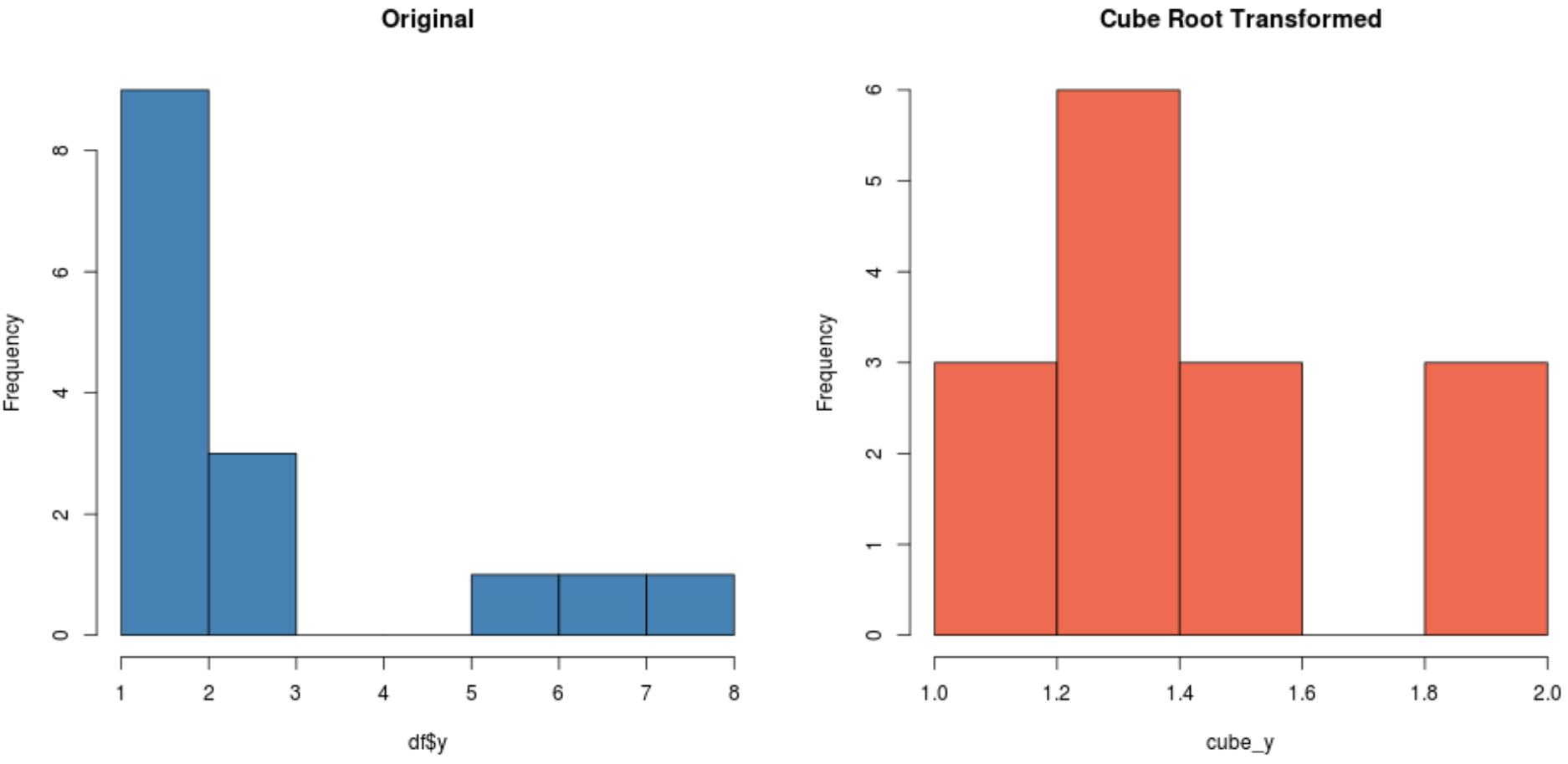
В зависимости от вашего набора данных одно из этих преобразований может создать новый набор данных, который распределяется более нормально, чем другие.