Проверка гипотез на разницу в средних значениях

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое проверка гипотез о разнице средних в статистике и для чего она используется. Кроме того, вы узнаете, как выполнить проверку гипотезы о разнице средних значений, а также пошаговое решение упражнения.

Что такое проверка гипотезы на предмет разницы средних?

Проверка гипотезы на предмет различия средних значений — это статистический тест, используемый для отклонения или принятия гипотезы о том, что средние значения двух популяций различны. То есть проверка гипотезы о разнице средних значений используется для определения того, являются ли средние значения двух популяций одинаковыми или разными.

Имейте в виду, что решения, принимаемые при проверке гипотез, основаны на заранее установленном уровне уверенности , поэтому нельзя гарантировать, что результат проверки гипотезы всегда верен, а скорее, что это наиболее вероятный результат, который является верным.

Проверка гипотезы на разницу двух средних значений включает в себя расчет тестовой статистики и сравнение ее с критическим значением, позволяющим отвергнуть нулевую гипотезу или нет. Ниже мы увидим, как выполнить проверку гипотезы на предмет разницы в средних значениях.

Наконец, помните, что в статистике проверку гипотез можно также назвать контрастом гипотез, проверкой гипотез или проверкой значимости.

➤ См.: Выборочное распределение разницы средних значений.

Формула проверки гипотез на предмет разницы в средних значениях

Формула, которую следует использовать для проверки гипотез о разнице средних значений, варьируется в зависимости от того, известны ли дисперсии генеральной совокупности, а если нет, то можно ли считать их одинаковыми или разными. Итак, в этом разделе мы увидим, какую формулу использовать в зависимости от случая.

Известные варианты

Формула для расчета статистики проверки гипотезы для разницы средних значений, когда дисперсии известны, выглядит следующим образом:

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Золото:

$Z$

— это статистика проверки гипотезы для разницы двух средних значений с известной дисперсией, которая соответствует стандартному нормальному распределению.
$\mu_1$

является средним значением численности населения 1.
$\mu_2$

является средним значением численности населения 2.
$\overline{x_1}$

является средним значением образца 1.
$\overline{x_2}$

является средним значением образца 2.
$\sigma_1$

— стандартное отклонение генеральной совокупности 1.
$\sigma_2$

— стандартное отклонение генеральной совокупности 2.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

Имейте в виду, что это наименее распространенный случай, поэтому эта формула используется только в некоторых конкретных случаях.

Неизвестные и равные отклонения

Формула для расчета статистики проверки гипотезы для разницы средних значений, когда дисперсии генеральной совокупности неизвестны, но считаются равными :

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Золото:

$t$

— это статистика проверки гипотезы для разницы средних значений с неизвестными дисперсиями, которая соответствует t-распределению Стьюдента с n ₁ + n ₂ -2 степенями свободы.
$\mu_1$

является средним значением численности населения 1.
$\mu_2$

является средним значением численности населения 2.
$\overline{x_1}$

является средним значением образца 1.
$\overline{x_2}$

является средним значением образца 2.
$s_p$

представляет собой комбинированное стандартное отклонение.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

Объединенное стандартное отклонение двух выборок рассчитывается по следующей формуле:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Неизвестные и разные вариации

Когда популяционные дисперсии неизвестны и, более того, предполагается, что они различны, формула расчета статистики проверки гипотезы для разницы средних выглядит следующим образом:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Золото:

$t$

— это статистика проверки гипотезы для разницы средних значений с неизвестными дисперсиями, которая соответствует t-распределению Стьюдента.
$\mu_1$

является средним значением численности населения 1.
$\mu_2$

является средним значением численности населения 2.
$\overline{x_1}$

является средним значением образца 1.
$\overline{x_2}$

является средним значением образца 2.
$\sigma_1$

— стандартное отклонение генеральной совокупности 1.
$\sigma_2$

— стандартное отклонение генеральной совокупности 2.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

Однако в этом случае степени свободы t-распределения Стьюдента рассчитываются по следующей формуле:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ См.: Формула доверительного интервала для разницы средних.

Конкретный пример проверки гипотезы о разнице средних значений

Чтобы завершить усвоение концепции проверки гипотез на разнице средних, мы рассмотрим конкретный пример этого типа проверки гипотез.

Вы хотите провести статистическое исследование заработной платы двух конкурирующих компаний, точнее, вы хотите определить, отличается ли средняя зарплата в двух компаниях. Для этого берется выборка из 47 работников одной компании и еще одна выборка из 55 работников другой компании. Средняя зарплата в размере 40 000 долларов США и стандартное отклонение 12 000 долларов США получены из первой выборки, а средняя зарплата в размере 46 000 долларов США и стандартное отклонение 18 000 долларов США получены из второй выборки. Выполните проверку гипотезы с уровнем значимости 5%, чтобы определить, различаются ли средние зарплаты или нет.

В этом случае нулевая гипотеза и альтернативная гипотеза проверки гипотезы на разницу двух средних значений выглядят следующим образом:

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

В этом случае различия в численности населения неизвестны, но можно предположить, что они равны, поскольку это конкурирующие компании и условия работы на рынке, на котором они работают, очень схожи. Следовательно, формула для статистики проверки гипотез для разницы в средних значениях, которую нам следует использовать, выглядит следующим образом:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Поэтому мы рассчитываем объединенное стандартное отклонение двух выборок:

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

Теперь применим формулу проверки гипотезы для разницы средних:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

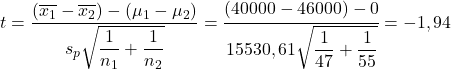
С другой стороны, мы ищем критическое значение проверки гипотезы для разницы в средних значениях в таблице Стьюдента :

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

Затем, поскольку абсолютное значение статистики теста меньше критического значения теста, нулевая гипотеза принимается, а альтернативная гипотеза отклоняется.

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое проверка гипотезы на предмет разницы средних?

Формула проверки гипотез на предмет разницы в средних значениях

Известные варианты

Неизвестные и равные отклонения

Неизвестные и разные вариации

Конкретный пример проверки гипотезы о разнице средних значений

Об авторе

бенджамин андерсон

Добавить комментарий