Как выполнить простую линейную регрессию в excel
Простая линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между объясняющей переменной x и переменной отклика y.
В этом руководстве объясняется, как выполнить простую линейную регрессию в Excel.
Пример: простая линейная регрессия в Excel
Предположим, мы хотим понять взаимосвязь между количеством часов, в течение которых студент готовится к экзамену, и оценкой, которую он получает на экзамене.
Чтобы изучить эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя часы обучения в качестве объясняющей переменной и результаты экзаменов в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы выполнить простую линейную регрессию.
Шаг 1: Введите данные.
Введите следующие данные о количестве учебных часов и результатах экзамена, полученных для 20 студентов:
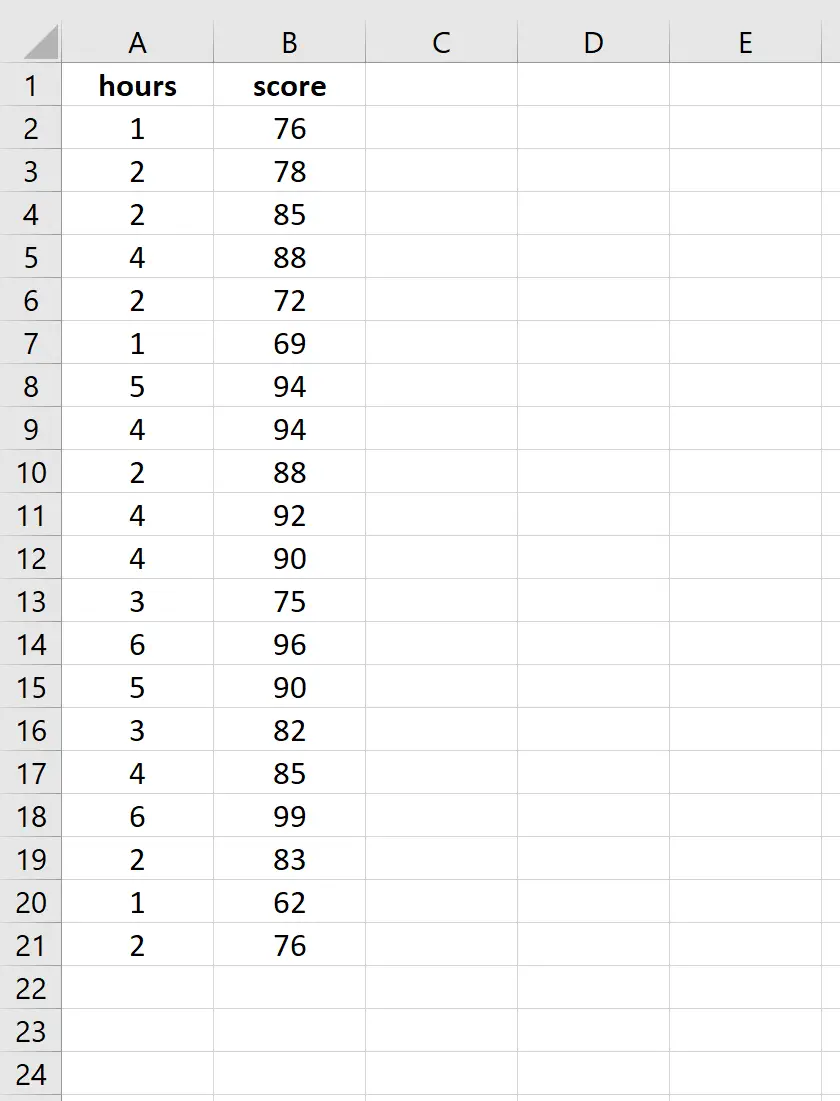
Шаг 2: Визуализируйте данные.
Прежде чем выполнять простую линейную регрессию, полезно создать диаграмму рассеяния данных, чтобы убедиться, что между учебными часами и баллами на экзамене действительно существует линейная связь.
Выделите данные в столбцах A и B. На верхней ленте Excel перейдите на вкладку «Вставка» . В группе «Графика» нажмите «Вставить Scatter (X, Y)» и выберите первый вариант с надписью «Scatter» . Это автоматически создаст следующее облако точек:
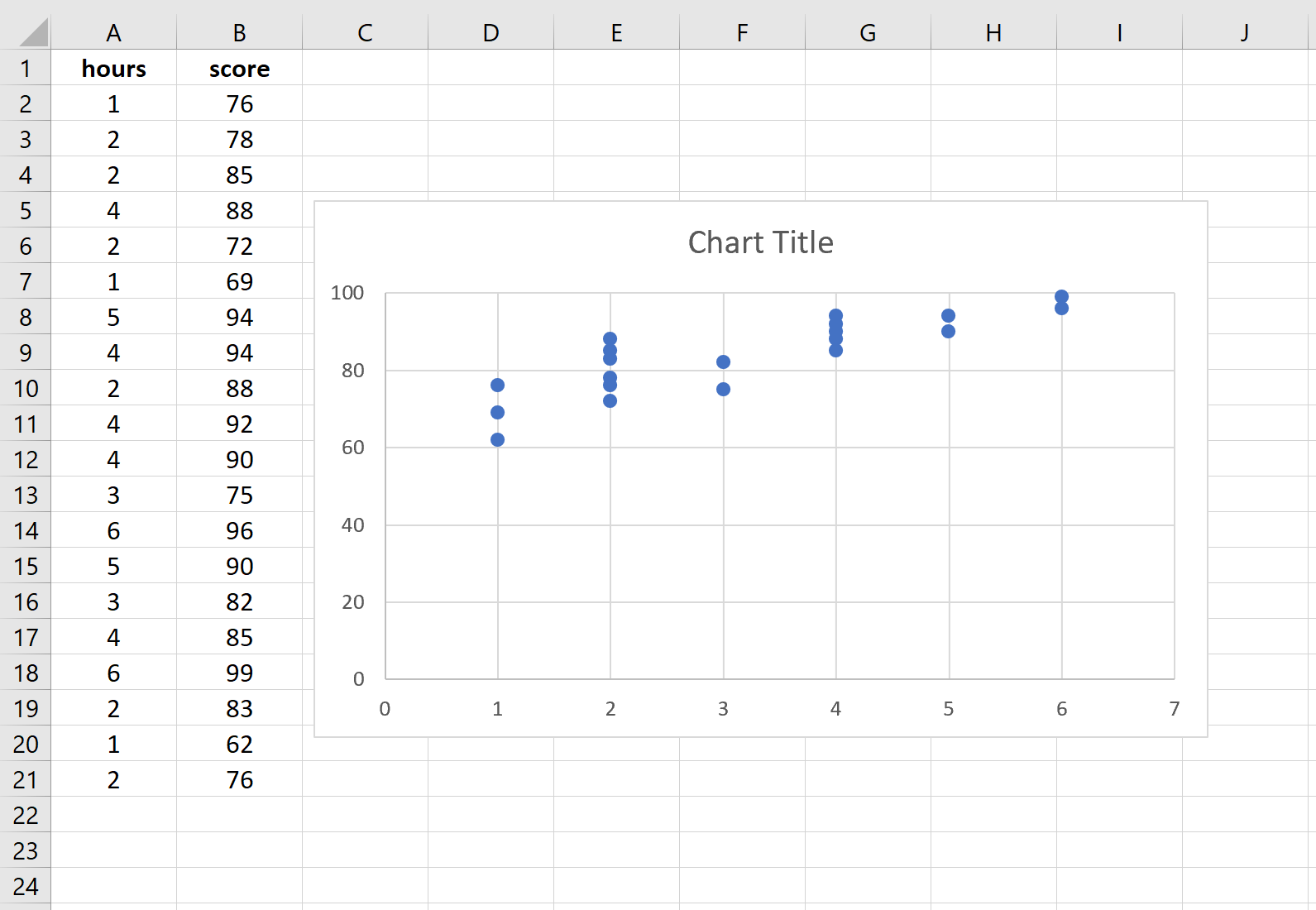
Количество учебных часов показано на оси X, а результаты экзаменов — на оси Y. Мы видим, что между этими двумя переменными существует линейная зависимость: большее количество часов обучения связано с более высокими оценками на экзаменах.
Чтобы количественно оценить связь между этими двумя переменными, мы можем выполнить простую линейную регрессию.
Шаг 3: Выполните простую линейную регрессию.
На верхней ленте Excel перейдите на вкладку «Данные» и нажмите «Анализ данных» . Если вы не видите эту опцию, вам необходимо сначала установить бесплатное программное обеспечение Analysis ToolPak .

После того, как вы нажмете «Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
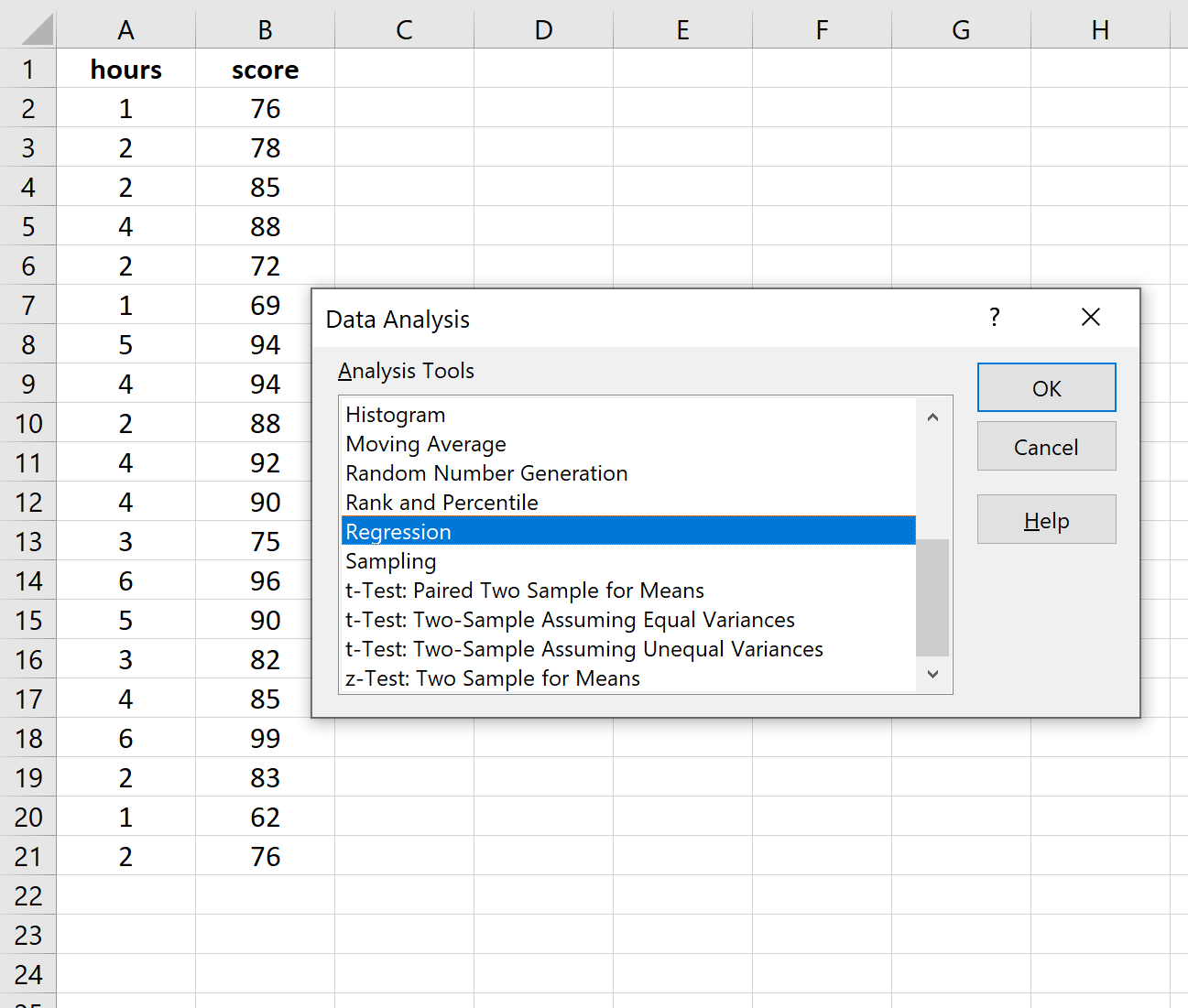
В поле «Входной диапазон Y» заполните массив значений переменной ответа. Для Input X Range заполните массив значений независимой переменной.
Установите флажок рядом с надписью «Метки» , чтобы сообщить Excel, что мы включили имена переменных во входные диапазоны.
В поле Выходной диапазон выберите ячейку, в которой вы хотите, чтобы отображались выходные данные регрессии.
Затем нажмите ОК .
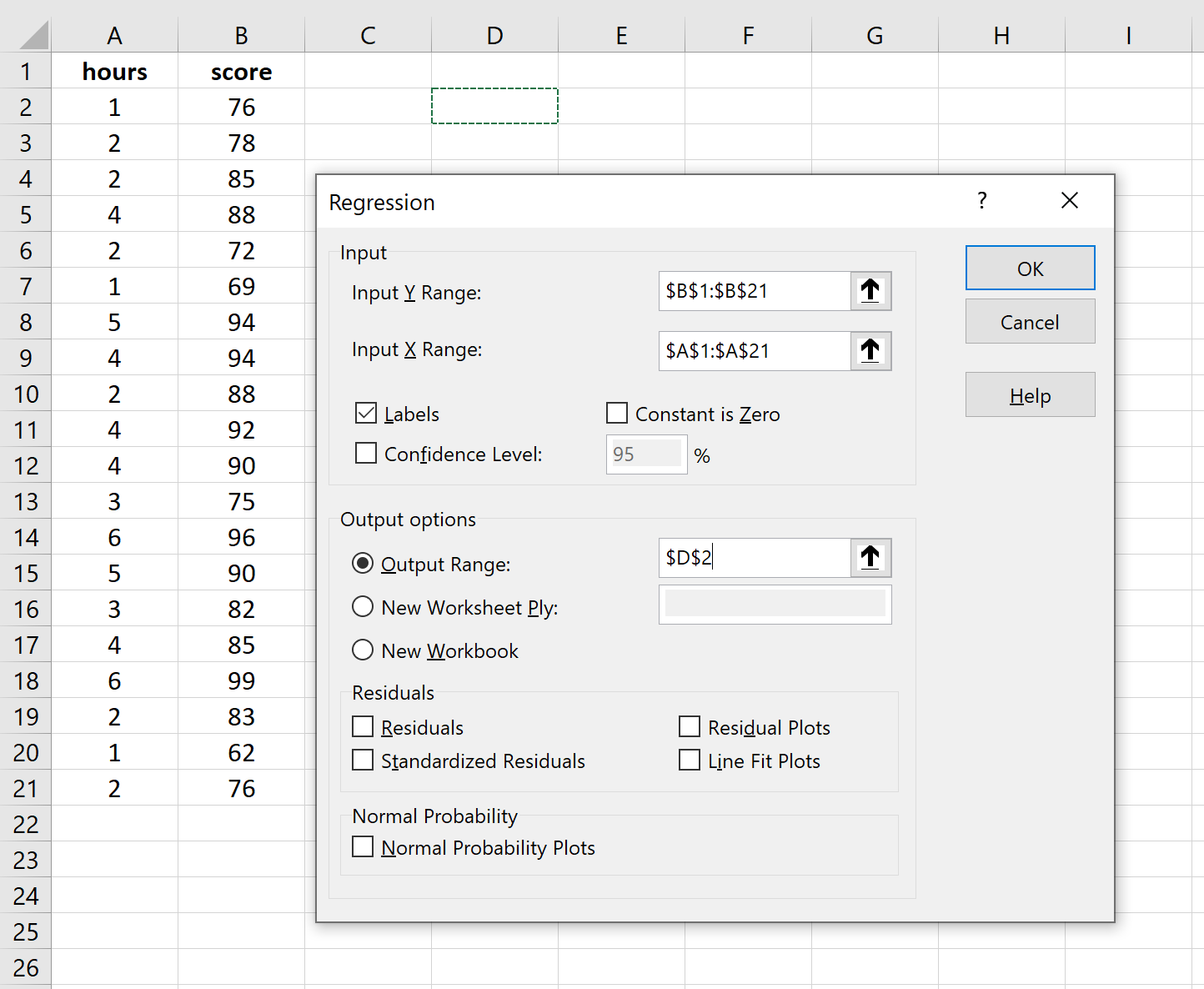
Автоматически появится следующий вывод:

Шаг 4: Интерпретируйте результат.
Вот как интерпретировать наиболее релевантные числа в результате:
R Квадрат: 0,7273 . Это называется коэффициентом детерминации. Это доля дисперсии переменной отклика, которую можно объяснить объясняющей переменной. В этом примере 72,73% разницы в результатах экзамена объясняется количеством изученных часов.
Стандартная ошибка: 5.2805 . Это среднее расстояние между наблюдаемыми значениями и линией регрессии. В данном примере наблюдаемые значения отклоняются в среднем на 5,2805 единиц от линии регрессии.
Ф: 47,9952 . Это общая статистика F для регрессионной модели, рассчитанная как регрессионное MS/остаточное MS.
Значение F: 0,0000 . Это значение p, связанное с общей статистикой F. Это говорит нам, является ли регрессионная модель статистически значимой или нет. Другими словами, он сообщает нам, имеет ли объясняющая переменная статистически значимую связь с переменной ответа. В данном случае значение p меньше 0,05, что указывает на наличие статистически значимой связи между количеством изученных часов и оценкой, полученной на экзамене.
Коэффициенты. Коэффициенты дают нам числа, необходимые для написания расчетного уравнения регрессии. В этом примере предполагаемое уравнение регрессии:
Оценка экзамена = 67,16 + 5,2503*(часы)
Мы интерпретируем коэффициент часов так, что за каждый дополнительный учебный час экзаменационный балл должен увеличиться в среднем на 5,2503 . Мы интерпретируем коэффициент пересечения как означающий, что ожидаемый результат экзамена для студента, обучающегося ноль часов, составляет 67,16 .
Мы можем использовать это предполагаемое уравнение регрессии для расчета ожидаемого результата экзамена для студента на основе количества учебных часов.
Например, студент, который учится три часа, должен набрать на экзамене балл 82,91 :
Оценка экзамена = 67,16 + 5,2503*(3) = 82,91
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как создать остаточный график в Excel
Как построить интервал прогнозирования в Excel
Как создать график QQ в Excel