Процентиль, квартиль и квантиль: в чем разница?
Три термина, которые студенты часто путают в статистике, — это процентили, квартили и квантили.
Вот простое определение каждого из них:
Процентили: диапазон от 0 до 100.
Квартили: диапазон от 0 до 4.
Квантили: переход от любого значения к любому другому значению.
Обратите внимание, что процентили и квартили — это просто разновидности квантилей.
Некоторые типы квантилей даже имеют конкретные названия, в том числе:
- Четыре квантиля называются квартилями .
- Пять квантилей называются квинтилями .
- 8 квантилей называются октилиями .
- Десять квантилей называются децилями .
- 100 квантилей называются процентилями .
Обратите внимание, что процентили и квартили имеют следующую взаимосвязь:
- 0 процентиль = 0 квартиль (также называемый минимумом)
- 25-й процентиль = 1-й квартиль
- 50-й процентиль = 2-й квартиль (также называемый медианой)
- 75-й процентиль = 3-й квартиль
- 100-й процентиль = 4-й квартиль (также называемый максимумом)
Пример: поиск процентилей и квартилей
Предположим, у нас есть следующий набор данных с 20 значениями:

Используя статистическое программное обеспечение (например, Excel, R, Python и т. д.), мы можем найти следующие процентили и квартили для этого набора данных:
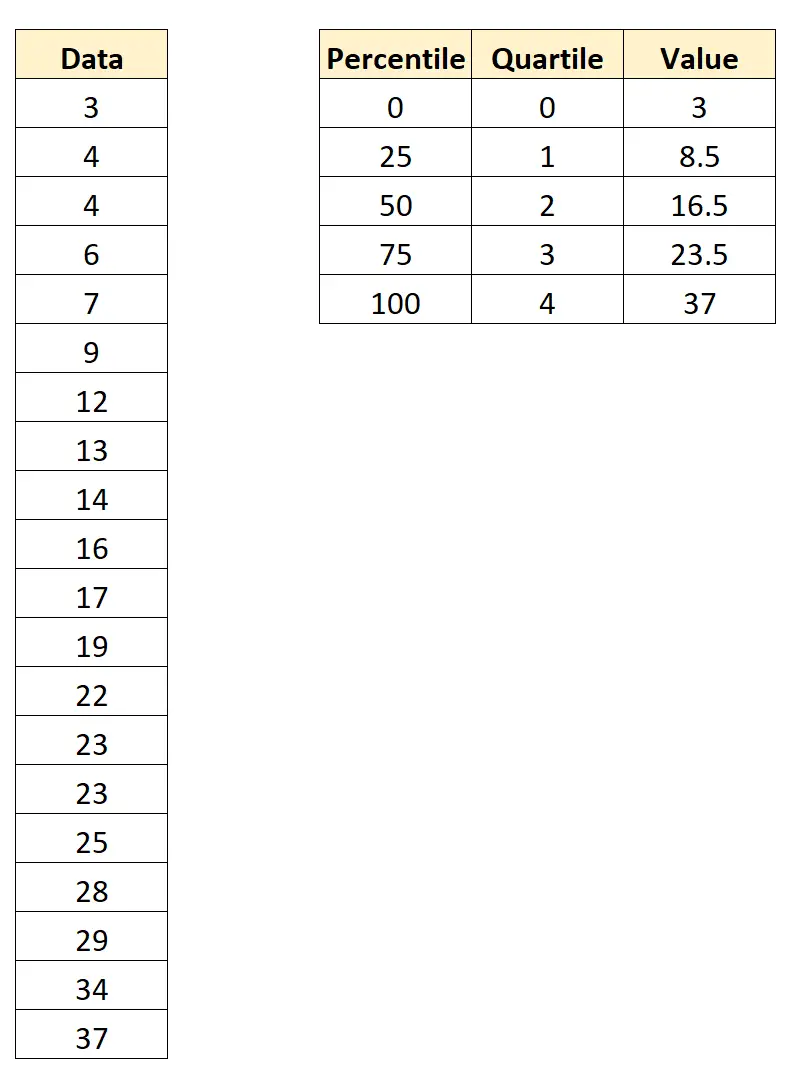
Вот как интерпретировать эти значения:
- Процентиль 0 и квартиль 0 равны 3 .
- 25-й процентиль и 1-й квартиль составляют 8,5 .
- 50-й процентиль и 2-й квартиль составляют 16,5 .
- 75-й процентиль и 3-й квартиль составляют 23,5 .
- 100-й процентиль и 4-й квартиль равны 37 .
Когда использовать процентили, а не квартили
Процентили можно использовать для ответа на такие вопросы, как:
Сколько студенту нужно набрать по конкретному тесту, чтобы попасть в 10% лучших?
Чтобы ответить на этот вопрос, мы должны найти 90-й процентиль всех оценок, который представляет собой значение, отделяющее 90% нижних от 10% верхних.
Какой рост составляет 40% среднего роста учащихся конкретной школы?
Чтобы ответить на этот вопрос, мы должны найти 70-й процентиль роста и 30-й процентиль роста, которые представляют собой два значения, которые определяют верхнюю и нижнюю границы для средних 40% роста.
Квартили можно использовать для ответа на такие вопросы, как:
Сколько студент должен набрать на тесте, чтобы попасть в четверть лучших?
Чтобы ответить на этот вопрос, мы должны найти третий квартиль всех оценок, который представляет собой значение, отделяющее нижние 75% от верхних 25%.
Каков межквартильный размах данного набора данных?
Межквартильный размах (IQR) — это диапазон средних 50% значений данных. Чтобы найти IQR для данного набора данных, мы можем вычислить 3-й квартиль – 1-й квартиль.
Дополнительные ресурсы
Как рассчитать процентили в R
Как посчитать квартили в R
Как рассчитать межквартильный размах в Excel
Как рассчитать межквартильный размах на калькуляторе TI-84