Размер образца

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое размер выборки и почему он важен в статистике. Кроме того, вы узнаете, как рассчитать соответствующий размер выборки, и решите упражнение, чтобы увидеть, как это делается.

Каков размер выборки?

Размер выборки (или размер выборки ) — это количество людей, составляющих выборку исследования. В статистике важен размер выборки, чтобы выборка была репрезентативной для всей совокупности.

Следовательно, размер выборки статистического исследования должен быть достаточно большим, чтобы отражать характеристики всей совокупности. С другой стороны, размер выборки не может быть чрезмерно большим, поскольку в этом случае исследование становится более дорогим. В заключение следует отметить, что размер выборки должен быть адекватным, не слишком большим и не слишком маленьким.

Например, если мы хотим провести анализ высоты страны, мы не можем запросить рост всех жителей страны, потому что опрос займет много времени и будет слишком дорогим. Поэтому необходимо провести случайную выборку и опросить только репрезентативную выборку населения.

➤ См.: Типы выборки.

И как мы можем узнать подходящий размер выборки? В следующем разделе мы увидим, как определить подходящий размер выборки на основе требований исследования.

Как рассчитать размер выборки

Для оценки среднего требуемый размер выборки равен квадрату Z _α/2 , умноженному на стандартное отклонение (σ), деленное на желаемую погрешность (e). Таким образом , формула для расчета размера выборки выглядит следующим образом:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Золото:

$n$

это размер выборки.
$\alpha$

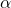
желаемый уровень значимости. Принимая во внимание это

$1-\alpha$

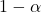
желаемый уровень доверия.
$Z_{\alpha/2}$

— квантиль стандартного нормального распределения, соответствующий вероятности α/2. Для больших размеров выборки и уровня достоверности 95% оно обычно близко к 1,96, а для уровня достоверности 99% оно обычно близко к 2,576.
$\sigma$

является стандартным отклонением.

Имейте в виду, что в этой формуле предполагается, что размер популяции бесконечен, то есть размер популяции очень велик или неизвестен.

Примечание. Приведенная выше формула получена на основе интервала доверительной формулы для среднего значения .

Пример расчета размера выборки

В этом разделе в качестве примера мы рассчитаем соответствующий размер выборки для статистического обследования.

Мы знаем, что стандартное отклонение популяции составляет около 15, но мы не знаем его среднего значения, поэтому мы хотим провести исследование, чтобы оценить среднее значение. Какой размер выборки нам нужен, если мы хотим, чтобы погрешность составляла ±2 с уровнем достоверности 95%?

Как мы видели выше, формула для расчета размера выборки:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

В этом случае желаемый уровень достоверности составляет 95%, поэтому соответствующее значение Z _α/2 равно 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ См.: Таблица значений уровня достоверности.

Наконец, теперь, когда мы знаем, сколько стоят все параметры, подставляем их значения в формулу и вычисляем размер выборки:

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

Короче говоря, чтобы оценить среднее значение популяции с желаемыми требованиями, нам нужна выборка как минимум из 217 человек.

Размер выборки, уровень достоверности и погрешность

В зависимости от уровня достоверности и требуемой погрешности требуемый размер выборки будет варьироваться. Таким образом, размер выборки, уровень достоверности и погрешность связаны следующим образом:

Размер выборки и уровень достоверности прямо пропорциональны. То есть, если уровень достоверности увеличится, размер выборки также увеличится.
Размер выборки и погрешность обратно пропорциональны. Таким образом, если погрешность увеличится, размер выборки уменьшится.
Следовательно, увеличение размера выборки может повысить уровень достоверности или уменьшить погрешность.

Другие формулы размера выборки

В зависимости от оцениваемого параметра формула необходимого размера выборки незначительно меняется. Поэтому в этом разделе мы увидим другие формулы, которые могут быть полезны для расчета размера выборки в некоторых особых случаях.

размер выборки доли

Формула для расчета размера выборки, необходимой для оценки доли (p):

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

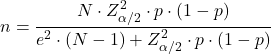
Размер выборки вероятности

Если вы хотите оценить вероятность, рекомендуется использовать следующую формулу для определения необходимого размера выборки:

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

Размер выборки для сравнения двух независимых средних значений

Формула расчета размера выборки при сравнении двух независимых средних значений с заданным риском α и риском β выглядит следующим образом:

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Золото

$\Delta$

это разница между двумя средствами альтернативной гипотезы.

Размер выборки для сравнения двух парных средних значений

Если вы хотите сравнить два парных средних значения с фиксированной ошибкой α и ошибкой β, для определения количества наблюдений в выборке следует использовать следующую формулу:

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Золото

$\Delta$

это разница между двумя парными средними альтернативной гипотезы и

$\sigma_d^2$

Это дисперсия различий между двумя измерениями одного и того же человека.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше