4 примера использования тестов хи-квадрат в реальной жизни
В статистике существует два разных типа тестов хи-квадрат:
1. Критерий согласия хи-квадрат – используется для определения того, соответствует ли категориальная переменная гипотетическому распределению.
2. Критерий независимости хи-квадрат – используется для определения наличия значимой связи между двумя категориальными переменными.
В этой статье мы приведем несколько примеров того, как каждый из этих типов тестов хи-квадрат используется в реальных ситуациях.
Пример 1: Критерий согласия хи-квадрат
Предположим, владелец магазина утверждает, что в его магазин каждый день недели приходит одинаковое количество покупателей.
Чтобы проверить эту гипотезу, он записывает количество покупателей, пришедших в магазин за данную неделю, и обнаруживает следующее:
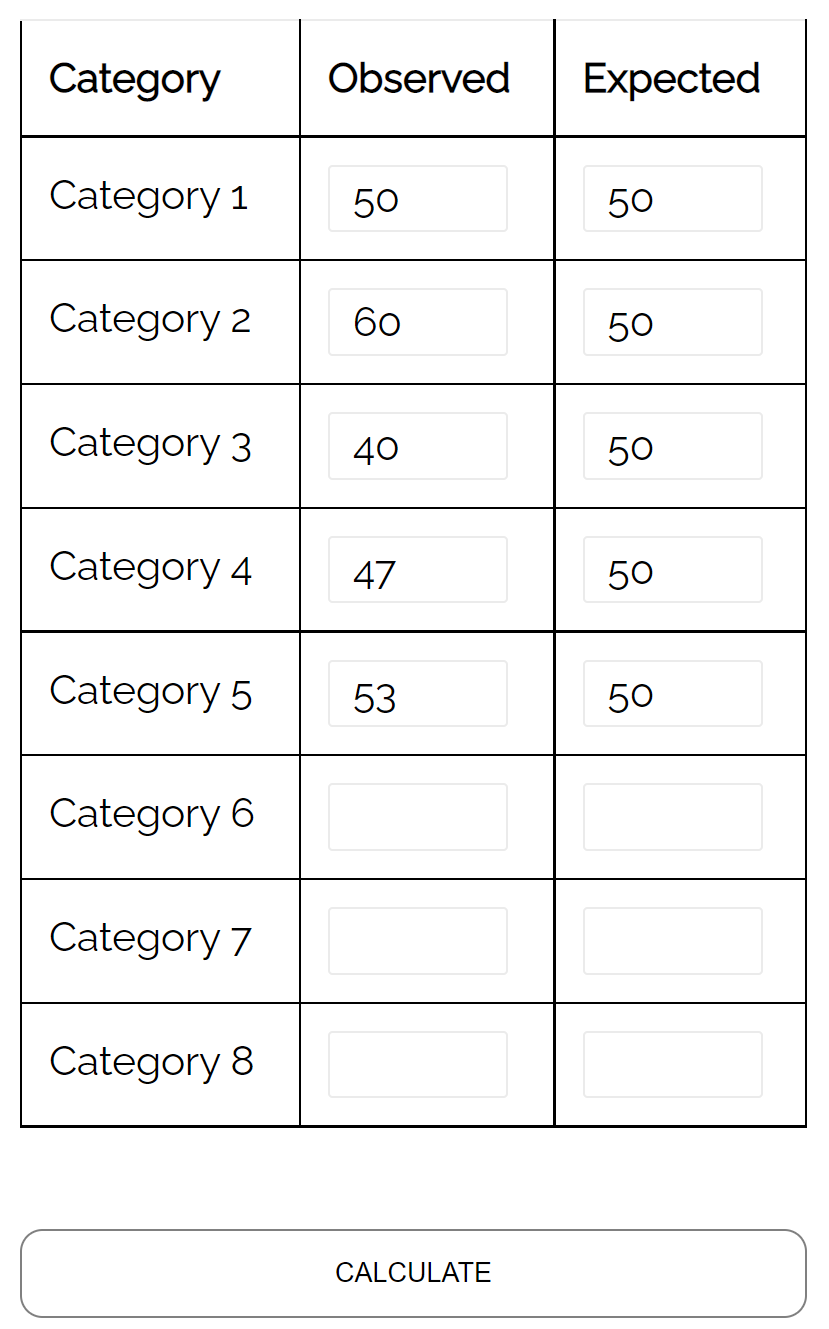
- Понедельник: 50 клиентов
- Вторник: 60 клиентов
- Среда: 40 клиентов
- Четверг: 47 клиентов
- Пятница: 53 клиента
Он может использовать критерий согласия хи-квадрат, чтобы определить, соответствует ли распределение клиентов, которые приходят каждый день, его гипотезе распределения.
Используя калькулятор критерия согласия хи-квадрат , он видит, что значение p теста составляет 0,359 .

Поскольку это значение p не меньше 0,05, нет достаточных доказательств, чтобы утверждать, что истинное распределение покупателей отличается от того, которое утверждает владелец магазина.
Пример 2: Критерий согласия хи-квадрат
Предположим, биолог утверждает, что равное количество оленей четырех разных видов каждую неделю заходит на определенный участок леса.
Чтобы проверить эту гипотезу, она записывает количество оленей каждого вида, заходящих в лесной массив в течение недели:
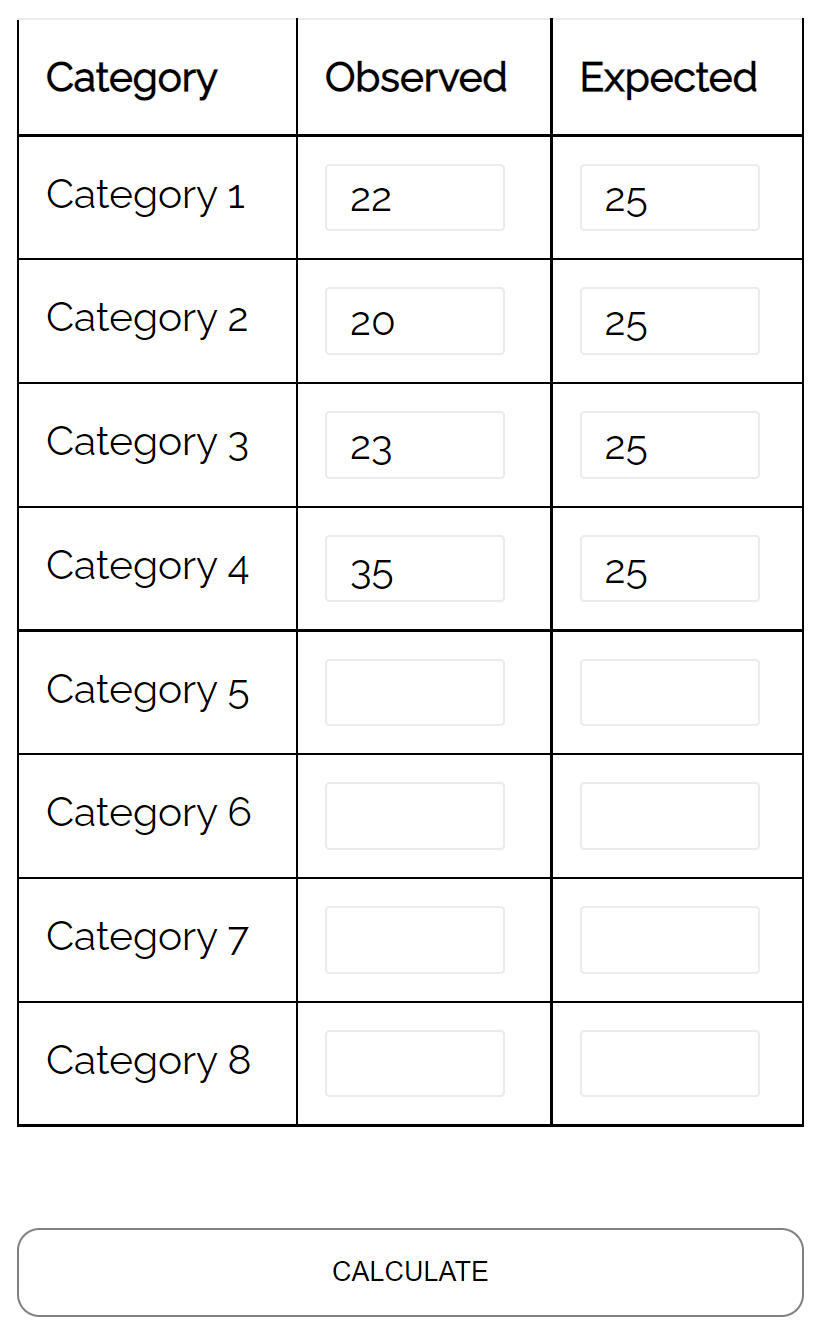
- Вид № 1: 22
- Вид № 2: 20
- Вид №3: 23
- Вид № 4: 35
Она может использовать критерий согласия хи-квадрат, чтобы определить, соответствует ли распределение видов оленей, которые каждую неделю попадают в лесную зону леса, с их гипотетическим распределением.
Используя калькулятор критерия согласия хи-квадрат , она видит, что значение p для теста составляет 0,137 .
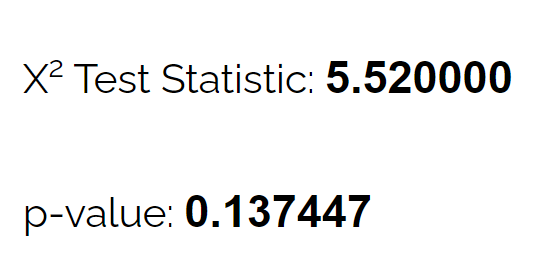
Поскольку это значение p не меньше 0,05, нет достаточных доказательств, чтобы утверждать, что истинное распространение оленей отличается от того, которое утверждает биолог.
Пример 3: Тест независимости по хи-квадрату
Предположим, что политик в определенном городе хочет знать, связан ли пол с предпочтениями политической партии.
Он решает взять простую случайную выборку из 500 избирателей и спросить их об их предпочтениях в отношении политических партий. В следующей таблице представлены результаты опроса:
| республиканец | Демократ | Независимый | Общий | |
| Мужской | 120 | 90 | 40 | 250 |
| Женский | 110 | 95 | 45 | 250 |
| Общий | 230 | 185 | 85 | 500 |
Он может использовать критерий независимости хи-квадрат , чтобы определить, существует ли статистически значимая связь между двумя переменными.
Используя калькулятор теста независимости хи-квадрат , он видит, что p-значение теста составляет 0,649 .
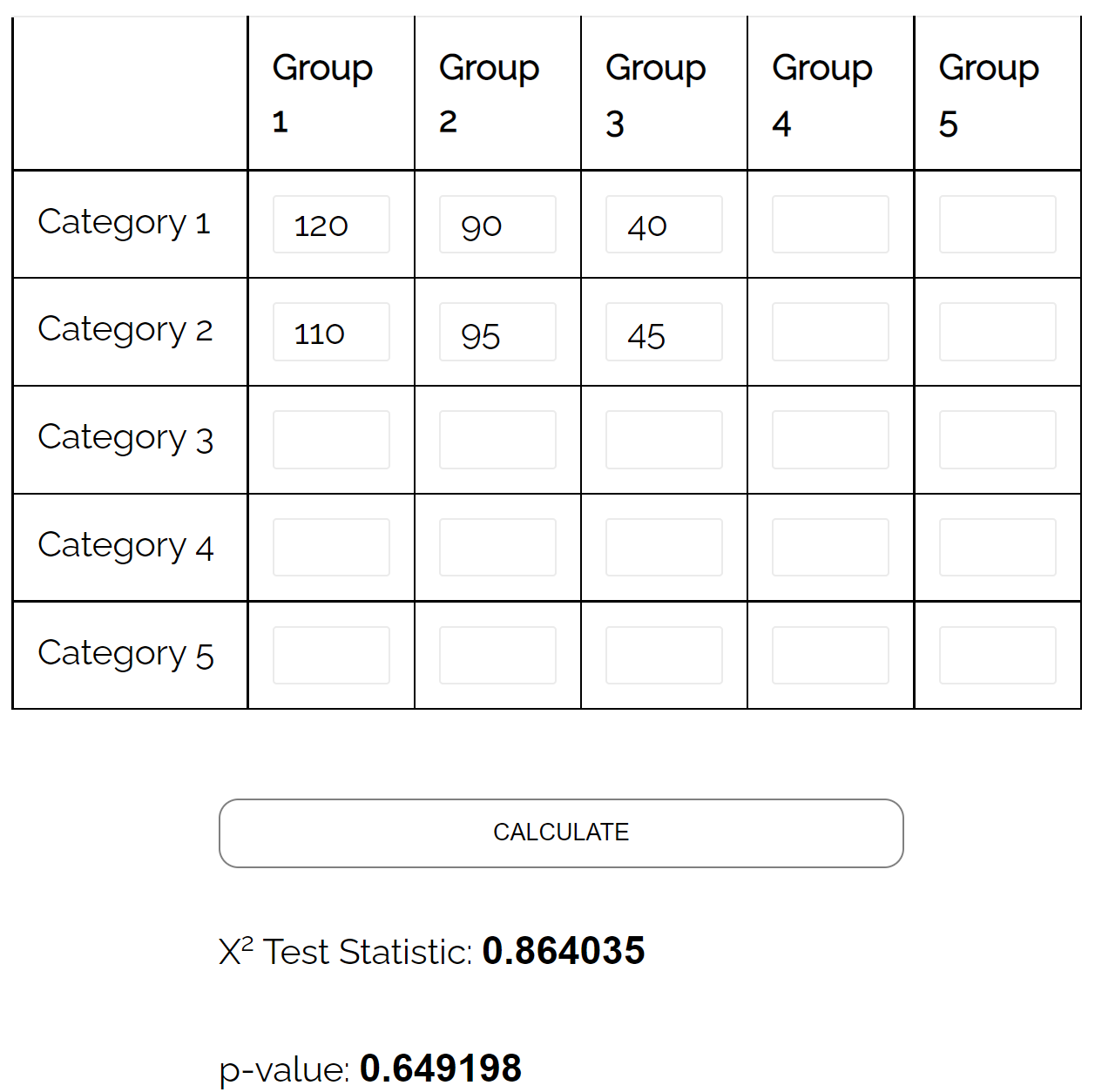
Поскольку значение p составляет не менее 0,05, нет достаточных доказательств того, что существует связь между полом и предпочтениями политических партий.
Пример 4: Проверка независимости по хи-квадрату
Предположим, исследователь хочет знать, связано ли семейное положение с уровнем образования.
Он решает взять простую случайную выборку из 300 человек и получает следующие результаты:
| Средняя школа | Бакалавриат | Магистр или выше | Общий | |
| Женатый | 20 | 100 | 35 | 155 |
| Холостяк | 50 | 80 | 15 | 145 |
| Общий | 70 | 180 | 50 | 300 |
Он может использовать критерий независимости хи-квадрат , чтобы определить, существует ли статистически значимая связь между двумя переменными.
Используя калькулятор теста независимости хи-квадрат , он видит, что p-значение теста равно 0,000011 .
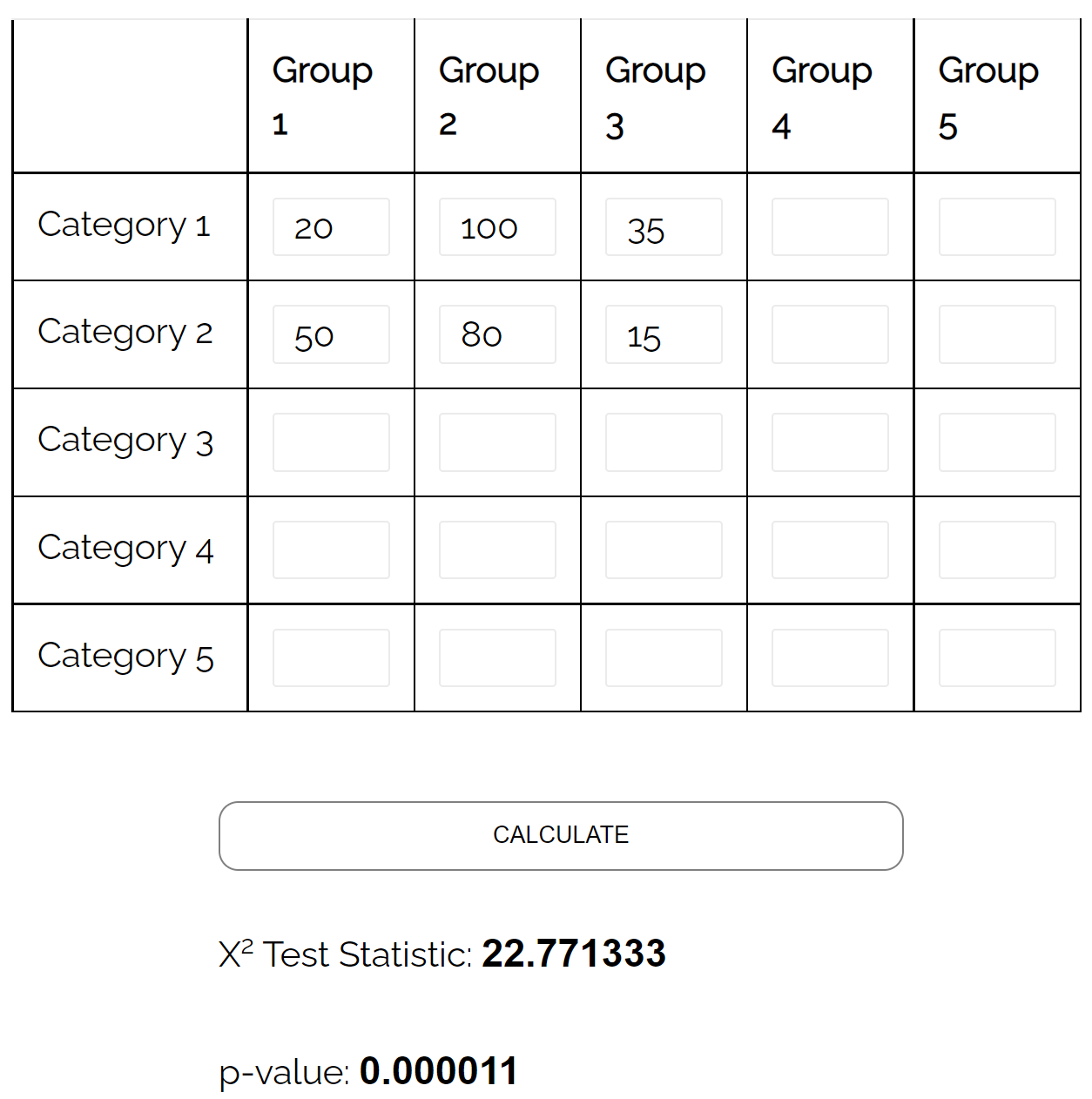
Поскольку значение p меньше 0,05, имеется достаточно доказательств того, что существует связь между семейным положением и уровнем образования.
Дополнительные ресурсы
Следующие учебные пособия знакомят с различными типами тестов хи-квадрат:
В следующих руководствах объясняется разница между тестами хи-квадрат и другими статистическими тестами: