Симметричное распределение: определение + примеры

В статистике симметричное распределение — это распределение, в котором левая и правая части зеркально отражают друг друга.

Самым известным симметричным распределением является нормальное распределение , имеющее отчетливую колоколообразную форму.

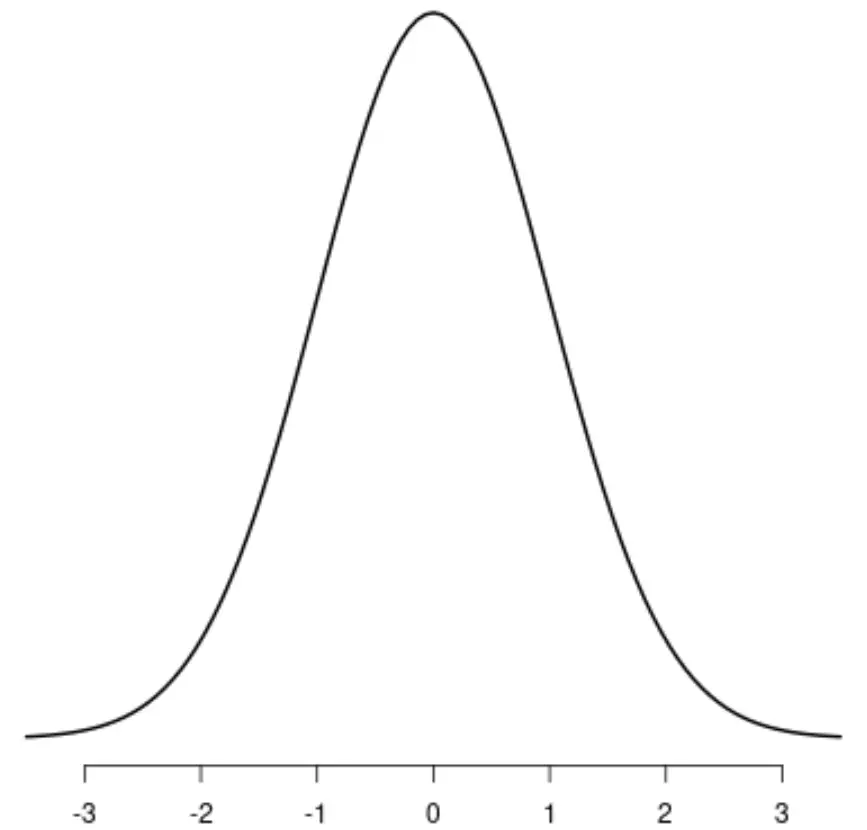
Если бы вы провели линию по центру распределения, левая и правая стороны распределения были бы идеально зеркальными:

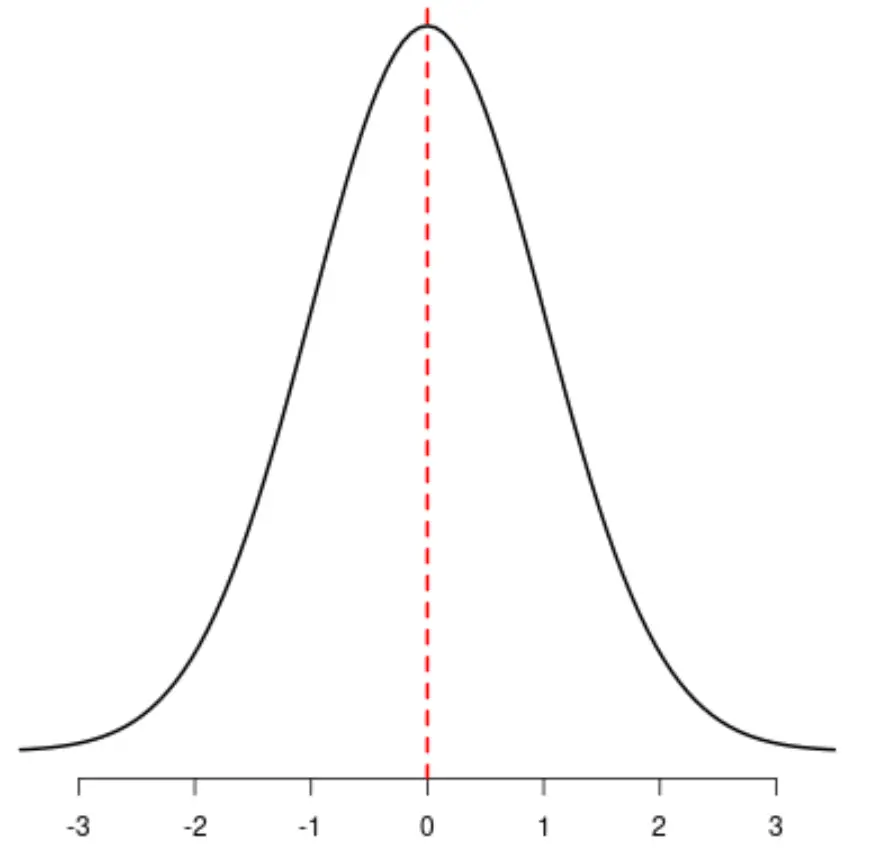
В статистике асимметрия — это способ описания симметрии распределения. Это значение может быть отрицательным, нулевым или положительным.

Для симметричных распределений асимметрия равна нулю.

Это контрастирует с левыми распределениями, которые имеют отрицательную асимметрию:

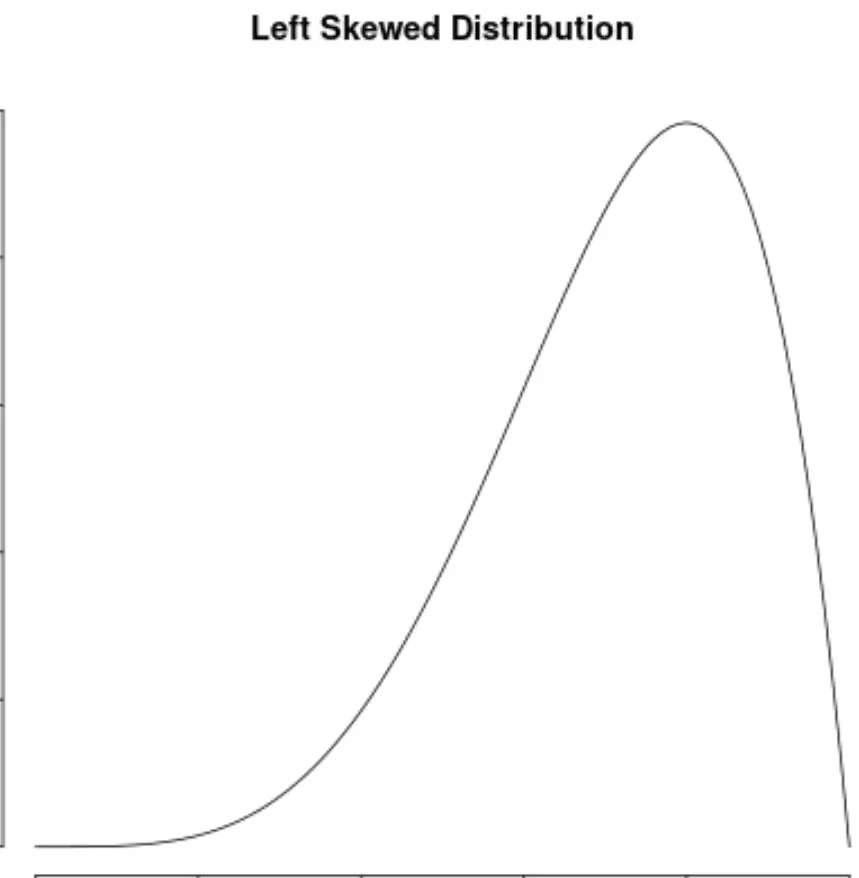
Это также контрастирует с распределениями с перекосом вправо, которые имеют положительную асимметрию:

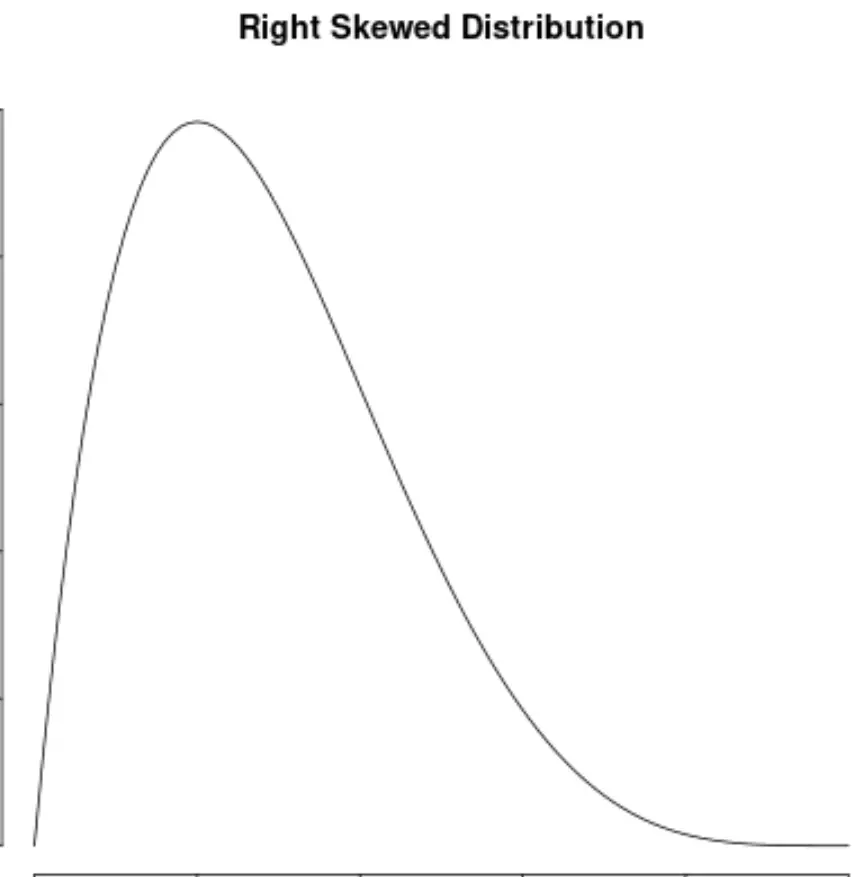
Свойства симметричных распределений

В симметричном распределении среднее значение, медиана и мода равны.

Запомните следующие определения для каждого из них:

• Среднее: среднее значение.
• Медиана: среднее значение.
• Режим: значение, которое появляется чаще всего.

При симметричном распределении каждое из этих значений равно другому.

До сих пор в каждом из примеров мы использовали в качестве примеров унимодальные распределения – распределения только с одним «пиком». Однако распределение также может быть бимодальным и симметричным.

Бимодальное распределение – это распределение, имеющее два максимума.

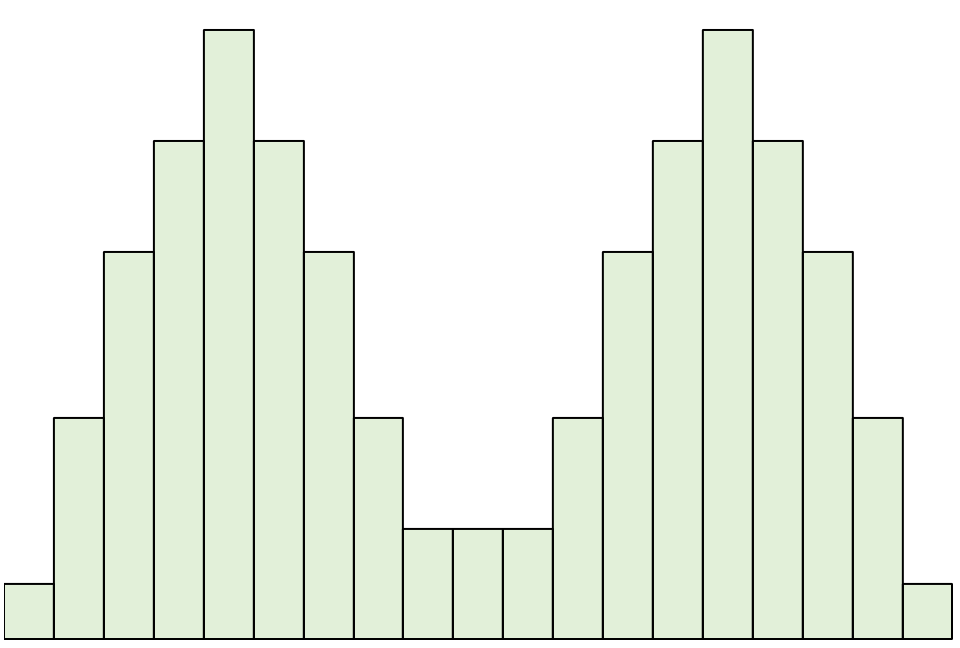
Обратите внимание: если мы проведем линию по центру этого распределения, левая и правая стороны все равно будут зеркально отражать друг друга.

Для этих распределений среднее и медиана равны. Однако мода лежит в обеих вершинах.

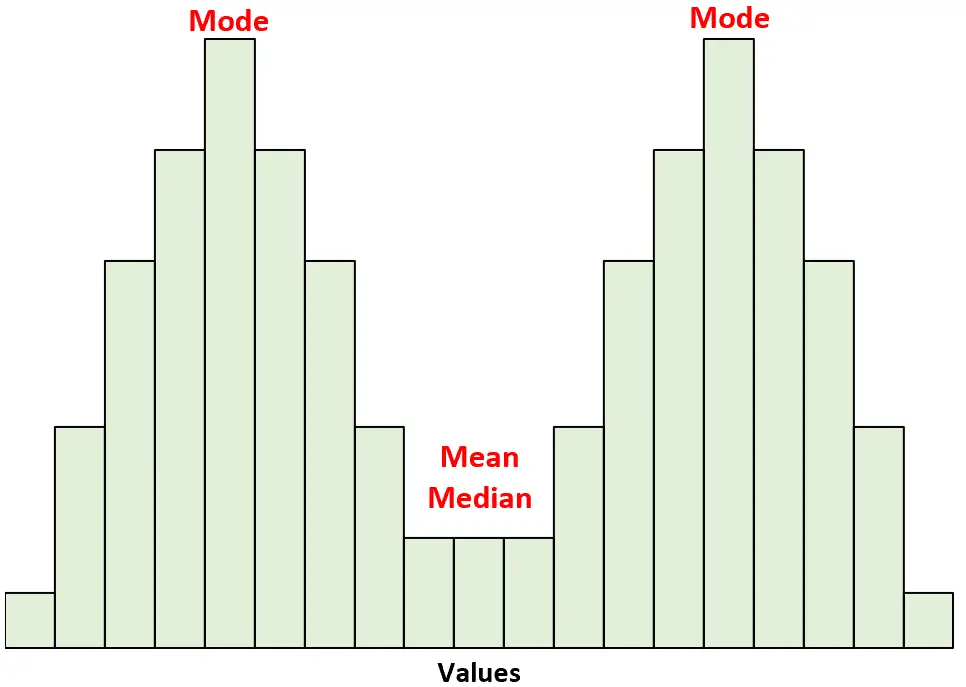
Другие примеры симметричных распределений

Помимо нормального распределения, следующие распределения также являются симметричными:

Распределение t

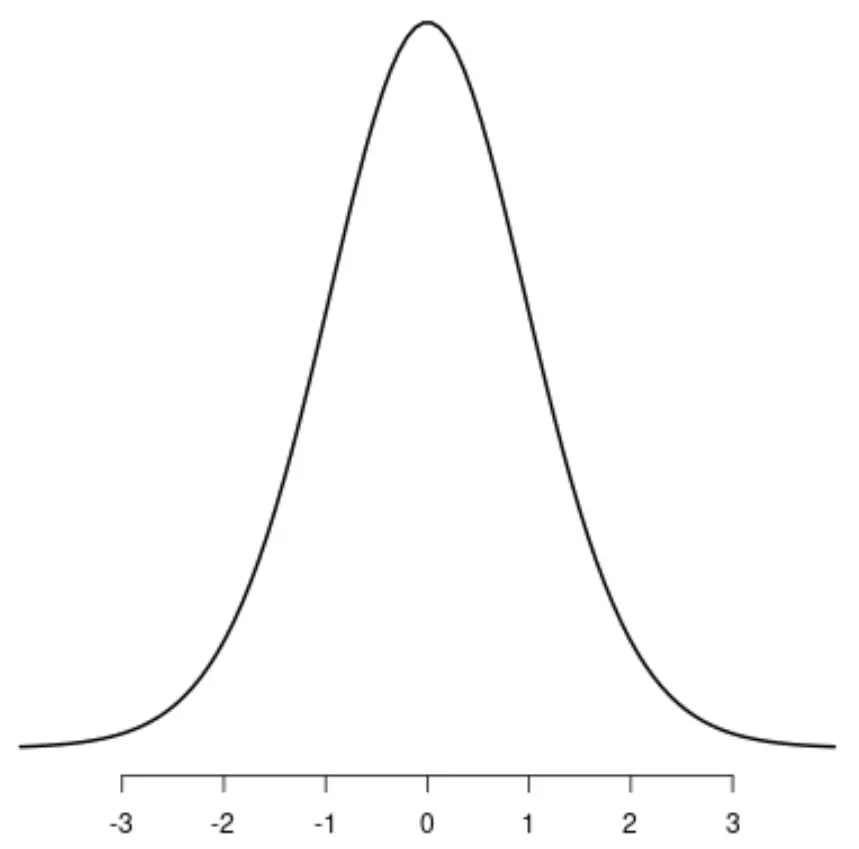
Равномерное распределение

Распределение Коши

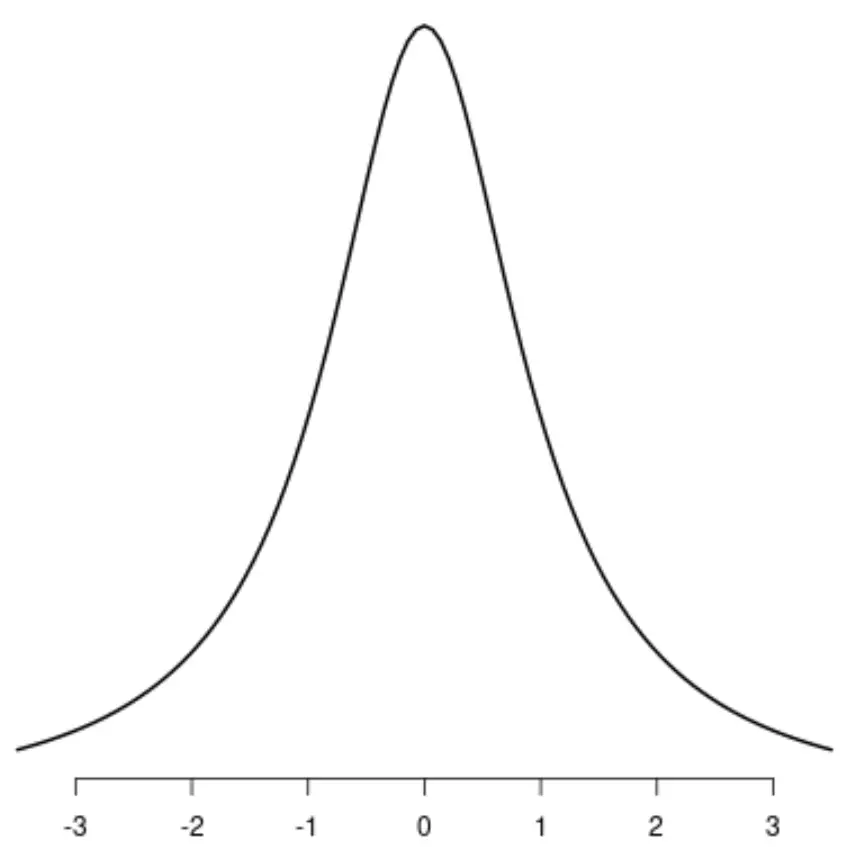
Если вы проведете линию по центру одного из этих распределений, левая и правая стороны каждого распределения будут идеально отражать друг друга.

Симметричные распределения и центральная предельная теорема

Одной из наиболее важных теорем во всей статистике является центральная предельная теорема, которая утверждает, что выборочное распределение выборочного среднего примерно нормально, если размер выборки достаточно велик, даже если распределение совокупности не является нормальным .

Чтобы применить центральную предельную теорему, размер выборки должен быть достаточно большим. Оказывается, сколько именно людей «достаточно большие» зависит от основной формы распределения населения.

Особенно:

• Если распределение населения симметрично, иногда достаточно небольшого размера выборки, составляющего 15 человек.
• Если распределение населения неравномерное, обычно необходима выборка не менее 30 человек.
• Если распределение населения крайне неравномерно, может потребоваться выборка из 40 и более человек.

Таким образом, преимущество симметричных распределений состоит в том, что нам нужны меньшие размеры выборки, чтобы применить центральную предельную теорему при расчете доверительных интервалов или выполнении проверки гипотез .

Дополнительные ресурсы

Введение в центральную предельную теорему
Что такое бимодальное распределение?
Руководство по асимметричным распределениям влево и вправо