Сплайны многомерной адаптивной регрессии в r
Сплайны многомерной адаптивной регрессии (MARS) можно использовать для моделирования нелинейных связей между набором переменных-предикторов и переменной отклика .
Этот метод работает следующим образом:
1. Разделите набор данных на k частей.
2. Подобрать регрессионную модель к каждой части.
3. Используйте k-кратную перекрестную проверку, чтобы выбрать значение k .
В этом руководстве представлен пошаговый пример того, как подогнать модель MARS к набору данных в R.
Шаг 1. Загрузите необходимые пакеты
В этом примере мы будем использовать набор данных ISLR Wage . пакет, который содержит годовые зарплаты 3000 человек, а также различные переменные-предсказатели, такие как возраст, образование, раса и многое другое.
Прежде чем подогнать модель MARS к данным, мы загрузим необходимые пакеты:
library (ISLR) #contains Wage dataset library (dplyr) #data wrangling library (ggplot2) #plotting library (earth) #fitting MARS models library (caret) #tuning model parameters
Шаг 2. Просмотр данных
Далее мы отобразим первые шесть строк набора данных, с которым работаем:
#view first six rows of data
head (Wage)
year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574
Шаг 3. Создайте и оптимизируйте модель MARS.
Далее мы создадим модель MARS для этого набора данных и выполним k-кратную перекрестную проверку , чтобы определить, какая модель дает наименьшее тестовое RMSE (среднеквадратическая ошибка).
#create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
nprune = seq (2, 50, length.out = 10) %>%
floor ())
#make this example reproducible
set.seed(1)
#fit MARS model using k-fold cross-validation
cv_mars <- train(
x = subset(Wage, select = -c(wage, logwage)),
y = Wage$wage,
method = " earth ",
metric = " RMSE ",
trControl = trainControl(method = " cv ", number = 10),
tuneGrid = hyper_grid)
#display model with lowest test RMSE
cv_mars$results %>%
filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554
Из результатов мы видим, что модель, которая дала наименьший тестовый MSE, была моделью только с эффектами первого порядка (т. е. без условий взаимодействия) и 12 членами. Эта модель дала среднеквадратическую ошибку (RMSE) 33,8164 .
Примечание. Мы использовали метод = «Земля» для указания модели MARS. Документацию по этому методу вы можете найти здесь .
Мы также можем создать диаграмму для визуализации теста RMSE на основе степени и количества терминов:
#display test RMSE by terms and degree
ggplot(cv_mars)
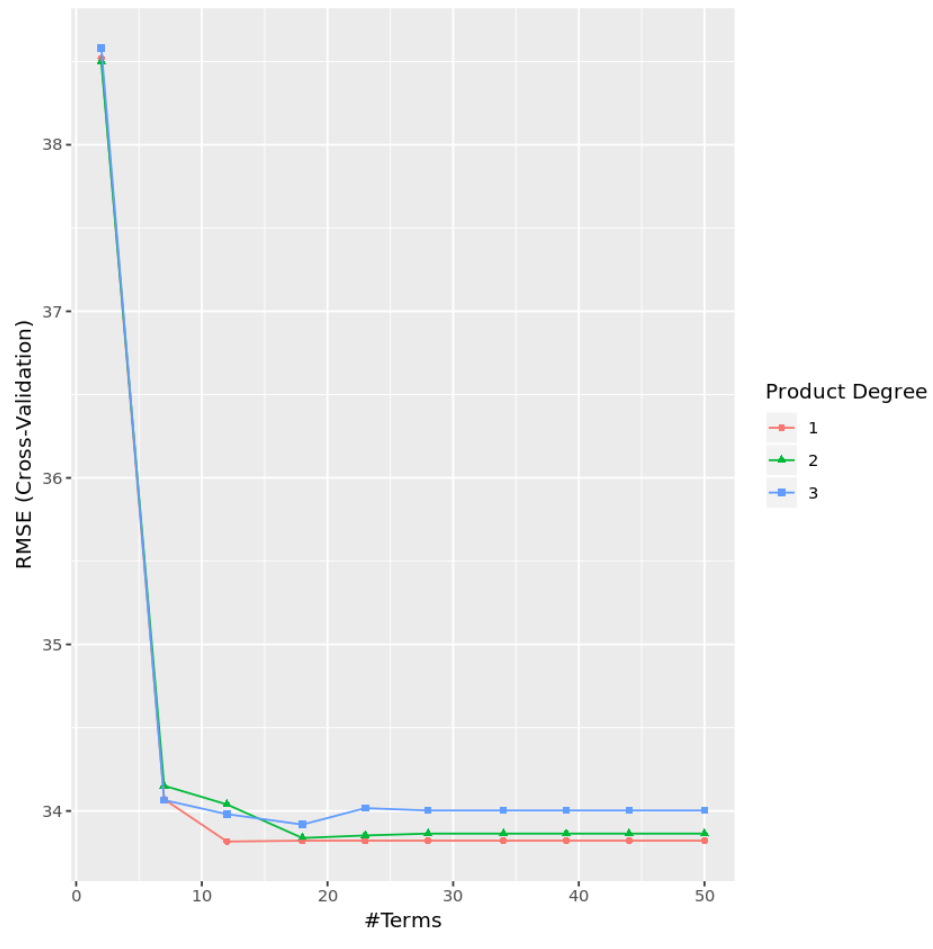
На практике мы бы адаптировали модель MARS с несколькими другими типами моделей, такими как:
- Множественная линейная регрессия
- Полиномиальная регрессия
- Пиковая регрессия
- Лассо-регрессия
- Регрессия главных компонентов
- Частичные наименьшие квадраты
Затем мы сравним каждую модель, чтобы определить, какая из них приводит к наименьшей ошибке тестирования, и выберем эту модель в качестве оптимальной для использования.
Полный R-код, использованный в этом примере, можно найти здесь .