Геометрические средства

К бенджамин андерсон 6 августа, 2023 Статистика 0 комментариев

В этой статье мы объясним, что такое среднее геометрическое, как оно рассчитывается и в чем разница между средним геометрическим и средним арифметическим. Вы также сможете увидеть пошаговое решение упражнения на среднее геометрическое и каковы свойства этого типа среднего. Наконец, вы найдете калькулятор для расчета среднего геометрического любого набора данных.

Что такое среднее геометрическое?

Среднее геометрическое является мерой центральности описательной статистики. Среднее геометрическое набора статистических данных равно корню n-й степени из произведения всех значений.

Среднее геометрическое используется в бизнес-финансах для расчета нормы прибыли, средних процентных значений и сложных процентов.

Таким образом, формула среднего геометрического выглядит следующим образом:

Среднее геометрическое можно рассчитать только в том случае, если все данные в выборке положительны. Потому что, если значение отрицательное, корень будет иметь отрицательное решение или не иметь решения, с другой стороны, если данные равны нулю, то умножение данных даст ноль и, следовательно, среднее геометрическое будет равно 0.

Среднее геометрическое — не единственный существующий тип среднего. Существуют также среднее арифметическое, средневзвешенное, среднее квадратическое и среднее гармоническое.

Разница между средним геометрическим и средним арифметическим

Основное отличие среднего геометрического от среднего арифметического состоит в том, что среднее геометрическое менее чувствительно к крайним значениям, чем среднее арифметическое. Кроме того, среднее арифметическое может рассчитываться с отрицательными и нулевыми значениями, а среднее геометрическое — только с положительными значениями.

Аналогично, среднее геометрическое обычно будет ниже среднего арифметического для того же набора данных.

Следует также отметить, что расчет среднего геометрического более сложен и, следовательно, его статистическую значимость труднее интерпретировать.

Короче говоря, среднее геометрическое имеет преимущества и недостатки по сравнению со средним арифметическим и, в зависимости от характера данных, будет уместно вычислять то или иное среднее.

Как вычислить среднее геометрическое

Для расчета среднего геометрического необходимо выполнить следующие действия:

Рассчитайте произведение всех статистических данных в выборке.
Найдите корень n-й степени из вычисленного произведения.
Полученный результат представляет собой среднее геометрическое статистической выборки.

Как видите, найти среднее геометрическое набора данных с помощью калькулятора или компьютерной программы относительно просто, поскольку вам нужно вычислить только произведение и корень. Наоборот, производить расчет вручную достаточно трудоемко.

👉 Вот почему мы рекомендуем использовать калькулятор ниже для расчета среднего геометрического набора данных.

Пример среднего геометрического значения

После того, как мы ознакомились с теорией среднего геометрического, мы приведем пример, чтобы вы могли точно понять, как получить среднее геометрическое.

Известны экономические результаты деятельности компании за последние пять лет. В первый год компания получила экономическую рентабельность 10%, во второй год прибыль достигла 23%, в третий год заработанные деньги составили 16%, в четвертый год она достигла экономической рентабельности 7%, а инвестиции за пятый год прибыль составила 20%. Вас просят вычислить среднее значение всех процентов.

Как мы видели, для расчета среднего значения процентов следует использовать не среднее арифметическое, а производить расчет со средним геометрическим.

Поэтому применим формулу среднего геометрического:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

И подставляем значения примера в формулу и выполняем расчет:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Обратите внимание, что у нас есть пять точек данных, поэтому мы вычисляем корень пятой степени.

Числовой результат среднего геометрического равен 1,15, что означает, что экономический рост компании в среднем составляет 15% каждый год.

Имейте в виду, что мы смогли получить среднее геометрическое, поскольку все значения были положительными, но если бы какой-либо процент был отрицательным, нам пришлось бы поместить данные в формулу в виде положительного десятичного числа с целой частью. равен нулю. Например, рост -30% следует выразить в формуле как 0,70 (1-0,3=0,7).

Калькулятор среднего геометрического значения

Подставьте любой пример статистики в калькулятор ниже, чтобы найти среднее геометрическое. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя. Помните, что вы не можете определить среднее геометрическое, если значение отрицательное или нулевое.

Свойства среднего геометрического

Среднее геометрическое имеет следующие характеристики:

Это тип среднего значения, который очень полезен для определения среднего значения процентов или индексов.

Его можно рассчитать только в том случае, если все данные положительны.

Геометрический смысл среднего геометрического двух чисел a и b — это сторона квадрата той же площади, что и прямоугольник, стороны которого равны a и b .

$MG(a,b)=\sqrt{a\cdot b}$

Геометрический смысл среднего геометрического трех чисел a , b и c — это сторона куба, объем которой эквивалентен параллелепипеду со сторонами a , b и c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Логарифм среднего геометрического набора данных дает среднее арифметическое логарифмов того же набора.

Среднее геометрическое набора значений всегда будет меньше или равно среднему арифметическому.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

Средневзвешенное геометрическое рассчитывается так же, как и среднее геометрическое, но путем добавления весов к показателю степени каждого элемента данных для взвешивания статистических значений.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

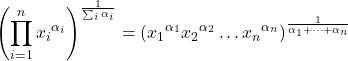
Вычислить среднее геометрическое в Excel

Наконец, давайте посмотрим, как найти среднее геометрическое набора данных с помощью программы Excel.

Чтобы вычислить среднее геометрическое в Excel, нужно использовать функцию СРЕДСТВ.ГЕОМ. Просто введите все значения, для которых вы хотите получить среднее геометрическое, и функция вернет результат среднего геометрического.

Например, чтобы определить среднее геометрическое в приведенном выше примере, вы должны написать в поле Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .

Следует иметь в виду, что если какое-либо из значений равно нулю или отрицательному значению, функция вернет ошибку.

Как видите, вычислить среднее геометрическое с помощью Excel гораздо проще и быстрее, так как вам достаточно скопировать данные на лист и использовать формулу.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше