Понимание стандартной ошибки наклона регрессии

Стандартная ошибка наклона регрессии — это способ измерения «неопределенности» в оценке наклона регрессии.

Он рассчитывается следующим образом:

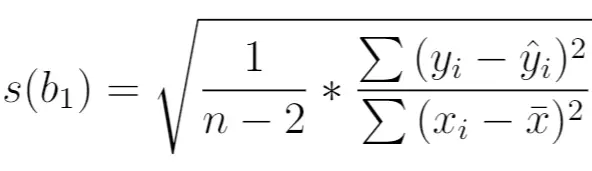
Золото:

• n : общий размер выборки
• y _i : реальное значение переменной ответа
• ŷ _i : прогнозируемое значение переменной ответа.
• x _i : реальное значение прогнозируемой переменной
• x̄ : среднее значение прогнозируемой переменной

Чем меньше стандартная ошибка, тем ниже изменчивость оценки коэффициента наклона регрессии.

Стандартная ошибка наклона регрессии будет отображаться в столбце «стандартная ошибка» в результатах регрессии большинства статистических программ:

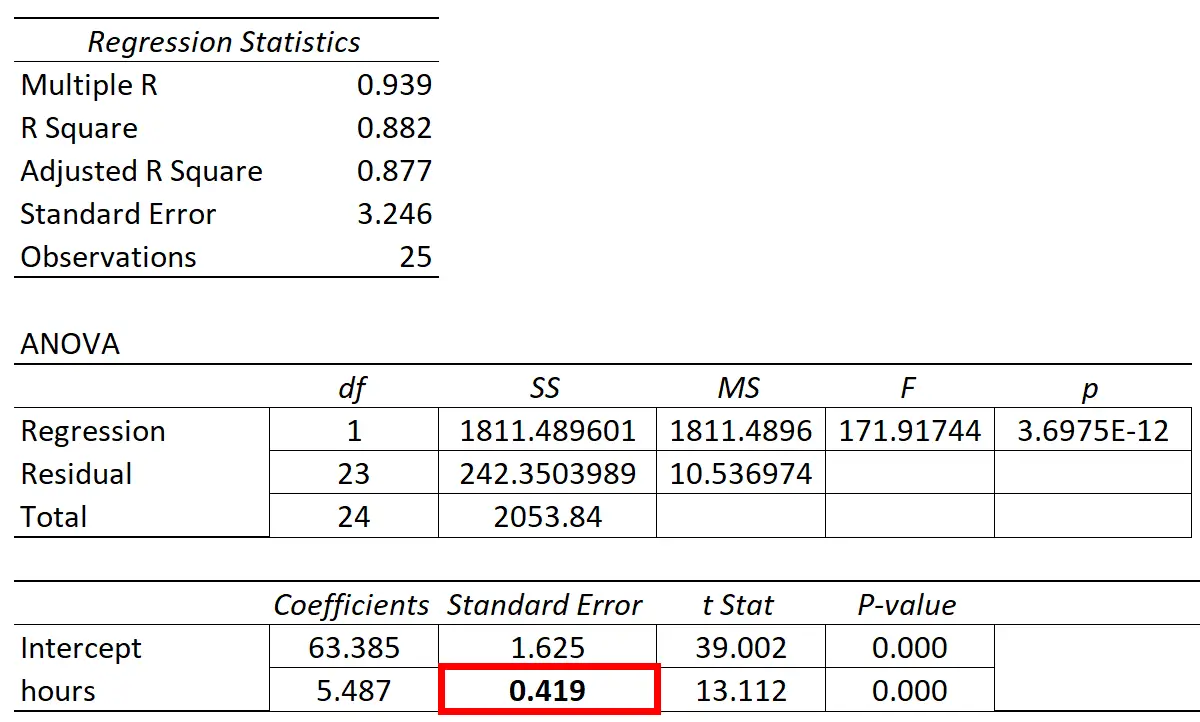
В следующих примерах показано, как интерпретировать стандартную ошибку наклона регрессии в двух разных сценариях.

Пример 1. Интерпретация небольшой стандартной ошибки наклона регрессии

Предположим, профессор хочет понять взаимосвязь между количеством учебных часов и итоговой оценкой на экзамене студентов его класса.

Он собирает данные по 25 студентам и создает следующую диаграмму рассеяния:

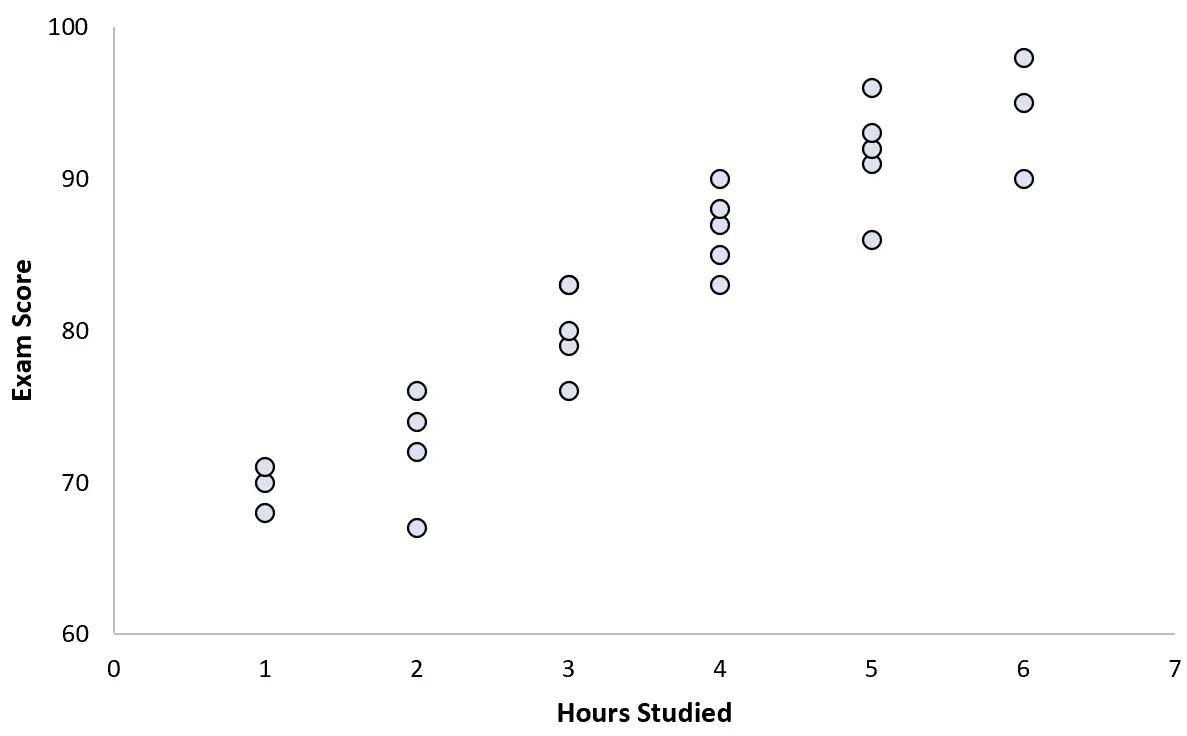
Между этими двумя переменными существует явно положительная связь. По мере увеличения количества изучаемых часов оценка на экзамене увеличивается с довольно предсказуемой скоростью.

Затем он подобрал простую модель линейной регрессии, используя часы обучения в качестве предикторной переменной и оценку на итоговом экзамене в качестве переменной ответа.

В следующей таблице показаны результаты регрессии:

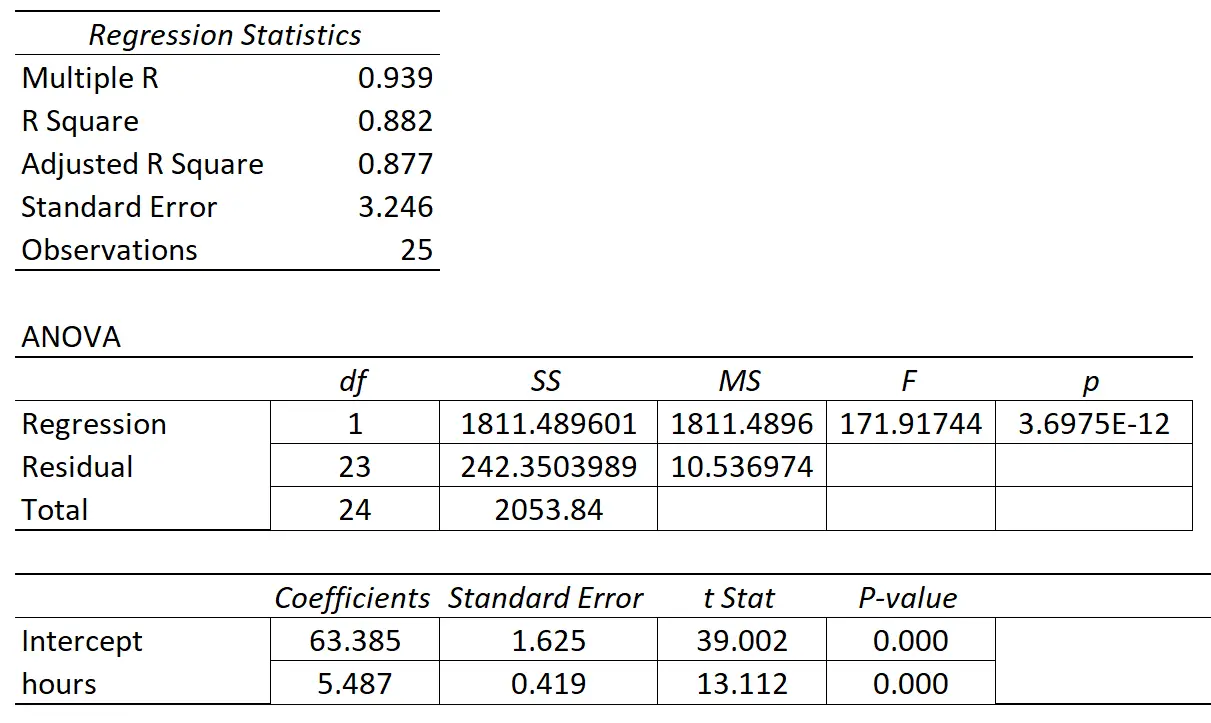
Коэффициент предикторной переменной «учебные часы» равен 5,487. Это говорит нам о том, что каждый дополнительный час обучения связан со средним увеличением экзаменационной оценки на 5487 баллов.

Стандартная ошибка составляет 0,419 , что представляет собой меру изменчивости этой оценки наклона регрессии.

Мы можем использовать это значение для расчета t-статистики для предикторной переменной «ученые часы»:

• t статистика = оценка коэффициента / стандартная ошибка
• t-статистика = 5,487/0,419
• t-статистика = 13,112

Значение p, соответствующее этой статистике теста, равно 0,000, что указывает на то, что количество учебных часов имеет статистически значимую связь с итоговой оценкой экзамена.

Поскольку стандартная ошибка наклона регрессии была небольшой по сравнению с оценкой коэффициента наклона регрессии, переменная-предиктор была статистически значимой.

Пример 2. Интерпретация большой стандартной ошибки наклона регрессии

Предположим, другой профессор хочет понять взаимосвязь между количеством учебных часов и итоговой оценкой на экзамене студентов его класса.

Она собирает данные о 25 студентах и создает следующую диаграмму рассеяния:

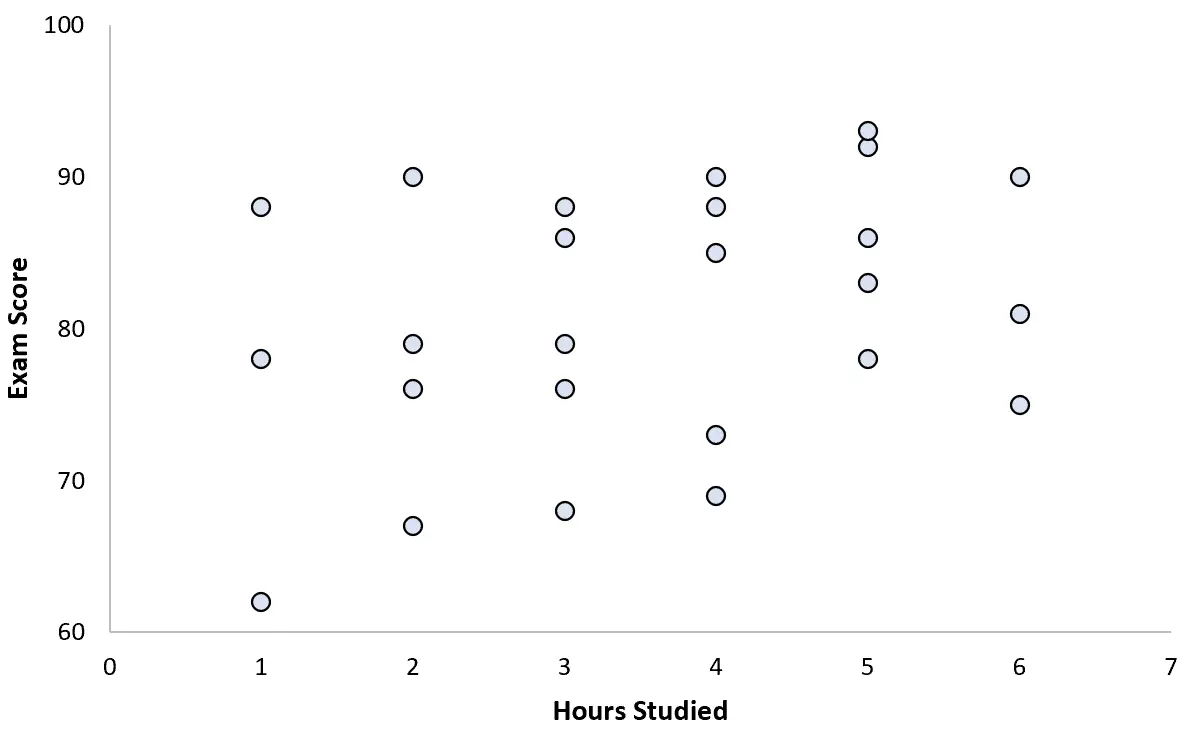
Кажется, между этими двумя переменными существует небольшая положительная связь. По мере увеличения количества учебных часов оценка на экзамене обычно увеличивается, но не с предсказуемой скоростью.

Предположим, что профессор затем подбирает простую модель линейной регрессии, используя часы обучения в качестве предикторной переменной и оценку на итоговом экзамене в качестве переменной ответа.

В следующей таблице показаны результаты регрессии:

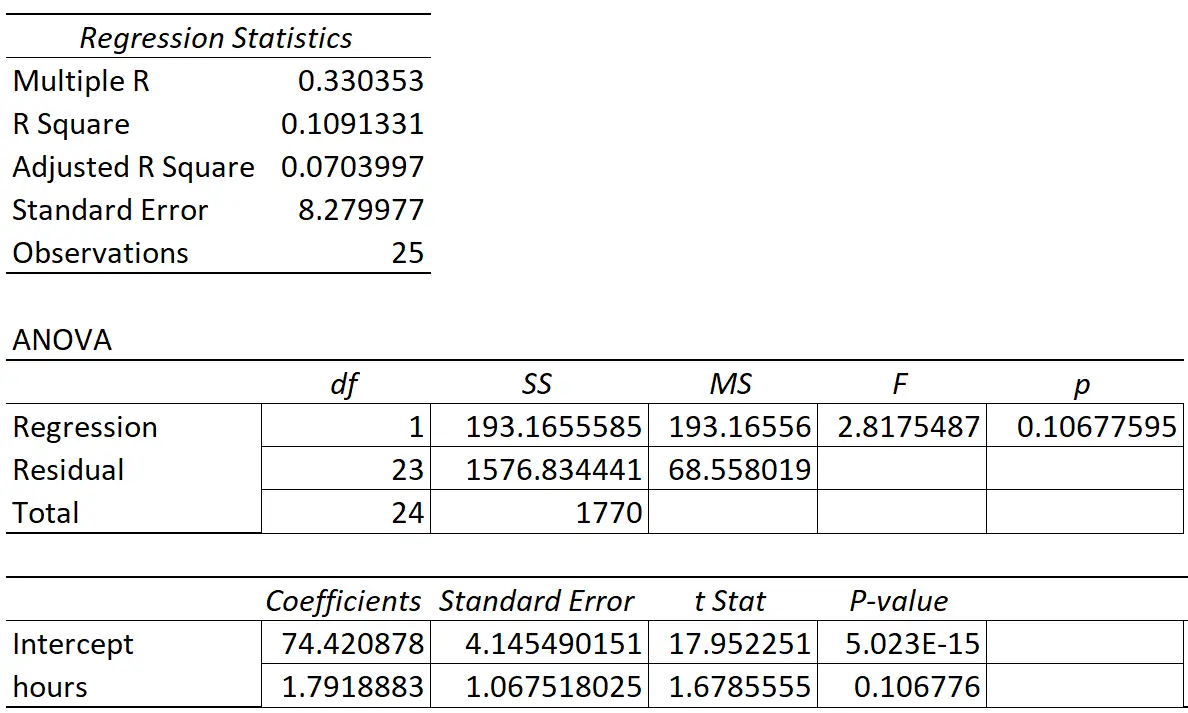
Коэффициент при предикторной переменной «часы обучения» равен 1,7919. Это говорит нам о том, что каждый дополнительный час обучения связан со средним увеличением экзаменационной оценки на 1,7919 .

Стандартная ошибка составляет 1,0675 , что является мерой изменчивости этой оценки наклона регрессии.

Мы можем использовать это значение для расчета t-статистики для предикторной переменной «ученые часы»:

• t статистика = оценка коэффициента / стандартная ошибка
• t-статистика = 1,7919/1,0675
• t-статистика = 1,678

Значение p, соответствующее этой тестовой статистике, составляет 0,107. Поскольку это значение p составляет не менее 0,05, это указывает на то, что количество учебных часов не имеет статистически значимой связи с оценкой итогового экзамена.

Поскольку стандартная ошибка наклона регрессии была большой по сравнению с оценкой коэффициента наклона регрессии, переменная-предиктор не была статистически значимой.

Дополнительные ресурсы

Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Как читать и интерпретировать таблицу регрессии