Как выполнить квадратичную регрессию в stata
Когда две переменные имеют линейную связь, вы часто можете использовать простую линейную регрессию для количественной оценки их связи.

Однако, когда две переменные имеют квадратичную связь, вы можете использовать квадратичную регрессию для количественной оценки их связи.

В этом руководстве объясняется, как выполнить квадратичную регрессию в Stata.
Пример: квадратичная регрессия в Stata
Предположим, мы хотим понять взаимосвязь между количеством отработанных часов и счастьем. У нас есть следующие данные о количестве отработанных часов в неделю и уровне счастья (по шкале от 0 до 100) для 16 разных людей:
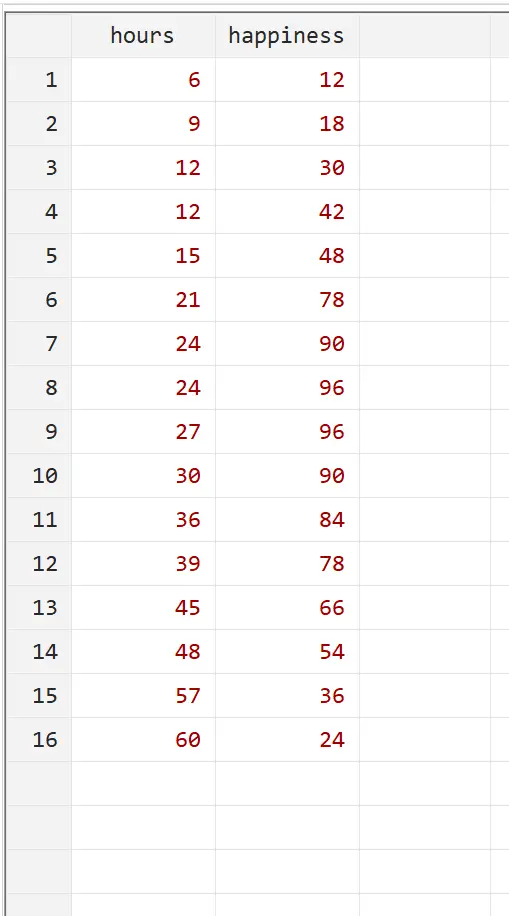
Вы можете воспроизвести этот пример, введя именно эти данные в Stata, используя Данные > Редактор данных > Редактор данных (Редактировать) в верхнем меню.
Используйте следующие шаги, чтобы выполнить квадратичную регрессию в Stata.
Шаг 1: Визуализируйте данные.
Прежде чем мы сможем использовать квадратичную регрессию, мы должны убедиться, что связь между объясняющей переменной (часы) и переменной ответа (счастье) действительно квадратичная. Итак, давайте визуализируем данные с помощью диаграммы рассеяния , введя следующее в поле «Команда»:
разогнать часы счастья
В результате получается следующая диаграмма рассеяния:
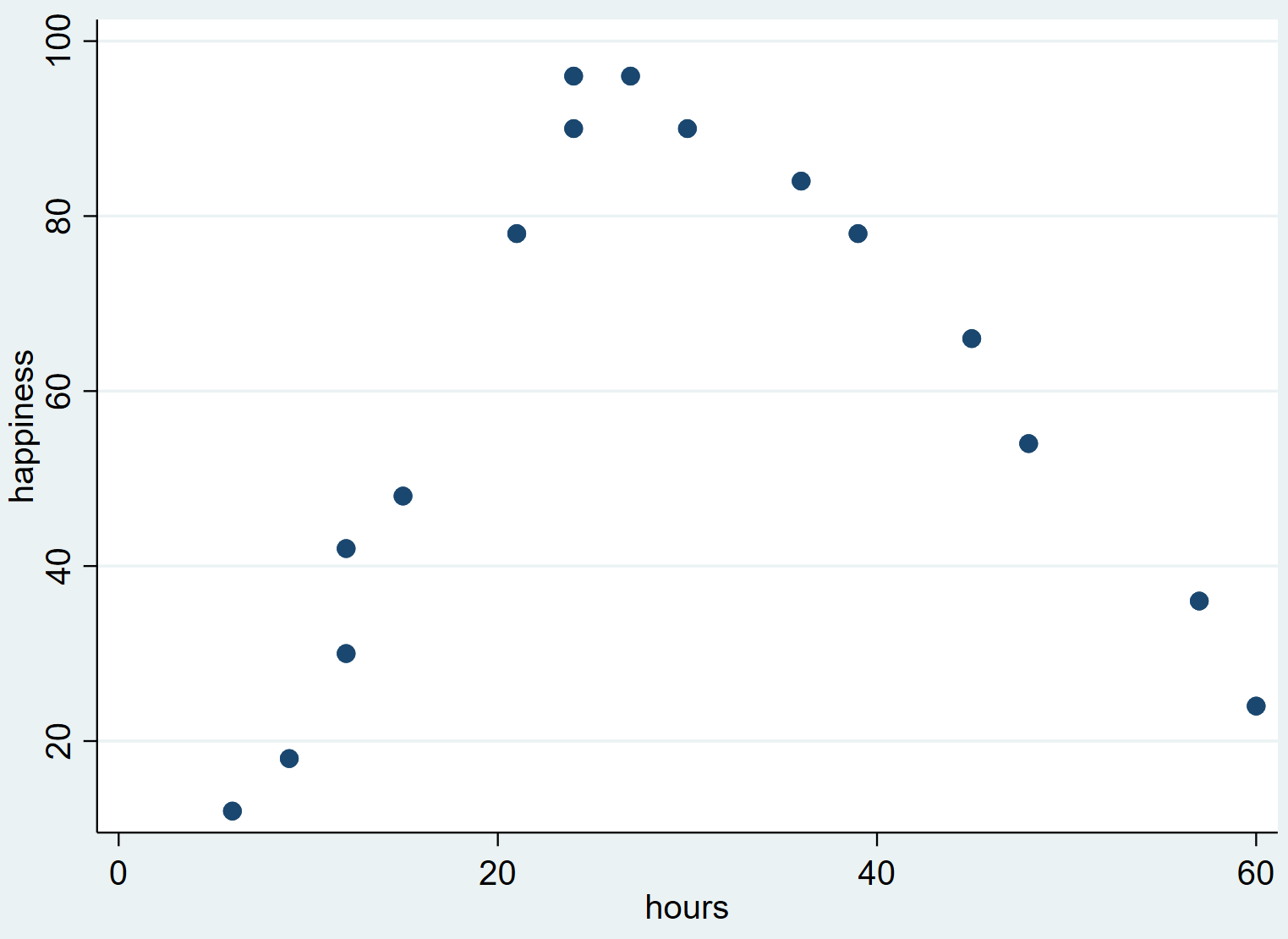
Мы видим, что счастье имеет тенденцию увеличиваться по мере того, как количество отработанных часов увеличивается от нуля до определенной точки, но затем начинает снижаться, когда количество отработанных часов превышает примерно 30.
Эта перевернутая буква «U» на диаграмме рассеяния указывает на то, что существует квадратичная зависимость между отработанными часами и счастьем, а это означает, что нам следует использовать квадратичную регрессию для количественной оценки этой зависимости.
Шаг 2: Выполните квадратичную регрессию.
Прежде чем подогнать модель квадратичной регрессии к данным, нам нужно создать новую переменную для квадратов значений нашей переменной-предиктора часов . Мы можем сделать это, введя следующее в поле «Команда»:
поколение часов2 = часы*часы
Мы можем просмотреть эту новую переменную, выбрав «Данные» > «Редактор данных» > «Редактор данных (обзор)» в верхнем меню.
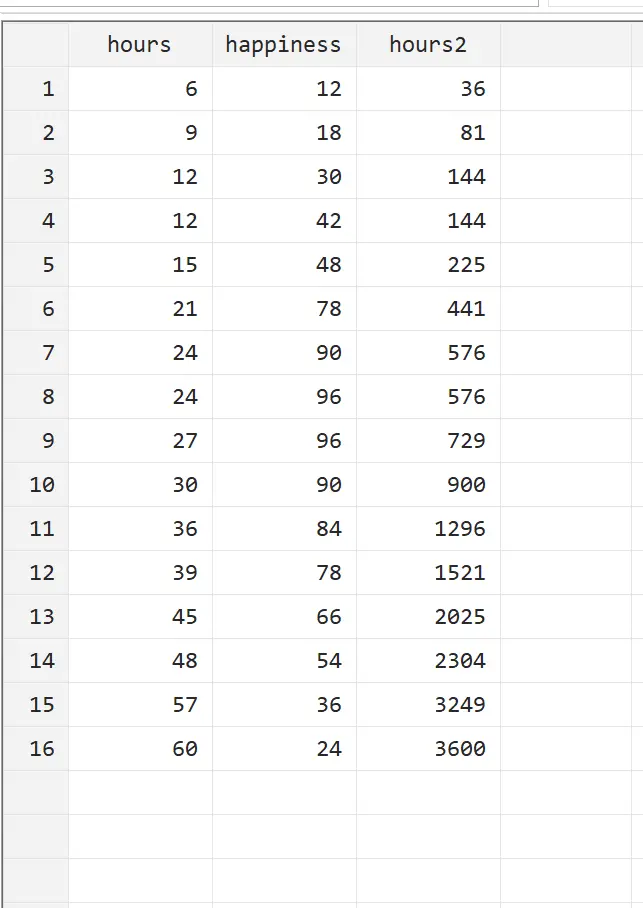
Мы видим, что часы2 — это просто часы в квадрате. Теперь мы можем выполнить квадратичную регрессию, используя часы и часы2 в качестве объясняющих переменных, а счастье — в качестве переменной отклика. Чтобы выполнить квадратичную регрессию, введите в поле «Команда» следующее:
регресс часы счастья часы2
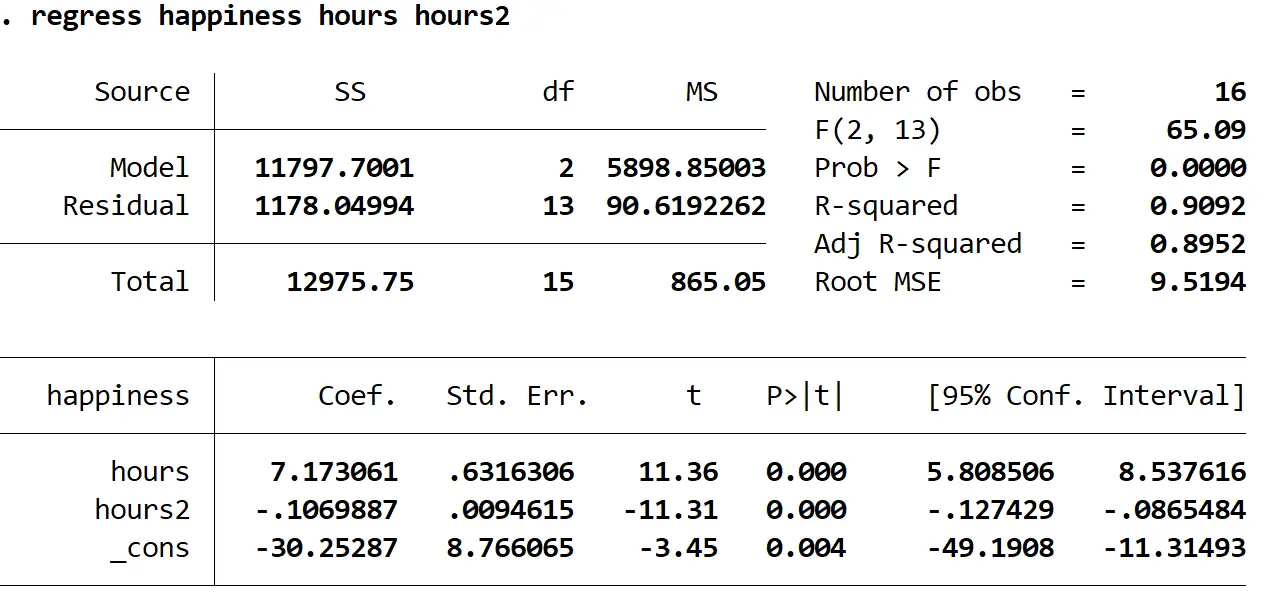
Вот как интерпретировать наиболее интересные цифры в результате:
Вероятность > F: 0,000. Это значение p для общей регрессии. Поскольку это значение меньше 0,05, это означает, что переменные-предикторы часы и часы 2 вместе взятые имеют статистически значимую связь с переменной ответа счастье .
R в квадрате: 0,9092. Это доля дисперсии переменной отклика, которую можно объяснить объясняющей переменной. В этом примере 90,92% изменений счастья можно объяснить часами 2 .
Уравнение регрессии: мы можем сформировать уравнение регрессии, используя значения коэффициентов, показанные в выходной таблице. В этом случае уравнение будет иметь вид:
прогнозируемое счастье = -30,25287 + 7,173061 (часы) – 0,1069887 ( 2 часа)
Мы можем использовать это уравнение, чтобы найти прогнозируемое счастье человека, учитывая количество часов, которые он работает в неделю.
Например, человек, который работает 60 часов в неделю, должен иметь уровень счастья 14,97:
прогнозируемое счастье = -30,25287 + 7,173061(60) – 0,1069887(60 2 ) = 14,97 .
И наоборот, человек, который работает 30 часов в неделю, должен иметь уровень счастья 88,65:
прогнозируемое счастье = -30,25287 + 7,173061(30) – 0,1069887(30 2 ) = 88,65 .
Шаг 3: Сообщите о результатах.
Наконец, мы хотим сообщить о результатах нашей квадратичной регрессии. Вот пример того, как это сделать:
Квадратичная регрессия была проведена для количественной оценки взаимосвязи между количеством часов, отработанных человеком, и соответствующим ему уровнем счастья (измеряется от 0 до 100). Для анализа была использована выборка из 16 человек.
Результаты показали, что существует статистически значимая связь между объясняющими переменными часы и часы 2 и переменной ответа счастье (F(2, 13) = 65,09, p <0,0001).
Вместе эти две объясняющие переменные составляют 90,92% объясняемой изменчивости счастья.
Уравнение регрессии оказалось таким:
прогнозируемое счастье = -30,25287 + 7,173061 (часы) – 0,1069887 ( 2 часа)