Тест фридмана: определение, формула и пример
Критерий Фридмана — это непараметрическая альтернатива дисперсионному анализу с повторными измерениями .
Он используется для определения того, существует ли статистически значимая разница между средними значениями трех или более групп, в которых одни и те же субъекты фигурируют в каждой группе.
Когда использовать тест Фридмана
Тест Фридмана обычно используется в двух ситуациях:
1. Измерьте средние баллы испытуемых за три или более временных интервала.
Например, вы можете измерить оставшуюся частоту сердечных сокращений субъектов за месяц до начала программы тренировок, через месяц после начала программы и через два месяца после ее использования. Вы можете выполнить тест Фридмана, чтобы увидеть, существует ли значительная разница в средней оставшейся частоте сердечных сокращений пациентов в эти три момента времени.
2. Измерьте средние баллы испытуемых в трех разных условиях.
Например, вы можете попросить испытуемых посмотреть три разных фильма и оценить каждый из них в зависимости от того, насколько он им понравился. Поскольку каждая тема присутствует в каждой выборке, вы можете запустить тест Фридмана, чтобы увидеть, существует ли значительная разница в среднем рейтинге трех фильмов.
Тест Фридмана: пример
Предположим, мы хотим знать, различается ли среднее время реакции испытуемых на три разных препарата. Чтобы проверить это, мы набираем 10 пациентов и измеряем время их реакции (в секундах) на три разных препарата. Результаты для каждого пациента представлены ниже:
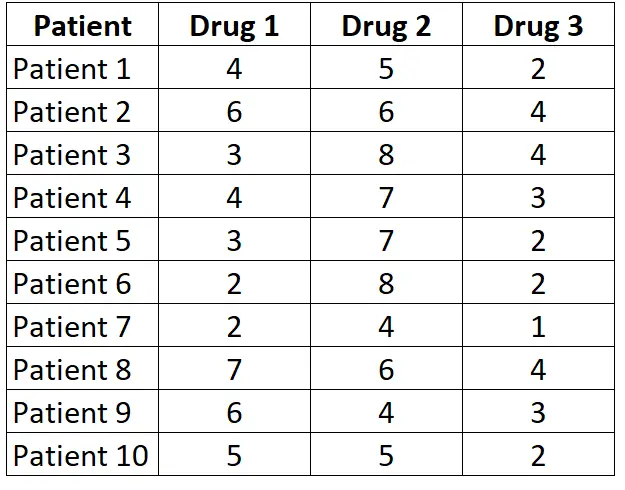
Поскольку у каждого пациента измеряется прием каждого из трех лекарств, мы будем использовать тест Фридмана, чтобы определить, различается ли среднее время реакции между тремя лекарствами.
Шаг 1. Сформулируйте гипотезы.
Нулевая гипотеза (H 0 ): µ 1 = µ 2 = µ 3 (среднее время реакции во всех популяциях одинаково)
Альтернативная гипотеза: (Ха): по крайней мере одно среднее значение генеральной совокупности отличается от остальных.
Шаг 2. Выполните тест Фридмана.
Мы будем использовать калькулятор теста Фридмана , используя следующие входные данные:
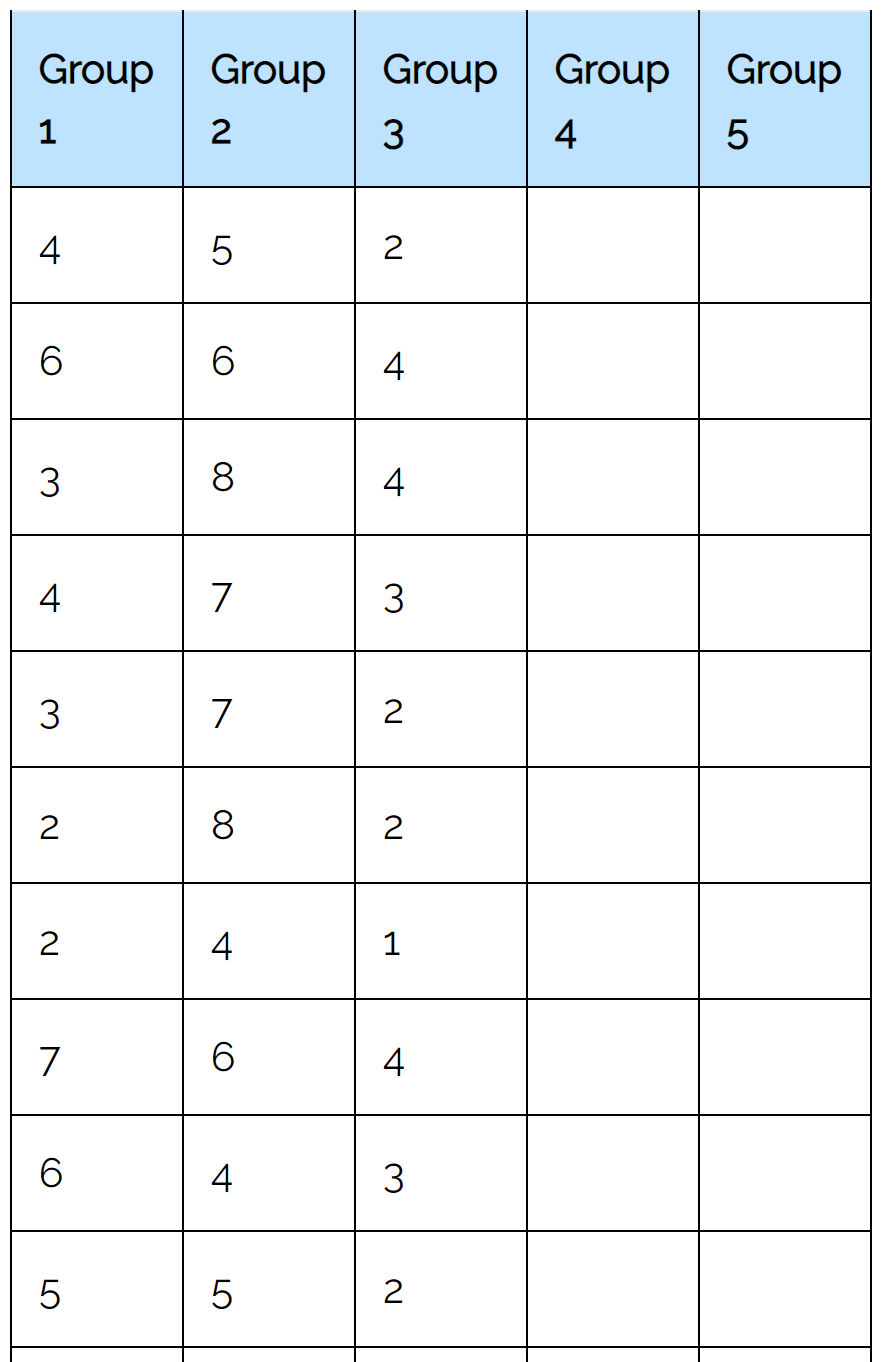
Как только мы нажмем «Рассчитать», автоматически появится следующий результат:

Шаг 3: Интерпретируйте результаты.
Статистика теста равна Q = 12,35 , а соответствующее значение p — p = 0,00208 . Поскольку это значение меньше 0,05, мы можем отвергнуть нулевую гипотезу о том, что среднее время ответа одинаково для всех трех препаратов.
У нас есть достаточно доказательств, чтобы сделать вывод, что тип используемого лекарства приводит к статистически значимым различиям во времени ответа.
Шаг 4: Сообщите о результатах.
Наконец, мы хотели бы сообщить о результатах испытаний. Вот пример того, как это сделать:
Тест Фридмана был проведен на 10 пациентах, чтобы изучить влияние трех различных лекарств на время ответа. Каждый пациент использовал каждый препарат один раз.
Результаты показали, что тип используемого лекарства приводил к статистически значимым различиям во времени ответа (Q = 12,35, p = 0,00208).
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнить тест Фридмана с использованием различного статистического программного обеспечения:
Как выполнить тест Фридмана в Excel
Как выполнить тест Фридмана в R
Как выполнить тест Фридмана в Python
Как выполнить тест Фридмана в Stata
Онлайн-калькулятор теста Фридмана