Ввод текста

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что значит характеризовать распределение в статистике. Таким образом, вы найдете определение типизации, пример типизации переменной и, кроме того, сможете попрактиковаться, решая пошагово упражнение.

Что такое печатать?

В статистике нормализация — это процесс, в котором линейное преобразование применяется к распределению так, что его среднее и стандартное отклонение равны нулю и единице соответственно.

Точнее, типирование предполагает вычитание среднего значения из случайной величины и последующее деление его на стандартное отклонение.

Типизацию также можно назвать нормализацией или стандартизацией.

Формула ввода

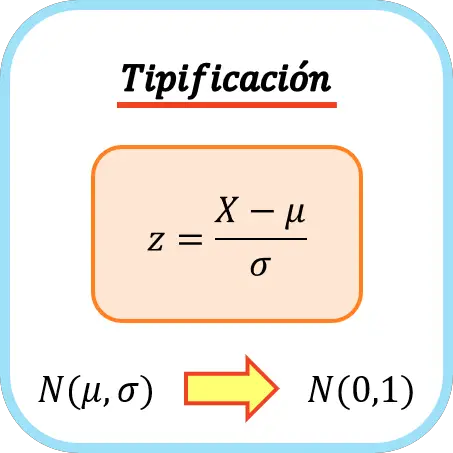
Чтобы классифицировать переменную, вы должны вычесть ее среднее значение, а затем разделить на стандартное отклонение. Таким образом, формула для ввода переменной выглядит следующим образом:

Золото

$\mu$

среднее значение переменной

$X$

$\sigma$

его стандартное отклонение (или стандартное отклонение).

Следовательно, запись фактически является изменением переменной, поскольку к переменной применяется линейное преобразование.

Пример записи

Учитывая определение типизации и ее формулу, ниже приведен конкретный пример для полного понимания этой концепции.

Непрерывная случайная величина подчиняется нормальному распределению со средним значением 45 и стандартным отклонением 10. Какова вероятность получить значение меньше или равное 60?

$N(45,10)$

Чтобы найти вероятность нормального распределения, нам нужно использовать таблицу его характеристик, но для этого нам нужно сначала выполнить процесс типизации. Поэтому мы вычитаем среднее значение и делим на стандартное отклонение значения вероятности:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

После того, как мы стандартизировали, мы переходим к таблице вероятностей нормального распределения, чтобы увидеть, какой вероятности соответствует значение 1,5:

Как видно из таблицы типизации нормального распределения, значение, рассчитанное на предыдущем шаге, соответствует следующей вероятности:

$\displaystyle P(Z\leq 1,5)=0,9332$

Таким образом, вероятность получения значения, равного или меньшего 60, составляет 93,32%.

Упражнение по набору текста решено

Рассчитайте следующие вероятности нормального распределения, среднее значение и стандартное отклонение которого равны 120 и 50 соответственно.

$N(120,50)$

Вероятность получения значения меньше или равного 208.
Вероятность получения значения больше 137.

Посмотреть решение

В обоих разделах задачи нам нужно ввести нормальное распределение для расчета вероятностей.

Начнем с расчета вероятностной типизации значения, меньшего или эквивалентного 208:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

А теперь посмотрим по таблице выше, какой вероятности соответствует значение 1,76:

$\displaystyle P(Z\leq 1,76)=0,9608$

Во-вторых, посчитаем вероятность получения значения больше 137. Точно так же начнем с ввода переменной:

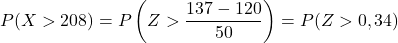$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)» title=»Rendered by QuickLaTeX.com» height=»43″ width=»398″ style=»vertical-align: -17px;»> <p class=$ Однако прикрепленная таблица имеет только самые низкие совокупные вероятности, поэтому, чтобы использовать таблицу, мы должны сначала преобразовать вероятность:

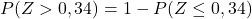$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)» title=»Rendered by QuickLaTeX.com» height=»19″ width=»252″ style=»vertical-align: -5px;»> <p class=$ И, наконец, отметим из прилагаемой таблицы вероятность, соответствующую расчетному значению Z:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=»Rendered by QuickLaTeX.com» height=»19″ width=»435″ style=»vertical-align: -5px;»> <div class=$

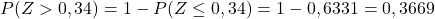
Какой смысл печатать?

Чтобы закончить понимание значения типизации, мы увидим, для чего она используется и когда необходимо типизировать переменную.

В основном стандартизация используется для сравнения значений распределений с разными средними и дисперсиями. Аналогично, стандартизация также используется для расчета вероятности.

Стандартизируя два значения распределений с разными характеристиками, мы можем увидеть, какое значение больше или меньше относительно всего распределения. Другими словами, применяя процесс типизации, мы можем увидеть, какое значение ближе или дальше всего от среднего значения его распределения.

Кроме того, как объяснялось выше, типизация также позволяет рассчитывать вероятности, поскольку обычно таблицы вероятностей основаны на типизированном распределении.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше