Центральная предельная теорема

В этой статье объясняется, что такое центральная предельная теорема (ЦПТ) и для чего она используется в статистике. Вы также узнаете, что представляет собой формула центральной предельной теоремы и пример ее применения, решенный шаг за шагом.

Что такое центральная предельная теорема?

В статистике центральная предельная теорема , также называемая центральной предельной теоремой , утверждает, что распределение выборочных средних приближается к нормальному распределению по мере увеличения размера выборки, независимо от вероятностного распределения населения.

То есть центральная предельная теорема гласит, что если мы возьмем достаточно большое количество выборок, среднее значение этих выборок можно приблизить к нормальному распределению.

Кроме того, центральная предельная теорема утверждает, что среднее значение выборки будет приближаться к значению среднего значения генеральной совокупности по мере увеличения размера выборки. Это позволяет аппроксимировать параметры статистической совокупности. Ниже мы увидим, как это делается.

В целом считается, что для применения центральной предельной теоремы размер выборки должен составлять не менее 30 наблюдений, хотя это зависит от характеристик изучаемой переменной.

Центральная предельная теорема имеет множество применений, поскольку нормальное распределение позволяет проводить статистические вычисления, такие как проверка гипотез или доверительные интервалы. Например, в финансах центральная предельная теорема используется для анализа доходности и риска инвестиций.

Пример центральной предельной теоремы

Разобравшись с определением центральной предельной теоремы, давайте рассмотрим пример, чтобы полностью понять ее смысл.

Примером центральной предельной теоремы является бросание игральной кости. Бросок кубика следует дискретному равномерному распределению , поскольку все исходы равновероятны. А вот распределение суммы нескольких результатов приближается к нормальному распределению.

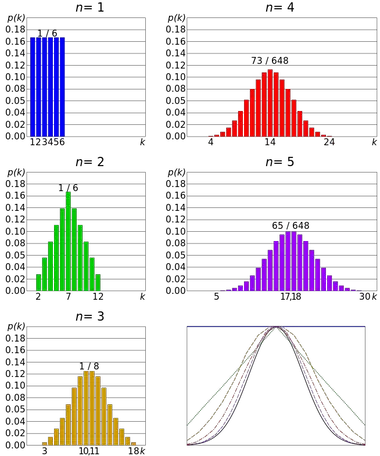
Таким образом, чем больше бросков, тем больше вероятность того, что форма распределения средних будет напоминать график нормального распределения.

Формула центральной предельной теоремы

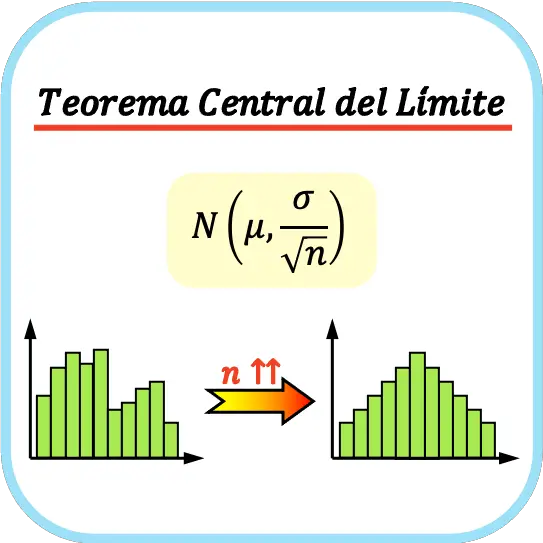
Центральная предельная теорема гласит, что если популяция имеет среднее значение µ и стандартное отклонение σ и мы берем достаточно большое количество выборок (n≥30), набор выборочных средних можно аппроксимировать к нормальному распределению со средним значением µ и стандартным отклонением σ. /√н.

Кроме того , _если X _{1 ,} к нормальному распределению, определяемому следующей формулой:

Решенное упражнение центральной предельной теоремы

Чтобы вы могли полностью усвоить эту концепцию, вот решенное упражнение центральной предельной теоремы.

• Компания продает детали, которые используются для замены определенных компонентов игрушек. Монета имеет средний вес 300 г и стандартное отклонение 50 г. Если покупатель заказал партию из 100 штук, какова вероятность того, что средний вес штук в партии будет больше 305 г? И какова вероятность того, что партия из 100 штук весит более 31 кг?

Поскольку размер партии велик (n=100), мы можем применить центральную предельную теорему для решения проблемы.

Таким образом, используя формулу центральной предельной теоремы, распределение выборочных средних можно приблизить к нормальному распределению со следующими параметрами:

Теперь мы выполняем процесс набора текста, чтобы затем найти вероятность, которую требует от нас упражнение. Для этого нам нужно вычесть среднее значение из распределения, а затем разделить на стандартное отклонение:

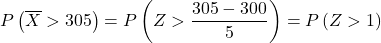таблица нормального распределения :

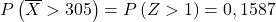
Итак, мы повторяем процесс набора текста, затем находим вторую вероятность, которую нам задает задача:

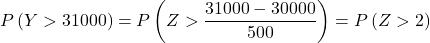
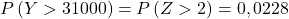➤ См.: Закон больших чисел.