Что означает, если статистика устойчива?

Статистика называется устойчивой, если она не чувствительна к экстремальным значениям.

Вот два примера устойчивой статистики:

• Медиана
• Межквартильный размах

Вот примеры статистики, которая не выдерживает критики:

• Среднее
• Стандартное отклонение
• Аккуратный

Следующий пример иллюстрирует разницу между устойчивой и неустойчивой статистикой.

Пример: статистика устойчивости и неустойчивости.

Предположим, у нас есть следующий набор данных:

Набор данных: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29.

Используя калькулятор или статистическое программное обеспечение, мы можем рассчитать значение следующей статистики холдингов для этого набора данных:

• Медиана: 13
• Межквартильный размах: 13,5

Мы также можем рассчитать значение следующей неустойчивой статистики для этого набора данных:

• Средний: 13,54
• Стандартное отклонение: 8,82
• Диапазон: 27

Теперь подумайте, был ли в этот набор данных добавлен экстремальный выброс:

Набор данных: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450.

Мы можем снова рассчитать значение следующей устойчивой статистики для этого набора данных:

• Медиана: 14
• Межквартильный размах: 15,75

Мы также можем рассчитать значение следующей неустойчивой статистики для этого набора данных:

• Средний: 49,92
• Стандартное отклонение: 126,27
• Диапазон: 448

Обратите внимание, насколько изменилась статистика несопротивления, если просто добавить к набору данных экстремальное значение:

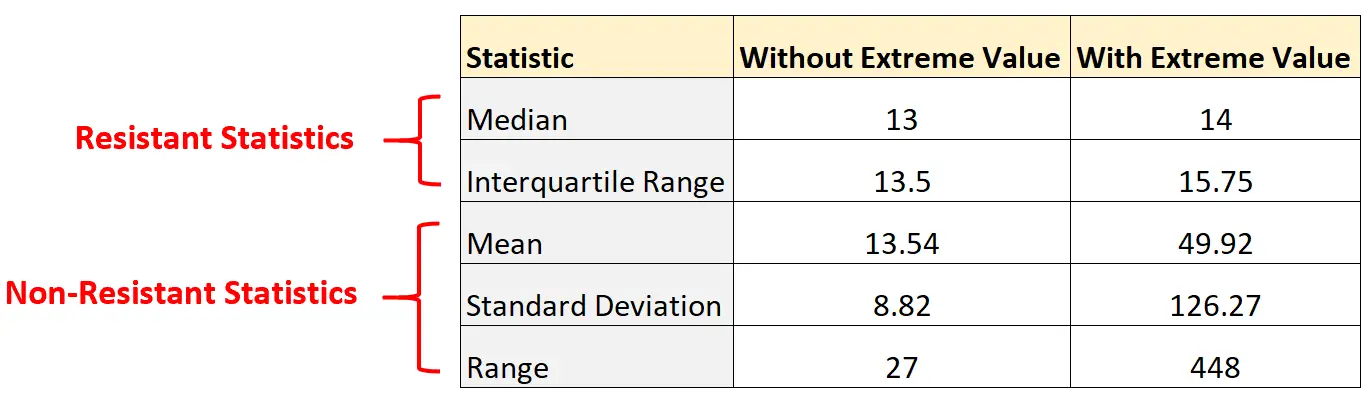
И наоборот, статистика бойцов сопротивления практически не изменилась. Медиана и межквартильный размах изменились незначительно.

Когда использовать устойчивую статистику

Наиболее часто используемые статистические данные для измерения центра и дисперсии значений в наборе данных — это среднее значение и стандартное отклонение соответственно.

К сожалению, обе эти статистики чувствительны к экстремальным значениям. Таким образом, если в наборе данных присутствуют выбросы, среднее и стандартное отклонение не будут точно описывать распределение значений в наборе данных.

Вместо этого рекомендуется использовать медиану и межквартильный размах для измерения центра и дисперсии значений в наборе данных, если присутствуют выбросы, поскольку обе эти статистики являются надежными .

Дополнительные ресурсы

Как выбросы влияют на среднее значение?
Когда использовать среднее значение, а не медиану
Когда использовать межквартильный размах или стандартное отклонение