Что такое бета-уровень в статистике? (определение & #038; пример)

В статистике мы используем проверку гипотез , чтобы определить, верна ли гипотеза о параметре совокупности .

Проверка гипотезы всегда предполагает наличие следующих двух гипотез:

Нулевая гипотеза (H ₀ ): данные выборки согласуются с доминирующим убеждением относительно параметра популяции.

Альтернативная гипотеза ( _HA ): данные выборки показывают, что гипотеза, изложенная в нулевой гипотезе, неверна. Другими словами, на данные влияет неслучайная причина.

Всякий раз, когда мы проводим проверку гипотезы, всегда есть четыре возможных результата:

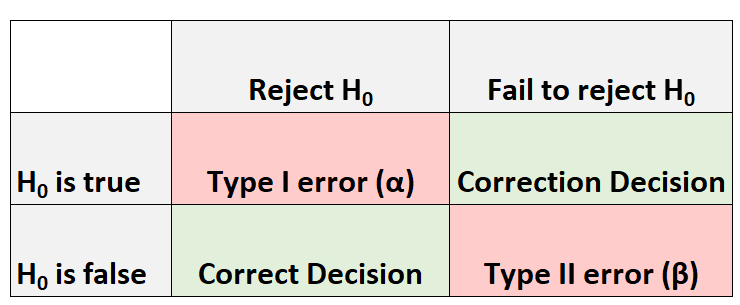
Мы можем допустить два типа ошибок:

• Ошибка I рода: мы отвергаем нулевую гипотезу, когда она на самом деле верна. Вероятность совершения ошибки этого типа обозначается α .
• Ошибка второго рода: мы не можем отвергнуть нулевую гипотезу, когда она на самом деле ложна. Вероятность совершения этого типа ошибки обозначается β .

Связь между альфой и бета

В идеале исследователи хотят, чтобы вероятность совершения ошибки типа I и вероятность совершения ошибки типа II была низкой.

Однако между этими двумя вероятностями существует компромисс. Если мы уменьшим уровень альфа, мы можем уменьшить вероятность отклонения нулевой гипотезы, когда она на самом деле верна, но на самом деле это увеличивает уровень бета – вероятность того, что нам не удастся отвергнуть нулевую гипотезу, когда она неверна.

Связь между мощностью и бета

Сила проверки гипотезы означает вероятность обнаружения эффекта или различия, когда эффект или различие действительно присутствуют. Другими словами, это вероятность правильно отвергнуть ложную нулевую гипотезу.

Он рассчитывается следующим образом:

Мощность = 1 – β

В общем, исследователи хотят, чтобы мощность теста была высокой, чтобы, если есть эффект или разница, тест мог его обнаружить.

Из приведенного выше уравнения мы видим, что лучший способ повысить эффективность теста — снизить уровень бета. И лучший способ снизить уровень бета — обычно увеличить размер выборки.

В следующих примерах показано, как рассчитать уровень бета для проверки гипотезы, и показано, почему увеличение размера выборки может снизить уровень бета.

Пример 1. Вычисление бета для проверки гипотезы

Предположим, исследователь хочет проверить, составляет ли средний вес изделий, производимых на фабрике, менее 500 унций. Мы знаем, что стандартное отклонение весов составляет 24 унции, и исследователь решает собрать случайную выборку из 40 виджетов.

При α = 0,05 будет реализована следующая гипотеза:

• Ч ₀ : µ = 500
• H _A : мкм < 500

Теперь представьте, что средний вес производимых изделий на самом деле составляет 490 унций. Другими словами, нулевая гипотеза должна быть отвергнута.

Мы можем использовать следующие шаги для расчета бета-уровня – вероятности не отвергнуть нулевую гипотезу, хотя на самом деле ее следует отвергнуть:

Шаг 1: Найдите область без отклонения.

Согласно калькулятору критического значения Z, левое критическое значение при α = 0,05 составляет -1,645 .

Шаг 2. Найдите минимальную выборку, которую мы не сможем отклонить.

Статистика теста рассчитывается как z = ( x – µ) / (s/ √n )

Итак, мы можем решить это уравнение для выборочного среднего:

• x = µ – z*(s/ √n )
• х = 500 – 1,645*(24/ √40 )
• х = 493,758

Шаг 3: Определите вероятность того, что минимальное выборочное среднее действительно будет достигнуто.

Эту вероятность мы можем вычислить следующим образом:

• P(Z ≥ (493,758 – 490) / (24/√ 40 ))
• П(З ≥ 0,99)

Согласно обычному калькулятору CDF , вероятность того, что Z ≥ 0,99, равна 0,1611 .

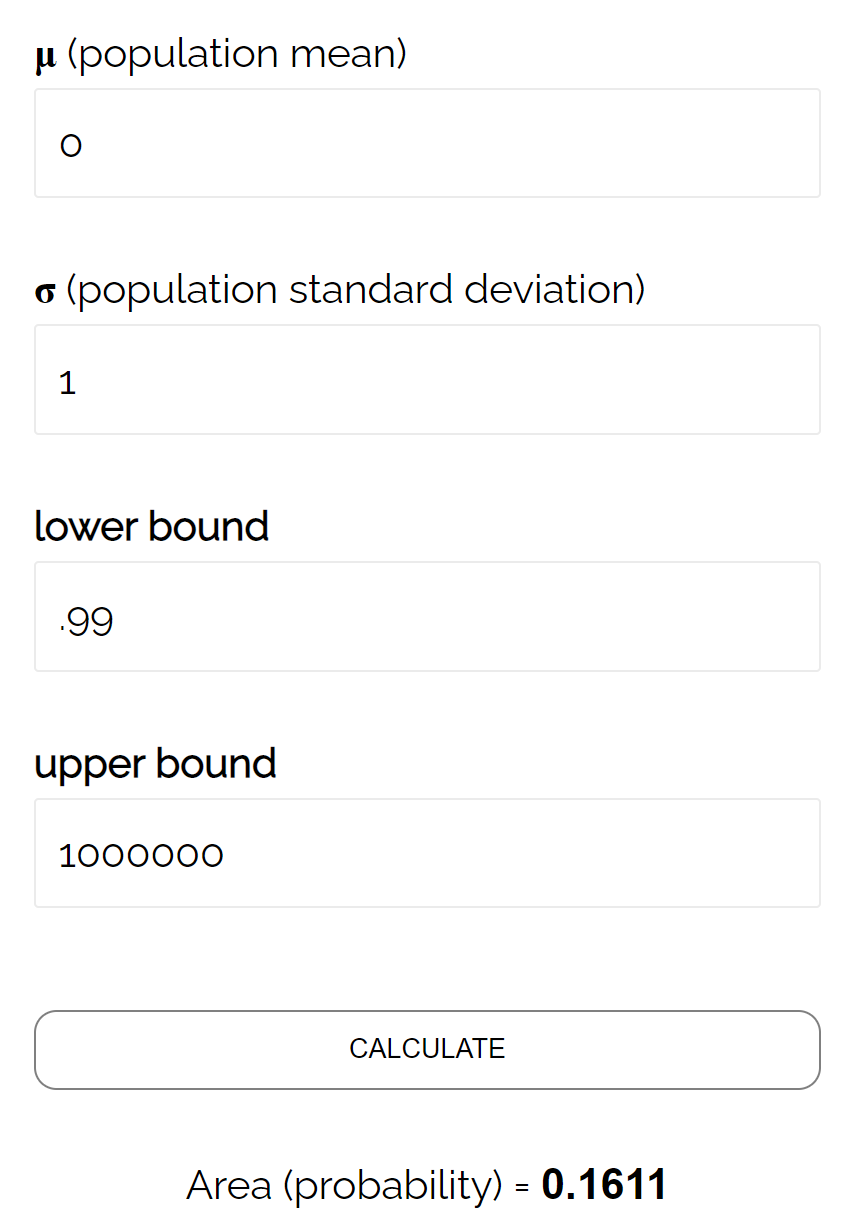
Таким образом, уровень бета для этого теста составляет β = 0,1611. Это означает, что существует вероятность 16,11% не обнаружить разницу, если фактическое среднее значение составляет 490 унций.

Пример 2. Вычисление бета для теста с большим размером выборки

Теперь предположим, что исследователь выполняет ту же самую проверку гипотезы, но вместо этого использует выборку из n = 100 виджетов. Мы можем повторить те же три шага, чтобы вычислить уровень бета для этого теста:

Шаг 1: Найдите область без отклонения.

Согласно калькулятору критического значения Z, левое критическое значение при α = 0,05 составляет -1,645 .

Шаг 2. Найдите минимальную выборку, которую мы не сможем отклонить.

Статистика теста рассчитывается как z = ( x – µ) / (s/ √n )

Итак, мы можем решить это уравнение для выборочного среднего:

• x = µ – z*(s/ √n )
• х = 500 – 1,645*(24/√ 100 )
• х = 496,05

Шаг 3: Определите вероятность того, что минимальное выборочное среднее действительно будет достигнуто.

Эту вероятность мы можем вычислить следующим образом:

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• П(Z ≥ 2,52)

Согласно обычному калькулятору CDF , вероятность того, что Z ≥ 2,52, равна 0,0059.

Таким образом, уровень бета для этого теста составляет β = 0,0059. Это означает, что существует только 0,59% шанс не обнаружить разницу, если фактическое среднее значение составляет 490 унций.

Обратите внимание: просто увеличив размер выборки с 40 до 100, исследователь смог снизить уровень бета с 0,1611 до 0,0059.

Бонус: используйте этот калькулятор ошибок второго рода для автоматического расчета бета-уровня теста.

Дополнительные ресурсы

Введение в проверку гипотез
Как написать нулевую гипотезу (5 примеров)
Объяснение значений P и статистической значимости