Виды асимметрии

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье вы узнаете, сколько видов асимметрии существует в статистике. Таким образом, каждый вид асимметрии поясняется на примерах, а кроме того, вы сможете увидеть, как рассчитывается асимметрия распределения.

Какие бывают виды асимметрии?

В статистике различают три типа асимметрии :

Положительная асимметрия : распределение имеет больше разных значений справа от среднего значения, чем слева.
Отрицательная асимметрия : распределение имеет больше разных значений слева от среднего значения, чем справа.
Симметрия : распределение имеет одинаковое количество значений слева и справа от среднего значения.

Каждый тип асимметрии объясняется более подробно ниже.

положительная асимметрия

Когда распределение имеет положительную асимметрию , это означает, что правый хвост его графика длиннее левого. То есть распределение имеет больше разных значений справа от среднего.

Кривая в предыдущем примере положительно асимметрична, поскольку справа от среднего значения гораздо больше значений, чем слева. Как вы можете видеть на графике, полоса, показанная зеленым цветом, намного больше, чем оранжевая полоса.

негативная асимметрия

В статистике распределение называется отрицательным , если его график имеет левый хвост длиннее правого. То есть отрицательно перекошенное распределение означает, что оно имеет больше разных значений слева от среднего значения.

Если вы посмотрите на предыдущий график, то слева от среднего значения больше, чем справа, поэтому кривая имеет отрицательный перекос.

Симметрия

Распределение является симметричным , когда количество значений слева от среднего равно количеству значений справа от среднего. Таким образом, среднее значение действует как ось симметрии.

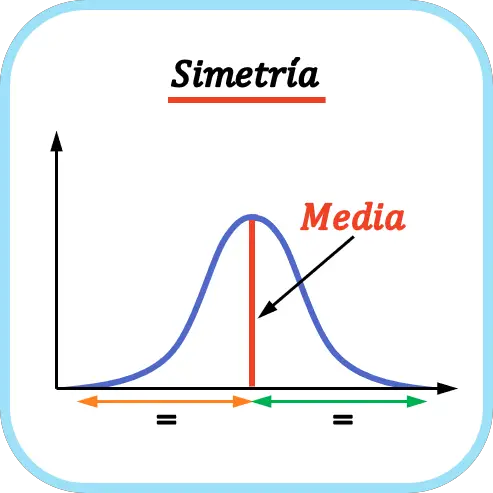
Как показано в примере выше, количество значений слева от среднего значения представленного распределения вероятностей совпадает с количеством значений справа от среднего, поэтому это симметричное распределение.

Как определить тип асимметрии

Теперь, когда мы знаем, какие типы асимметрии существуют в статистике, давайте посмотрим, как узнать, какому типу асимметрии соответствует распределение вероятностей.

Традиционно объясняют, что мы можем узнать тип асимметрии распределения на основе соотношения между его средним значением и медианой (независимо от того, больше оно, эквивалентно или меньше). Однако это свойство не всегда выполняется. Таким образом, чтобы определить асимметрию распределения, необходимо рассчитать коэффициент асимметрии Фишера.

Коэффициент асимметрии Фишера рассчитывается по следующей формуле:

$\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]$

Или эквивалент:

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}$

Золото

$E$

это математическое ожидание ,

$\mu$

среднее арифметическое и

$\sigma$

стандартное отклонение .

И как только коэффициент Фишера рассчитан, его знак позволяет определить, какой тип асимметрии представляет собой распределение:

Если коэффициент асимметрии Фишера положителен, распределение асимметрично положительно.
Если коэффициент асимметрии Фишера отрицательный, распределение искажено отрицательно.
Если распределение симметрично, коэффициент асимметрии Фишера равен нулю (обратное не всегда верно).

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше